We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We show that if there is a supercompact cardinal, then Keisler’s order is not linear. More specifically, let Tn,k be the theory of the generic n-clique free k-ary graph for any n > k ≥ 3, and let TCas be the simple nonlow theory described by Casanovas in [2]. Then we show that TCas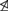
$$Tn,k always, and if there is a supercompact cardinal then Tn,k
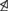$$TCas.
We show there exists a complete theory in a language of size continuum possessing a unique atomic model which is not constructible. We also show it is consistent with 
$ZFC + {\aleph _1} < {2^{{\aleph _0}}}$ that there is a complete theory in a language of size 
${\aleph _1}$ possessing a unique atomic model which is not constructible. Finally we show it is consistent with 
$ZFC + {\aleph _1} < {2^{{\aleph _0}}}$ that for every complete theory T in a language of size 
${\aleph _1}$, if T has uncountable atomic models but no constructible models, then T has 
${2^{{\aleph _1}}}$ atomic models of size 
${\aleph _1}$.
