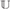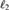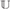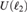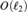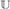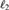1 results
CONSEQUENCES OF THE EXISTENCE OF AMPLE GENERICS AND AUTOMORPHISM GROUPS OF HOMOGENEOUS METRIC STRUCTURES
-
- Journal:
- The Journal of Symbolic Logic / Volume 81 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 14 September 2016, pp. 876-886
- Print publication:
- September 2016
-
- Article
- Export citation
-
We define a simple criterion for a homogeneous, complete metric structure X that implies that the automorphism group Aut(X) satisfies all the main consequences of the existence of ample generics: it has the automatic continuity property, the small index property, and uncountable cofinality for nonopen subgroups. Then we verify it for the Urysohn space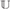
$$, the Lebesgue probability measure algebra MALG, and the Hilbert space 
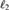$\ell _2 $, thus proving that Iso(
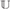$$), Aut(MALG), 
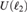$U\left( {\ell _2 } \right)$, and 
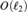$O\left( {\ell _2 } \right)$ share these properties. We also formulate a condition for X which implies that every homomorphism of Aut(X) into a separable group K with a left-invariant, complete metric, is trivial, and we verify it for 
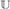$$, and 
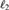$\ell _2 $.
