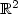1 results
Diffusion and propagation problems in some ramified domains with a fractal boundary
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 4 / July 2006
- Published online by Cambridge University Press:
- 15 November 2006, pp. 623-652
- Print publication:
- July 2006
-
- Article
- Export citation
-
This paper is devoted to some elliptic boundary value problems in a self-similar ramified domain of ${\mathbb R}^2$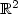
with a fractal boundary. Both the Laplace and Helmholtz equations are studied. A generalized Neumann boundary condition is imposed on the fractal boundary.Sobolev spaces on this domain are studied. In particular, extension and trace results are obtained. These results enable the investigation of the variational formulation of the above mentioned boundary value problems. Next, for homogeneous Neumann conditions, the emphasis is placed on transparent boundary conditions, which allow the computationof the solutions in the subdomains obtained by stopping the geometric construction after a finite number of steps. The proposed methods and algorithmswill be used numerically in forecoming papers.
