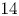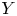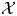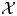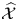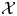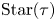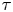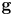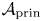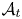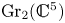We explain how to form a novel dataset of Calabi–Yau threefolds via the Gross–Siebert algorithm. We expect these to degenerate to Calabi–Yau toric hypersurfaces with certain Gorenstein (not necessarily isolated) singularities. In particular, we explain how to ‘smooth the boundary’ of a class of four-dimensional reflexive polytopes to obtain polarised tropical manifolds. We compute topological invariants of a compactified torus fibration over each such tropical manifold, expected to be homeomorphic to the general fibre of the Gross–Siebert smoothing. We consider a family of examples related to products of reflexive polygons. Among these we find $14$ topological types with $b_2=1$ that do not appear in existing lists of known rank-one Calabi–Yau threefolds.

We introduce the notion of a 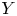$Y$-pattern with coefficients and its geometric counterpart: an 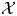$\mathcal {X}$-cluster variety with coefficients. We use these constructions to build a flat degeneration of every skew-symmetrizable specially completed 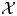$\mathcal {X}$-cluster variety 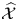$\widehat {\mathcal {X} }$ to the toric variety associated to its g-fan. Moreover, we show that the fibers of this family are stratified in a natural way, with strata the specially completed 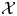$\mathcal {X}$-varieties encoded by 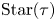$\operatorname {Star}(\tau )$ for each cone 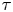$\tau$ of the 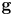$\mathbf {g}$-fan. These strata degenerate to the associated toric strata of the central fiber. We further show that the family is cluster dual to 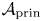$\mathcal {A}_{\mathrm {prin}}$ of Gross, Hacking, Keel and Kontsevich [Canonical bases for cluster algebras, J. Amer. Math. Soc. 31 (2018), 497–608], and the fibers cluster dual to 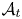$\mathcal {A} _t$. Finally, we give two applications. First, we use our construction to identify the toric degeneration of Grassmannians from Rietsch and Williams [Newton-Okounkov bodies, cluster duality, and mirror symmetry for Grassmannians, Duke Math. J. 168 (2019), 3437–3527] with the Gross–Hacking–Keel–Kontsevich degeneration in the case of 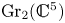$\operatorname {Gr}_2(\mathbb {C} ^{5})$. Next, we use it to link cluster duality to Batyrev–Borisov duality of Gorenstein toric Fanos in the context of mirror symmetry.