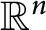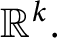A tight frame is the orthogonal projection of some orthonormal basis of $\mathbb {R}^n$ onto $\mathbb {R}^k.$ We show that a set of vectors is a tight frame if and only if the set of all cross products of these vectors is a tight frame. We reformulate a range of problems on the volume of projections (or sections) of regular polytopes in terms of tight frames and write a first-order necessary condition for local extrema of these problems. As applications, we prove new results for the problem of maximization of the volume of zonotopes.

This paper addresses the problem of how to restore degraded images where the pixels have been partly lost during transmission or damaged by impulsive noise. A wide range of image restoration tasks is covered in the mathematical model considered in this paper - e.g. image deblurring, image inpainting and super-resolution imaging. Based on the assumption that natural images are likely to have a sparse representation in a wavelet tight frame domain, we propose a regularization-based approach to recover degraded images, by enforcing the analysis-based sparsity prior of images in a tight frame domain. The resulting minimization problem can be solved efficiently by the split Bregman method. Numerical experiments on various image restoration tasks - simultaneously image deblurring and inpainting, super-resolution imaging and image deblurring under impulsive noise - demonstrated the effectiveness of our proposed algorithm. It proved robust to mis-detection errors of missing or damaged pixels, and compared favorably to existing algorithms.