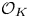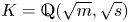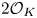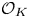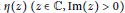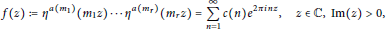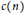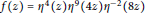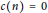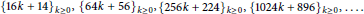We study totally positive definite quadratic forms over the ring of integers $\mathcal {O}_K$ of a totally real biquadratic field $K=\mathbb {Q}(\sqrt {m}, \sqrt {s})$. We restrict our attention to classic forms (i.e. those with all non-diagonal coefficients in $2\mathcal {O}_K$) and prove that no such forms in three variables are universal (i.e. represent all totally positive elements of $\mathcal {O}_K$). Moreover, we show the same result for totally real number fields containing at least one non-square totally positive unit and satisfying some other mild conditions. These results provide further evidence towards Kitaoka's conjecture that there are only finitely many number fields over which such forms exist. One of our main tools are additively indecomposable elements of $\mathcal {O}_K$; we prove several new results about their properties.

Let 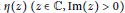$\eta \left( z \right)\,\left( z\,\in \,\mathbb{C},\,\operatorname{Im}\left( z \right)\,>\,0 \right)$ denote the Dedekind eta function. We use a recent product-to-sum formula in conjunction with conditions for the non-representability of integers by certain ternary quadratic forms to give explicitly ten eta quotients

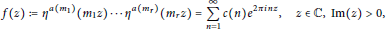$$f\left( z \right)\,:=\,{{\eta }^{a\left( {{m}_{1}} \right)}}\,\left( {{m}_{1}}z \right)\,.\,.\,.\,{{\eta }^{a\left( {{m}_{r}} \right)}}\,\left( {{m}_{r}}z \right)\,=\,\sum\limits_{n=1}^{\infty }{c\left( n \right){{e}^{2\pi inz}},\,\,\,z\,\in \,\mathbb{C},\,\operatorname{Im}\left( z \right)\,>\,0,}$$

such that the Fourier coefficients 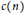$c\left( n \right)$ vanish for all positive integers $n$ in each of infinitely many non-overlapping arithmetic progressions. For example, we show that if 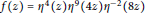$f\left( z \right)\,=\,{{\eta }^{4}}\left( z \right){{\eta }^{9}}\left( 4z \right){{\eta }^{-2}}\left( 8z \right)$ we have 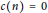$c\left( n \right)\,=\,0$ for all $n$ in each of the arithmetic progressions 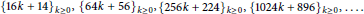${{\{16k\,+\,14\}}_{k\ge 0}},\,{{\{64k\,+\,56\}}_{k\ge 0}},\,{{\{256k,\,224\}}_{k\ge 0}},\,{{\{1024k\,+\,869\}}_{k\ge 0}},\,.\,.\,.$