The game 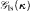 is played on a complete Boolean algebra
is played on a complete Boolean algebra  , by two players. White and Black, in κ-many moves (where κ is an infinite cardinal). At the beginning White chooses a non-zero element p ∈
, by two players. White and Black, in κ-many moves (where κ is an infinite cardinal). At the beginning White chooses a non-zero element p ∈  . In the α-th move White chooses pα ∈ (0, p)
. In the α-th move White chooses pα ∈ (0, p) and Black responds choosing iα ∈{0, 1}. White winsthe play iff
and Black responds choosing iα ∈{0, 1}. White winsthe play iff 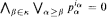 . where
. where 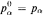 and
and 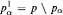 .
.
The corresponding game theoretic properties of c.B.a.'s are investigated. So, Black has a winning strategy (w.s.) if κ ≥ π( ) or if
) or if  contains a κ-closed dense subset. On the other hand, if White has a w.s., then κ ∈
contains a κ-closed dense subset. On the other hand, if White has a w.s., then κ ∈ 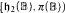 . The existence of w.s. is characterized in a combinatorial way and in terms of forcing. In particular, if 2<κ = κ ∈ Reg and forcing by
. The existence of w.s. is characterized in a combinatorial way and in terms of forcing. In particular, if 2<κ = κ ∈ Reg and forcing by  preserves the regularity of κ, then White has a w.s. iff the power 2κ is collapsed to κ in some extension. It is shown that, under the GCH, for each set S ⊆ Reg there is a c.B.a.
preserves the regularity of κ, then White has a w.s. iff the power 2κ is collapsed to κ in some extension. It is shown that, under the GCH, for each set S ⊆ Reg there is a c.B.a.  such that White (respectively. Black) has a w.s. for each infinite cardinal κ ∈ S (resp. κ ∉ S). Also it is shown consistent that for each κ ∈ Reg there is a c.B.a. on which the game
such that White (respectively. Black) has a w.s. for each infinite cardinal κ ∈ S (resp. κ ∉ S). Also it is shown consistent that for each κ ∈ Reg there is a c.B.a. on which the game 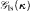 is undetermined.
is undetermined.

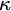
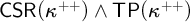
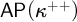
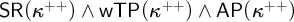
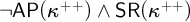
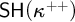
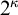
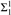
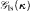 is played on a complete Boolean algebra
is played on a complete Boolean algebra  , by two players. White and Black, in
, by two players. White and Black, in 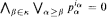 . where
. where 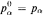 and
and 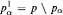 .
.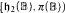 . The existence of w.s. is characterized in a combinatorial way and in terms of forcing. In particular, if 2
. The existence of w.s. is characterized in a combinatorial way and in terms of forcing. In particular, if 2