1 results
Infection Spread in Random Geometric Graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 04 January 2016, pp. 164-181
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
-
In this paper we study the speed of infection spread and the survival of the contact process in the random geometric graph G = G(n, rn, f) of n nodes independently distributed in S = [-½, ½]2 according to a certain density f(·). In the first part of the paper we assume that infection spreads from one node to another at unit rate and that infected nodes stay in the same state forever. We provide an explicit lower bound on the speed of infection spread and prove that infection spreads in G with speed at least D1nrn2. In the second part of the paper we consider the contact process ξt on G where infection spreads at rate λ > 0 from one node to another and each node independently recovers at unit rate. We prove that, for every λ > 0, with high probability, the contact process on G survives for an exponentially long time; there exist positive constants c1 and c2 such that, with probability at least 1 - c1 / n4, the contact process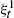
starting with all nodes infected survives up to time tn = exp(c2n/logn) for all n.
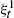starting with all nodes infected survives up to time 