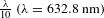1 results
Mechanistic study of continuous polishing
- Part of
-
- Journal:
- High Power Laser Science and Engineering / Volume 3 / 2015
- Published online by Cambridge University Press:
- 21 May 2015, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
To establish the mechanism of surface change in a continuous polishing system, an ideal mathematical model is built based on Winkler’s hypothesis and the Preston equation. The basic features of the model are the change rates in the surface peak–valley (PV) values of the workpiece, conditioning disk and pitch lap, rather than the specific surface shapes. In addition, an equilibrium state exists in the system, indicating that the surface change rates are all zero. Under equilibrium, the surface of the lap could remain flat, and it is insensitive to the surface error of the workpiece. These characteristics lay the theoretical foundations for high-efficiency and high-precision polishing. The methods to obtain an equilibrium state with flat surfaces are then proposed and confirmed experimentally. High-precision surfaces better than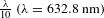
$\frac{{\it\lambda}}{10}~({\it\lambda}=632.8~\text{nm})$ are consistently produced experimentally.
