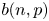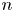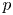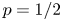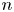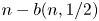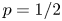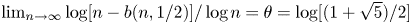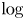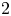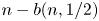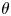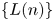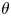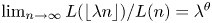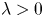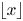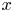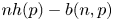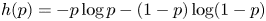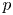von Neumann [(1951). Various techniques used in connection with random digits. National Bureau of Standards Applied Math Series 12: 36–38] introduced a simple algorithm for generating independent unbiased random bits by tossing a (possibly) biased coin with unknown bias. While his algorithm fails to attain the entropy bound, Peres [(1992). Iterating von Neumann's procedure for extracting random bits. The Annals of Statistics 20(1): 590–597] showed that the entropy bound can be attained asymptotically by iterating von Neumann's algorithm. Let $b(n,p)$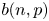 denote the expected number of unbiased bits generated when Peres’ algorithm is applied to an input sequence consisting of the outcomes of $n$ 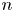tosses of the coin with bias $p$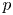. With $p=1/2$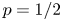, the coin is unbiased and the input sequence consists of $n$ 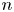unbiased bits, so that $n-b(n,1/2)$ 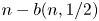may be referred to as the cost incurred by Peres’ algorithm when not knowing $p=1/2$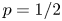. We show that $\lim _{n\to \infty }\log [n-b(n,1/2)]/\log n =\theta =\log [(1+\sqrt {5})/2]$ 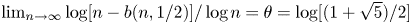(where $\log$ 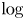is the logarithm to base $2$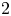), which together with limited numerical results suggests that $n-b(n,1/2)$ 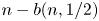may be a regularly varying sequence of index $\theta$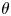. (A positive sequence $\{L(n)\}$ 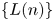is said to be regularly varying of index $\theta$ 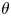if $\lim _{n\to \infty }L(\lfloor \lambda n\rfloor )/L(n)=\lambda ^\theta$ 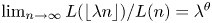for all $\lambda > 0$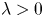, where $\lfloor x\rfloor$ 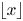denotes the largest integer not exceeding $x$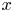.) Some open problems on the asymptotic behavior of $nh(p)-b(n,p)$ 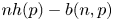are briefly discussed where $h(p)=-p\log p- (1-p)\log (1-p)$ 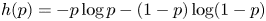denotes the Shannon entropy of a random bit with bias $p$.

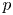In this paper we establish operator quasilinearity properties of some functionals associated with Davis–Choi–Jensen’s inequality for positive maps and operator convex or concave functions. Applications for the power function and the logarithm are provided.

The superadditivity and subadditivity of some functionals associated with the Riemann–Stieltjes integral are established. Applications in connection to Ostrowski’s and the generalized trapezoidal inequalities and for special means are provided.

In this paper a unified derivation of the upper and lower bounds (in terms of the mean) of an IFR, DFR, IFRA, DFRA, NBU or NWU reliability function is presented. The method of proof provides a simpler alternative to the various proofs known in the literature. Moreover, this method can be used to generalize the existing results in two ways, as demonstrated here. First, the bounds for the reliability function are obtained in terms of any finite moment in all these cases. Subsequently we provide a moment bound on a reliability function which ages faster or slower than a known one in some sense. The existing literature does not offer any of these generalizations, except for a few results which are available in an unnecessarily complicated form.