We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We provide the reader with a uniform approach for obtaining various useful explicit upper bounds on residues of Dedekind zeta functions of numbers fields and on absolute values of values at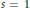 
$s=1$ of 
$L$-series associated with primitive characters on ray class groups of number fields. To make it quite clear to the reader how useful such bounds are when dealing with class number problems for CM-fields, we deduce an upper bound for the root discriminants of the normal CM-fields with (relative) class number one.
