In this paper, we develop the theory of singular Hermitian metrics on vector bundles. As an application, we give a structure theorem of a projective manifold X with pseudo-effective tangent bundle; X admits a smooth fibration 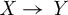$X \to Y$ to a flat projective manifold Y such that its general fibre is rationally connected. Moreover, by applying this structure theorem, we classify all the minimal surfaces with pseudo-effective tangent bundle and study general nonminimal surfaces, which provide examples of (possibly singular) positively curved tangent bundles.

We prove that every curve on a separably rationally connected variety is rationally equivalent to a (non-effective) integral sum of rational curves. That is, the Chow group of 1-cycles is generated by rational curves. Applying the same technique, we also show that the Chow group of 1-cycles on a separably rationally connected Fano complete intersection of index at least 2 is generated by lines. As a consequence, we give a positive answer to a question of Professor Totaro about integral Hodge classes on rationally connected 3-folds. And by a result of Professor Voisin, the general case is a consequence of the Tate conjecture for surfaces over finite fields.