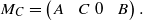An operator A on a complex, separable, infinite-dimensional Hilbert space H is hypercyclic if there is a vector x∈H such that the orbit {x,Ax,A2x,…} is dense in H. Using the character of the analytic core and quasinilpotent part of an operator A, we explore the hypercyclicity for upper triangular operator matrix