1 results
Quantum Families of Invertible Maps and Related Problems
-
- Journal:
- Canadian Journal of Mathematics / Volume 68 / Issue 3 / 01 June 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 698-720
- Print publication:
- 01 June 2016
-
- Article
-
- You have access
- Export citation
-
The notion of families of quantum invertible maps (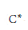
${{C}^{*}}$-algebra homomorphisms satisfying Podleś condition) is employed to strengthen and reinterpret several results concerning universal quantum groups acting on finite quantum spaces. In particular, Wang's quantum automorphism groups are shown to be universal with respect to quantum families of invertible maps. Further, the construction of the Hopf image of Banica and Bichon is phrased in purely analytic language and employed to define the quantum subgroup generated by a family of quantum subgroups or, more generally, a family of quantum invertible maps.
