A discrete time stochastic model for a multiagent system given in terms of a large collection of interacting Markov chains is studied. The evolution of the interacting particles is described through a time inhomogeneous transition probability kernel that depends on the ‘gradient’ of the potential field. The particles, in turn, dynamically modify the potential field through their cumulative input. Interacting Markov processes of the above form have been suggested as models for active biological transport in response to external stimulus such as a chemical gradient. One of the basic mathematical challenges is to develop a general theory of stability for such interacting Markovian systems and for the corresponding nonlinear Markov processes that arise in the large agent limit. Such a theory would be key to a mathematical understanding of the interactive structure formation that results from the complex feedback between the agents and the potential field. It will also be a crucial ingredient in developing simulation schemes that are faithful to the underlying model over long periods of time. The goal of this work is to study qualitative properties of the above stochastic system as the number of particles (N) and the time parameter (n) approach infinity. In this regard asymptotic properties of a deterministic nonlinear dynamical system, that arises in the propagation of chaos limit of the stochastic model, play a key role. We show that under suitable conditions this dynamical system has a unique fixed point. This result allows us to study stability properties of the underlying stochastic model. We show that as N → ∞, the stochastic system is well approximated by the dynamical system, uniformly over time. As a consequence, for an arbitrarily initialized system, as N → ∞ and n → ∞, the potential field and the empirical measure of the interacting particles are shown to converge to the unique fixed point of the dynamical system. In general, simulation of such interacting Markovian systems is a computationally daunting task. We propose a particle based approximation for the dynamic potential field which allows for a numerically tractable simulation scheme. It is shown that this simulation scheme well approximates the true physical system, uniformly over an infinite time horizon.



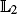 -error of the estimate of the normalising constant associated to the target. We also establish marginal propagation of chaos properties of the algorithm. These results are deduced when the cost of the algorithm is
-error of the estimate of the normalising constant associated to the target. We also establish marginal propagation of chaos properties of the algorithm. These results are deduced when the cost of the algorithm is 