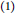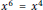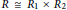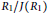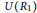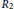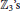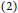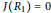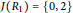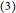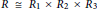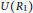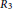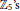Let  $R$ be a ring. The following results are proved.
$R$ be a ring. The following results are proved. 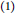 $\left( 1 \right)$ Every element of
$\left( 1 \right)$ Every element of  $R$ is a sum of an idempotent and a tripotent that commute if and only if
$R$ is a sum of an idempotent and a tripotent that commute if and only if  $R$ has the identity
$R$ has the identity 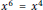 ${{x}^{6}}\,=\,{{x}^{4}}$ if and only if
${{x}^{6}}\,=\,{{x}^{4}}$ if and only if 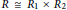 $R\,\cong \,{{R}_{1}}\,\times \,{{R}_{2}}$, where
$R\,\cong \,{{R}_{1}}\,\times \,{{R}_{2}}$, where 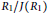 ${{{R}_{1}}}/{J\left( {{R}_{1}} \right)}\;$ is Boolean with
${{{R}_{1}}}/{J\left( {{R}_{1}} \right)}\;$ is Boolean with 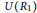 $U\left( {{R}_{1}} \right)$ a group of exponent
$U\left( {{R}_{1}} \right)$ a group of exponent  $2$ and
$2$ and 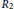 ${{R}_{2}}$ is zero or a subdirect product of
${{R}_{2}}$ is zero or a subdirect product of 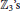 ${{\mathbb{Z}}_{3}}^{,}s$.
${{\mathbb{Z}}_{3}}^{,}s$. 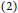 $\left( 2 \right)$ Every element of
$\left( 2 \right)$ Every element of  $R$ is either a sum or a difference of two commuting idempotents if and only if
$R$ is either a sum or a difference of two commuting idempotents if and only if 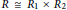 $R\,\cong \,{{R}_{1}}\,\times \,{{R}_{2}}$, where
$R\,\cong \,{{R}_{1}}\,\times \,{{R}_{2}}$, where 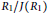 ${{{R}_{1}}}/{J\left( {{R}_{1}} \right)}\;$ is Boolean with
${{{R}_{1}}}/{J\left( {{R}_{1}} \right)}\;$ is Boolean with 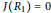 $J\left( R \right)\,=\,0$ or
$J\left( R \right)\,=\,0$ or 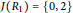 $J\left( R \right)\,=\,\left\{ 0,\,2 \right\}$ and
$J\left( R \right)\,=\,\left\{ 0,\,2 \right\}$ and 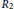 ${{R}_{2}}$ is zero or a subdirect product of
${{R}_{2}}$ is zero or a subdirect product of 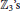 ${{\mathbb{Z}}_{3}}^{,}s$.
${{\mathbb{Z}}_{3}}^{,}s$. 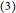 $\left( 3 \right)$ Every element of
$\left( 3 \right)$ Every element of  $R$ is a sum of two commuting tripotents if and only if
$R$ is a sum of two commuting tripotents if and only if 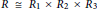 $R\,\cong \,{{R}_{1}}\,\times \,{{R}_{2}}\,\times \,{{R}_{3}}$, where
$R\,\cong \,{{R}_{1}}\,\times \,{{R}_{2}}\,\times \,{{R}_{3}}$, where 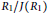 ${{{R}_{1}}}/{J\left( {{R}_{1}} \right)}\;$ is Boolean with
${{{R}_{1}}}/{J\left( {{R}_{1}} \right)}\;$ is Boolean with 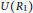 $U\left( {{R}_{1}} \right)$ a group of exponent
$U\left( {{R}_{1}} \right)$ a group of exponent  $2$
,
$2$
, 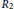 ${{R}_{2}}$ is zero or a subdirect product of
${{R}_{2}}$ is zero or a subdirect product of 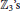 ${{\mathbb{Z}}_{3}}^{,}s$, and
${{\mathbb{Z}}_{3}}^{,}s$, and 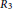 ${{R}_{3}}$ is zero or a subdirect product of
${{R}_{3}}$ is zero or a subdirect product of 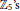 ${{\mathbb{Z}}_{5}}^{,}s$.
${{\mathbb{Z}}_{5}}^{,}s$.