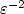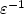Search

Skip to main content Accessibility help

Home
Search

Only show content I have access to (0)

Articles (1)

Over 3 years (1)

From year:

To year:

Apply

Mathematics (1)

periodic medium

ESAIM: Control, Optimisation and Calculus of Variations (1)

View selected items
Save to my bookmarks
Export citations
Download PDF (zip)
Save to Kindle
Save to Dropbox
Save to Google Drive
Save content to
To save content items to your account, please confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your account. Find out more about saving content to .

To save content items to your Kindle, first ensure [email protected] is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Please be advised that item(s) you selected are not available.
You are about to save
Your Kindle email address

Please provide your Kindle email.

@free.kindle.com @kindle.com (service fees apply)

By using this service, you agree that you will only keep content for personal use, and will not openly distribute them via Dropbox, Google Drive or other file sharing services

1 results

Homogenization of periodic non self-adjoint problemswith large drift and potential
Grégoire Allaire, Rafael Orive
Journal:

ESAIM: Control, Optimisation and Calculus of Variations / Volume 13 / Issue 4 / October 2007

Published online by Cambridge University Press:

20 July 2007, pp. 735-749

Print publication:

October 2007
- Article
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation
We consider the homogenization of both the parabolic and eigenvalue problems for a singularly perturbedconvection-diffusion equation in a periodic medium. All coefficients of the equation may vary both on themacroscopic scale and on the periodic microscopic scale. Denoting by ε the period, the potential or zero-orderterm is scaled as $\varepsilon^{-2}$ 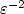and the drift or first-order term is scaled as $\varepsilon^{-1}$ 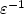. Under a structuralhypothesis on the first cell eigenvalue, which is assumed to admit a unique minimum in the domain withnon-degenerate quadratic behavior, we prove an exponential localization at this minimum point. The homogenizedproblem features a diffusion equation with quadratic potential in the whole space.