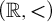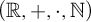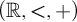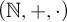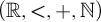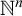We initiate an investigation of structures on the set of real numbers having the property that path components of definable sets are definable. All o-minimal structures on 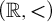 $(\mathbb {R},<)$
have the property, as do all expansions of
$(\mathbb {R},<)$
have the property, as do all expansions of 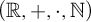 $(\mathbb {R},+,\cdot ,\mathbb {N})$
. Our main analytic-geometric result is that any such expansion of
$(\mathbb {R},+,\cdot ,\mathbb {N})$
. Our main analytic-geometric result is that any such expansion of 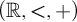 $(\mathbb {R},<,+)$
by Boolean combinations of open sets (of any arities) either is o-minimal or defines an isomorph of
$(\mathbb {R},<,+)$
by Boolean combinations of open sets (of any arities) either is o-minimal or defines an isomorph of 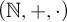 $(\mathbb N,+,\cdot )$
. We also show that any given expansion of
$(\mathbb N,+,\cdot )$
. We also show that any given expansion of 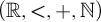 $(\mathbb {R}, <, +,\mathbb {N})$
by subsets of
$(\mathbb {R}, <, +,\mathbb {N})$
by subsets of 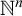 $\mathbb {N}^n$
(n allowed to vary) has the property if and only if it defines all arithmetic sets. Variations arise by considering connected components or quasicomponents instead of path components.
$\mathbb {N}^n$
(n allowed to vary) has the property if and only if it defines all arithmetic sets. Variations arise by considering connected components or quasicomponents instead of path components.