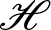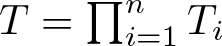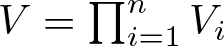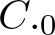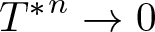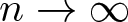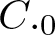For commuting contractions  $T_1,\dots,T_n$ acting on a Hilbert space
$T_1,\dots,T_n$ acting on a Hilbert space 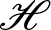 $\mathscr{H}$ with
$\mathscr{H}$ with 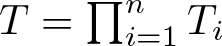 $T=\prod_{i=1}^n T_i$, we find a necessary and sufficient condition such that
$T=\prod_{i=1}^n T_i$, we find a necessary and sufficient condition such that  $(T_1,\dots,T_n)$ dilates to a commuting tuple of isometries
$(T_1,\dots,T_n)$ dilates to a commuting tuple of isometries  $(V_1,\dots,V_n)$ on the minimal isometric dilation space of T with
$(V_1,\dots,V_n)$ on the minimal isometric dilation space of T with 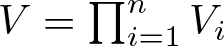 $V=\prod_{i=1}^nV_i$ being the minimal isometric dilation of T. This isometric dilation provides a commutant lifting of
$V=\prod_{i=1}^nV_i$ being the minimal isometric dilation of T. This isometric dilation provides a commutant lifting of  $(T_1, \dots, T_n)$ on the minimal isometric dilation space of T. We construct both Schäffer and Sz. Nagy–Foias-type isometric dilations for
$(T_1, \dots, T_n)$ on the minimal isometric dilation space of T. We construct both Schäffer and Sz. Nagy–Foias-type isometric dilations for  $(T_1,\dots,T_n)$ on the minimal dilation spaces of T. Also, a different dilation is constructed when the product T is a
$(T_1,\dots,T_n)$ on the minimal dilation spaces of T. Also, a different dilation is constructed when the product T is a 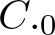 $C._0$ contraction, that is,
$C._0$ contraction, that is, 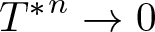 ${T^*}^n \rightarrow 0$ as
${T^*}^n \rightarrow 0$ as 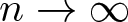 $n \rightarrow \infty$. As a consequence of these dilation theorems, we obtain different functional models for
$n \rightarrow \infty$. As a consequence of these dilation theorems, we obtain different functional models for  $(T_1,\dots,T_n)$ in terms of multiplication operators on vectorial Hardy spaces. One notable fact about our models is that the multipliers are all analytic functions in one variable. The dilation when T is a
$(T_1,\dots,T_n)$ in terms of multiplication operators on vectorial Hardy spaces. One notable fact about our models is that the multipliers are all analytic functions in one variable. The dilation when T is a 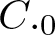 $C._0$ contraction leads to a conditional factorization of T. Several examples have been constructed.
$C._0$ contraction leads to a conditional factorization of T. Several examples have been constructed.