We study the asymptotic behaviour of the expectation of the maxima and minima of a random assignment process generated by a large matrix with multinomial entries. A variety of results is obtained for different sparsity regimes.

A new multivariate distribution possessing arbitrarily parametrized and positively dependent univariate Pareto margins is introduced. Unlike the probability law of Asimit et al. (2010), the structure in this paper is absolutely continuous with respect to the corresponding Lebesgue measure. The distribution is of importance to actuaries through its connections to the popular frailty models, as well as because of the capacity to describe dependent heavy-tailed risks. The genesis of the new distribution is linked to a number of existing probability models, and useful characteristic results are proved. Expressions for, e.g., the decumulative distribution and probability density functions, (joint) moments and regressions are developed. The distributions of minima and maxima, as well as, some weighted risk measures are employed to exemplify possible applications of the distribution in insurance.

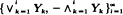We define a vector-valued scheduled maxima sequence M by considering simultaneously the maxima of several i.i.d. sequences, with the number of observations considered from each sequence at any time determined by a random scheduling sequence J. It is shown that the max-min (vector) sequence derived from i.i.d. 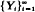can be represented as a mixture of scheduled maxima sequences, giving results for this sequence and the range 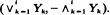A functional limit theorem for the scheduled maxima sequence shows convergence to independent extremal processes. Embedding in a scheduled extremal process gives strong laws, central limit theorems, and laws of the iterated logarithm for the record time of the scheduled maxima sequence, and hence for the max-min sequence and the range.