This paper studies the optimal allocation policy of a coherent system with independent heterogeneous components and dependent subsystems, the systems are assumed to consist of two groups of components whose lifetimes follow proportional hazard (PH) or proportional reversed hazard (PRH) models. We investigate the optimal allocation strategy by finding out the number 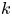$k$ of components coming from Group A in the up-series system. First, some sufficient conditions are provided in the sense of the usual stochastic order to compare the lifetimes of two-parallel–series systems with dependent subsystems, and we obtain the hazard rate and reversed hazard rate orders when two subsystems have independent lifetimes. Second, similar results are also obtained for two-series–parallel systems under certain conditions. Finally, we generalize the corresponding results to parallel–series and series–parallel systems with multiple subsystems in the viewpoint of the minimal path and the minimal cut sets, respectively. Some numerical examples are presented to illustrate the theoretical findings.

In this paper, we consider optimal components grouping in series–parallel and parallel–series systems composed of k subsystems. All components in each subsystem are drawn from a heterogeneous population consisting of m different subpopulations. Firstly, we show that when one allocation vector is majorized by another one, then the series–parallel (parallel–series) system corresponding to the first (second) vector is more reliable than that of the other. Secondly, we study the impact of changes in the number of subsystems on the system reliability. Finally, we study the influence of the selection probabilities of subpopulations on the system reliability.

In this paper, we discuss the ordering properties of sample ranges arising from multiple-outlier exponential and proportional hazard rate (PHR) models. The purpose of this paper is twofold. First, sufficient conditions on the parameter vectors are provided for the reversed hazard rate order and the usual stochastic order between the sample ranges arising from multiple-outlier exponential models with common sample size. Next, stochastic comparisons are separately carried out for sample ranges arising from multiple-outlier exponential and PHR models with different sample sizes as well as different hazard rates. Some numerical examples are also presented to illustrate the results established here.