1 results
A Short Proof of Paouris' Inequality
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 1 / 14 March 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-8
- Print publication:
- 14 March 2014
-
- Article
-
- You have access
- Export citation
-
We give a short proof of a result of G. Paouris on the tail behaviour of the Euclidean norm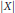
$\left| X \right|$ of an isotropic log-concave random vector 
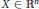$X\,\in \,{{\mathbb{R}}^{n}},$ stating that for every 
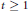$t\,\ge \,1$,
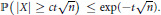$$\mathbb{P}\left( \left| X \right|\,\ge \,ct\sqrt{n} \right)\,\le \,\exp (-t\sqrt{n}).$$More precisely we show that for any log-concave random vector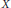
$X$ and any 
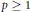$p\,\ge \,1$,
$${{(\mathbb{E}{{\left| X \right|}^{p}})}^{1/p}}\,\sim \,\mathbb{E}\left| X \right|\,+\,\underset{z\in {{S}^{n-1}}}{\mathop{\sup }}\,\,{{(\mathbb{E}{{\left| \left\langle z,\,X \right\rangle \right|}^{p}})}^{1/p}}.$$
