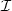In this note, we propose a general definition of shape which isboth compatible with the one proposed in phenomenology(gestaltism) and with a computer vision implementation. We reversethe usual order in Computer Vision. We do not define “shaperecognition" as a task which requires a “model" pattern which issearched in all images of a certain kind. We give instead a“blind" definition of shapes relying only on invariance and repetition arguments.Given a set of images $\cal I$ 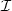 , we call shape of this set anyspatial pattern which can be found at several locations of someimage, or in several different images of $\cal I$
, we call shape of this set anyspatial pattern which can be found at several locations of someimage, or in several different images of $\cal I$ 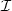 . (This meansthat the shapes of a set of images are defined without any a priori assumption or knowledge.) The definition is powerful whenit is invariant and we prove that the following invariancerequirements can be matched in theory and in practice: localcontrast invariance, robustness to blur, noise and sampling,affine deformations. We display experiments with single images and image pairs. In eachcase,we display the detected shapes. Surprisingly enough, but in accordancewith Gestalt theory,the repetition of shapes is so frequent in human environment, that manyshapes can even be learnedfrom single images.
. (This meansthat the shapes of a set of images are defined without any a priori assumption or knowledge.) The definition is powerful whenit is invariant and we prove that the following invariancerequirements can be matched in theory and in practice: localcontrast invariance, robustness to blur, noise and sampling,affine deformations. We display experiments with single images and image pairs. In eachcase,we display the detected shapes. Surprisingly enough, but in accordancewith Gestalt theory,the repetition of shapes is so frequent in human environment, that manyshapes can even be learnedfrom single images.