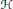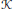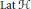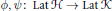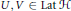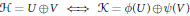1 results
Maps Preserving Complementarity of Closed Subspaces of a Hilbert Space
-
- Journal:
- Canadian Journal of Mathematics / Volume 66 / Issue 5 / 01 October 2014
- Published online by Cambridge University Press:
- 18 June 2019, pp. 1143-1166
- Print publication:
- 01 October 2014
-
- Article
-
- You have access
- Export citation
-
Let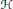
$\mathcal{H}$ and 
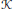$\mathcal{K}$ be infinite-dimensional separable Hilbert spaces and 
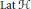$\text{Lat}\,\mathcal{H}$ the lattice of all
closed subspaces oh 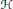$\mathcal{H}$. We describe the general form of pairs of bijective maps 
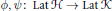$\phi ,\,\psi :\,\text{Lat}\,\mathcal{H}\,\to \,\text{Lat}\,\mathcal{K}$ having the property that for every pair 
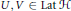$U,\,V\,\in \,\text{Lat}\,\mathcal{H}$ we have 
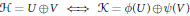$\mathcal{H}\,=\,U\,\oplus \,V\,\Leftrightarrow \,\mathcal{K}\,=\,\phi \left( U \right)\,\oplus \,\psi \,\left( V \right)$. Then we reformulate this theorem as a description of bijective image equality and kernel equality preserving maps acting on bounded linear idempotent operators. Several known structural results for maps on idempotents are easy consequences.
