We construct a Galerkin finite element method for the numerical approximation of weaksolutions to a general class of coupled FENE-type finitely extensible nonlinear elasticdumbbell models that arise from the kinetic theory of dilute solutions of polymericliquids with noninteracting polymer chains. The class of models involves the unsteadyincompressible Navier–Stokes equations in a bounded domainΩ ⊂ ℝd, d = 2 or 3, forthe velocity and the pressure of the fluid, with an elastic extra-stress tensor appearingon the right-hand side in the momentum equation. The extra-stress tensor stems from therandom movement of the polymer chains and is defined through the associated probabilitydensity function that satisfies a Fokker–Planck type parabolic equation, a crucial featureof which is the presence of a centre-of-mass diffusion term. We require no structuralassumptions on the drag term in the Fokker–Planck equation; in particular, the drag termneed not be corotational. We perform a rigorous passage to the limit as first the spatialdiscretization parameter, and then the temporal discretization parameter tend to zero, andshow that a (sub)sequence of these finite element approximations converges to a weaksolution of this coupled Navier–Stokes–Fokker–Planck system. The passage to the limit isperformed under minimal regularity assumptions on the data: a square-integrable anddivergence-free initial velocity datum \hbox{$\absundertilde$}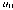${\mathit{u}}_{\mathrm{0}}{\mathrm{~}}_{}$ for the Navier–Stokes equation and a nonnegative initial probabilitydensity function ψ0 for the Fokker–Planck equation, which hasfinite relative entropy with respect to the Maxwellian M.