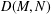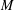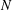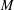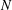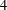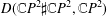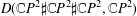This paper provides a convenient and practical method to compute the homology and intersection pairing of a branched double cover of the 4-ball.

To projections of links in the 3-ball, and to projections of surfaces in the 4-ball into the boundary sphere, we associate a sequence of homology groups, called the disoriented homology. We show that the disoriented homology is isomorphic to the homology of the double branched cover of the link or surface. We define a pairing on the first disoriented homology group of a surface and show that this is equal to the intersection pairing of the branched cover. These results generalize work of Gordon and Litherland, for embedded surfaces in the 3-sphere, to arbitrary surfaces in the 4-ball. We also give a generalization of the signature formula of Gordon–Litherland to the general setting.

Our results are underpinned by a theorem describing a handle decomposition of the branched double cover of a codimension-2 submanifold in the n-ball, which generalizes previous results of Akbulut–Kirby and others.

We study the set $D(M,N)$ of all possible mapping degrees from $M$ to $N$ when $M$ and $N$ are quasitoric $4$-manifolds. In some of the cases, we completely describe this set. Our results rely on Theorems proved by Duan and Wang and the sets of integers obtained are interesting from the number theoretical point of view, for example those representable as the sum of two squares $D(\mathbb{C}P^{2}\sharp \mathbb{C}P^{2},\mathbb{C}P^{2})$ or the sum of three squares $D(\mathbb{C}P^{2}\sharp \mathbb{C}P^{2}\sharp \mathbb{C}P^{2},\mathbb{C}P^{2})$. In addition to the general results about the mapping degrees between quasitoric 4-manifolds, we establish connections between Duan and Wang’s approach, quadratic forms, number theory and lattices.