Search

This paper deals with feedback stabilization of second order equations ofthe form

ytt + A0y + u (t) B0y (t) = 0, t ∈ [0, +∞[,

where A0 is a densely defined positive selfadjoint linear operator on areal Hilbert space H, with compact inverse and B0 is a linear map in diagonal form. It isproved here that the classical sufficient ad-condition of Jurdjevic-Quinn andBall-Slemrod with the feedback control u = ⟨yt, B0y⟩Himplies thestrong stabilization. This result is derived from a general compactnesstheorem for semigroup with compact resolvent and solves several open problems.

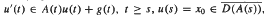In this paper we discuss the asymptotic behaviour, as t → ∞, of the integral solution u(t) of the non-linear evolution equation where {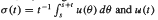A(t)}t≥0 is a family of m-dissipative operators in a Hilbert space H, and g ∈ Lloc (0, ∞ H).We give some sufficient conditions and some sufficient and necessary conditions to ensure that are weakly convergent.

Search Results

Refine search

Refine search

Actions for selected content:

2 results

Strong stabilization of controlled vibrating systems

Asymptotic behaviour of non-autonomous dissipative systems in Hilbert space

Search Results

Refine search

Refine search

Actions for selected content:

Save Search

2 results

Strong stabilization of controlled vibrating systems

Asymptotic behaviour of non-autonomous dissipative systems in Hilbert space