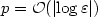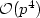We study the approximation of harmonic functions by means of harmonic polynomials intwo-dimensional, bounded, star-shaped domains. Assuming that the functions possessanalytic extensions to a δ-neighbourhood of the domain, we proveexponential convergence of the approximation error with respect to the degree of theapproximating harmonic polynomial. All the constants appearing in the bounds are explicitand depend only on the shape-regularity of the domain and on δ. We applythe obtained estimates to show exponential convergence with rate O(exp(-b√N)), N being the number of degrees offreedom and b > 0, of a hp-dGFEM discretisation ofthe Laplace equation based on piecewise harmonic polynomials. This result is animprovement over the classical rate O(exp(-b 3√N)), and is due to the use of harmonic polynomialspaces, as opposed to complete polynomial spaces.

In this work, we analyze hierarchic hp-finite element discretizations of the full, three-dimensional plate problem. Based on two-scale asymptotic expansion of the three-dimensional solution, we give specific mesh design principles for the hp-FEM which allow to resolve the three-dimensional boundary layer profiles at robust, exponential rate.We prove that, as the plate half-thickness ε tends to zero, the hp-discretization is consistent with the three-dimensional solution to any power of ε in the energy norm for the degree $p={\cal O}(\left|{\log \varepsilon}\right|)$ and with ${\cal O}({p^4})$ degrees of freedom.