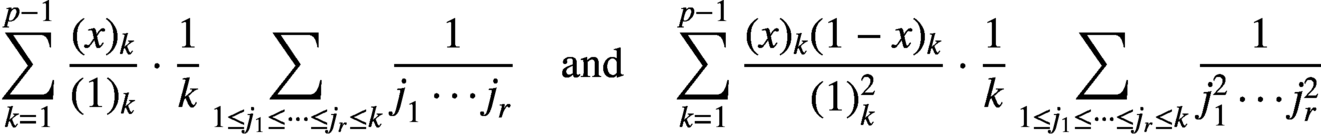1 results
TWO SUPERCONGRUENCES RELATED TO MULTIPLE HARMONIC SUMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 28 January 2021, pp. 379-389
- Print publication:
- June 2021
-
- Article
- Export citation
-
Let p be a prime and let x be a p-adic integer. We prove two supercongruences for truncated series of the form
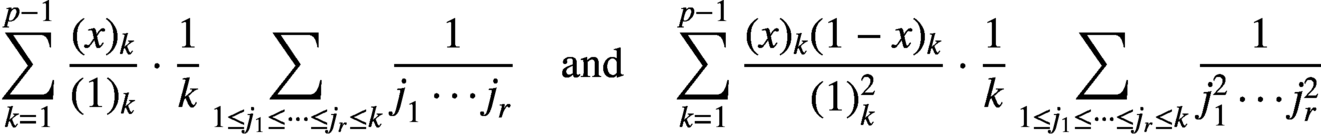
$$\begin{align*}\sum_{k=1}^{p-1} \frac{(x)_k}{(1)_k}\cdot \frac{1}{k}\sum_{1\le j_1\le\cdots\le j_r\le k}\frac{1}{j_1^{}\cdots j_r^{}}\quad\mbox{and}\quad \sum_{k=1}^{p-1} \frac{(x)_k(1-x)_k}{(1)_k^2}\cdot \frac{1}{k}\sum_{1\le j_1\le\cdots\le j_r\le k}\frac{1}{j_1^{2}\cdots j_r^{2}}\end{align*}$$which generalise previous results. We also establish q-analogues of two binomial identities.
