This paper presents a ductile damage-gradient based nonlocal and fully coupledelastoplastic constitutive equations by adding a Helmholtz equation to regularize theinitial and boundary value problem (IBVP) exhibiting some damage induced softening. First,a thermodynamically-consistent formulation of gradient-regularized plasticity fullycoupled with isotropic ductile damage and accounting for mixed non linear isotropic andkinematic hardening is presented. For the sake of simplicity, only a simplified version ofthis model based on von Mises isotropic yield function and accounting for the singlenonlinear isotropic hardening is studied and implemented numerically using an in house FEcode. An additional partial differential equation governing the evolution of the nonlocalisotropic damage is added to the equilibrium equations and the associated weak formsderived to define the IBVP (initial and boundary value problem). After the time and spacediscretization, two algebraic equations: one highly nonlinear associated with theequilibrium equation and the second purely linear associated with the damage non localityequation are obtained. Over a typical load increment, the first equation is solvediteratively thanks to the Newton-Raphson scheme and the second equation is solved directlyto compute the nonlocal damage \hbox{\Bar{{D}}}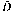 D̅ at each node. All the constitutive equations are “strongly” affected bythis nonlocal damage variable transferred to each integration point. Some applicationsshow the ability of the proposed approach to obtain a mesh independent solution for afixed value of the length scale parameter. Comparisons between fully local and nonlocalsolutions are given.
D̅ at each node. All the constitutive equations are “strongly” affected bythis nonlocal damage variable transferred to each integration point. Some applicationsshow the ability of the proposed approach to obtain a mesh independent solution for afixed value of the length scale parameter. Comparisons between fully local and nonlocalsolutions are given.