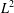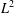This paper is concerned with the modified Wigner (respectively, Wigner–Fokker–Planck) Poisson equation. The quantum mechanical model describes the transport of charged particles under the influence of the modified Poisson potential field without (respectively, with) the collision operator. Existence and uniqueness of a global mild solution to the initial boundary value problem in one dimension are established on a weighted 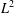 $L^{2}$ -space. The main difficulties are to derive a priori estimates on the modified Poisson equation and prove the Lipschitz properties of the appropriate potential term.
$L^{2}$ -space. The main difficulties are to derive a priori estimates on the modified Poisson equation and prove the Lipschitz properties of the appropriate potential term.
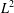 $L^{2}$ -SPACE
$L^{2}$ -SPACE