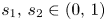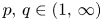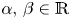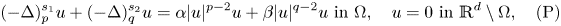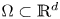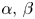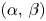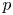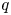2 results
On generalized eigenvalue problems of fractional (p, q)-Laplace operator with two parameters
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 January 2024, pp. 1-46
-
- Article
-
- You have access
- HTML
- Export citation
-
For $s_1,\,s_2\in (0,\,1)$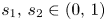
and $p,\,q \in (1,\, \infty )$
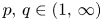, we study the following nonlinear Dirichlet eigenvalue problem with parameters $\alpha,\, \beta \in \mathbb {R}$
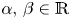driven by the sum of two nonlocal operators:\[ (-\Delta)^{s_1}_p u+(-\Delta)^{s_2}_q u=\alpha|u|^{p-2}u+\beta|u|^{q-2}u\ \text{in }\Omega, \quad u=0\ \text{in } \mathbb{R}^d \setminus \Omega, \quad \mathrm{(P)} \]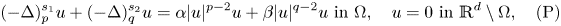where $\Omega \subset \mathbb {R}^d$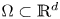
is a bounded open set. Depending on the values of $\alpha,\,\beta$
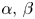, we completely describe the existence and non-existence of positive solutions to (P). We construct a continuous threshold curve in the two-dimensional $(\alpha,\, \beta )$
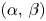-plane, which separates the regions of the existence and non-existence of positive solutions. In addition, we prove that the first Dirichlet eigenfunctions of the fractional $p$
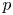-Laplace and fractional $q$
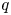-Laplace operators are linearly independent, which plays an essential role in the formation of the curve. Furthermore, we establish that every nonnegative solution of (P) is globally bounded.
RIGHT SEMIDEFINITE EIGENVALUE PROBLEMS
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 46 / Issue 3 / October 2003
- Published online by Cambridge University Press:
- 10 December 2003, pp. 561-573
-
- Article
-
- You have access
- Export citation
