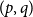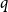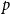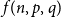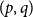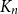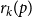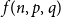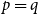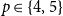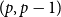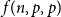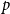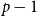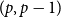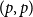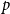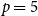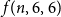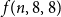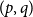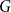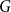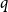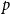A $(p,q)$ -colouring of a graph $G$ is an edge-colouring of $G$ which assigns at least $q$ colours to each $p$ -clique. The problem of determining the minimum number of colours, 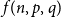$f(n,p,q)$ , needed to give a 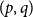$(p,q)$ -colouring of the complete graph 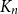$K_n$ is a natural generalization of the well-known problem of identifying the diagonal Ramsey numbers 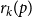$r_k(p)$ . The best-known general upper bound on 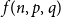$f(n,p,q)$ was given by Erdős and Gyárfás in 1997 using a probabilistic argument. Since then, improved bounds in the cases where 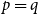$p=q$ have been obtained only for 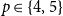$p\in \{4,5\}$ , each of which was proved by giving a deterministic construction which combined a 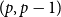$(p,p-1)$ -colouring using few colours with an algebraic colouring.

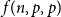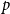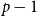In this paper, we provide a framework for proving new upper bounds on $f(n,p,p)$ in the style of these earlier constructions. We characterize all colourings of $p$ -cliques with $p-1$ colours which can appear in our modified version of the 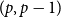$(p,p-1)$ -colouring of Conlon, Fox, Lee, and Sudakov. This allows us to greatly reduce the amount of case-checking required in identifying 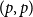$(p,p)$ -colourings, which would otherwise make this problem intractable for large values of 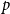$p$ . 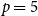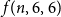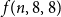In addition, we generalize our algebraic colouring from the $p=5$ setting and use this to give improved upper bounds on $f(n,6,6)$ and $f(n,8,8)$ .