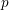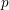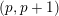In the context of propositional logics, we apply semantics modulo satisfiability—a restricted semantics which comprehends only valuations that satisfy some specific set of formulas—with the aim to efficiently solve some computational tasks. Three possible such applications are developed.

We begin by studying the possibility of implicitly representing rational McNaughton functions in Łukasiewicz Infinitely-valued Logic through semantics modulo satisfiability. We theoretically investigate some approaches to such representation concept, called representation modulo satisfiability, and describe a polynomial algorithm that builds representations in the newly introduced system. An implementation of the algorithm, test results and ways to randomly generate rational McNaughton functions for testing are presented. Moreover, we propose an application of such representations to the formal verification of properties of neural networks by means of the reasoning framework of Łukasiewicz Infinitely-valued Logic.

Then, we move to the investigation of the satisfiability of joint probabilistic assignments to formulas of Łukasiewicz Infinitely-valued Logic, which is known to be an NP-complete problem. We provide an exact decision algorithm derived from the combination of linear algebraic methods with semantics modulo satisfiability. Also, we provide an implementation for such algorithm for which the phenomenon of phase transition is empirically detected.

Lastly, we study the game theory situation of observable games, which are games that are known to reach a Nash equilibrium, however, an external observer does not know what is the exact profile of actions that occur in a specific instance; thus, such observer assigns subjective probabilities to players actions. We study the decision problem of determining if a set of these probabilistic constraints is coherent by reducing it to the problems of satisfiability of probabilistic assignments to logical formulas both in Classical Propositional Logic and Łukasiewicz Infinitely-valued Logic depending on whether only pure equilibria or also mixed equilibria are allowed. Such reductions rely upon the properties of semantics modulo satisfiability. We provide complexity and algorithmic discussion for the coherence problem and, also, for the problem of computing maximal and minimal probabilistic constraints on actions that preserves coherence.

Abstract prepared by Sandro Márcio da Silva Preto.

E-mail: [email protected]

URL:https://doi.org/10.11606/T.45.2021.tde-17062021-163257

A control system verification framework is presented for unmanned aerial vehicles using theorem proving. The framework’s aim is to set out a procedure for proving that the mathematically designed control system of the aircraft satisfies robustness requirements to ensure safe performance under varying environmental conditions. Extensive mathematical derivations, which have formerly been carried out manually, are checked for their correctness on a computer. To illustrate the procedures, a higher-order logic interactive theorem-prover and an automated theorem-prover are utilised to formally verify a nonlinear attitude control system of a generic multi-rotor UAV over a stability domain within the dynamical state space of the drone. Further benefits of the procedures are that some of the resulting methods can be implemented onboard the aircraft to detect when its controller breaches its flight envelope limits due to severe weather conditions or actuator/sensor malfunction. Such a detection procedure can be used to advise the remote pilot, or an onboard intelligent agent, to decide on some alterations of the planned flight path or to perform emergency landing.

This article analyzes the efficacy of border enforcement against smuggling. We argue that walls, fences, patrols, and other efforts to secure porous borders can reduce smuggling, but only in the absence of collusion between smugglers and state agents at official border crossings. When such corruption occurs, border enforcement merely diverts smuggling flows without reducing their overall volume. We also identify the conditions under which corruption occurs and characterize border enforcement as a sorting mechanism that allows high-skilled smugglers to forge alternative border-crossing routes while deterring low-skilled smugglers or driving them to bribe local border agents. Combining a formal model and an archival case study of opium smuggling in Southeast Asia, we demonstrate that border enforcement has conditional effects on the routes and volumes of smuggling, depending on the nature of interactions between smugglers and border agents. By drawing attention to the technological and organizational aspects of smuggling, this article brings scholarship on criminal governance into the study of international relations, and contributes to debates on the effects of border enforcement and border politics more generally.

This work extends a rule-based specification of nominal C-unification formalised in Coq to include ‘protected variables’ that cannot be instantiated during the unification process. By introducing protected variables, we are able to reuse the C-unification simplification rules to solve nominal C-matching (as well as equality check) problems. From the algorithmic point of view, this extension is sufficient to obtain a generalised C-unification procedure; however, it cannot be formally checked by simple reuse of the original formalisation. This paper describes the additional effort necessary in order to adapt the specification of the inference rules and reuse previous formalisations. We also generalise a functional recursive nominal C-unification algorithm specified in PVS with protected variables, effectively adapting this algorithm to the tasks of nominal C-matching and nominal equality check. The PVS formalisation is applied to test the correctness of a Python manual implementation of the algorithm.

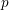By use of a natural extension map and a power series method, we obtain a local stability theorem for $p$-Kähler structures with the $(p,p+1)$th mild $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$-lemma under small differentiable deformations.

We argue that turning a logic program into a set of completed definitions can be sometimes thought of as the “reverse engineering” process of generating a set of conditions that could serve as a specification for it. Accordingly, it may be useful to define completion for a large class of Answer Set Programming (ASP) programs and to automate the process of generating and simplifying completion formulas. Examining the output produced by this kind of software may help programmers to see more clearly what their program does, and to what degree its behavior conforms with their expectations. As a step toward this goal, we propose here a definition of program completion for a large class of programs in the input language of the ASP grounder gringo, and study its properties.

Establishing the absence of deadlocks is important in many applications of formal methods. The use of model checking for finding deadlocks in formal models is often limited. In this paper, we propose a constraint-based approach to finding deadlocks employing the ProB constraint solver. We present the general technique, as well as various improvements that had to be performed on ProB's Prolog kernel, such as reification of membership and arithmetic constraints. This work was guided by an industrial case study, where a team from Bosch was modelling a cruise control system. Within this case study, ProB was able to quickly find counterexamples to very large deadlock-freedom constraints. In the paper, we also present other successful applications of this new technique. Experiments using SAT and SMT solvers on these constraints were thus far unsuccessful.

In the last decade, formal methods have proved their interest whenanalyzing security protocols. Security protocols require inparticular to reason about the attacker knowledge. Two standardnotions are often considered in formal approaches: deducibility andindistinguishability relations. The first notion states whether anattacker can learn the value of a secret, while the latter stateswhether an attacker can notice some difference between protocol runswith different values of the secret. Several decision procedureshave been developed so far for both notions but none of them can beapplied in the context of e-voting protocols, which requirededicated cryptographic primitives. In this work, we show that bothdeduction and indistinguishability are decidable in polynomial timefor two theories modeling the primitives of e-voting protocols.

Thread algebra is a semantics for recent object-oriented programming languages [J.A. Bergstra and M.E. Loots, J. Logic Algebr. Program.51 (2002) 125–156; J.A. Bergstra and C.A. Middelburg, Formal Aspects Comput. (2007)] such as C# and Java. This paper shows that thread algebra provides a process-algebraic framework for reasoning about and classifying various standard notions of noninterference, an important property in secure information flow. We will take the noninterference property given by Volpano et al. [D. Volpano, G. Smith and C. Irvine, J. Comput. Secur.4 (1996) 167–187] on type systems as an example of our approach. We define a comparable notion of noninterference in the setting of thread algebra. Our approach gives a similar result to the approach of [G. Smith and D. Volpano, in POPL'9829 (1998) 355–364] and can be applied to unstructured and multithreaded programming languages.