1 results
Multiple solutions for a critical fractional elliptic system involving concave–convex nonlinearities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 6 / December 2016
- Published online by Cambridge University Press:
- 27 October 2016, pp. 1167-1193
- Print publication:
- December 2016
-
- Article
- Export citation
-
We are concerned with the multiplicity of solutions to the system driven by a fractional operator with homogeneous Dirichlet boundary conditions. Namely, using fibering maps and the Nehari manifold, we obtain multiple solutions to the following fractional elliptic system:
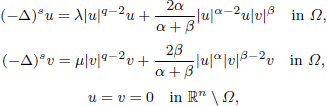
where Ω is a smooth bounded set in ℝn , n > 2s, with s ∈ (0, 1); (–Δ)s is the fractional Laplace operator;, λ, μ > 0 are two parameters; the exponent n/(n – 2s) ⩽ q < 2; α > 1, β > 1 satisfy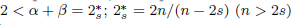
is the fractional critical Sobolev exponent.
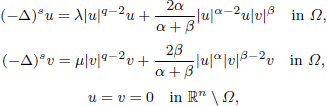
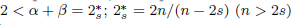is the fractional critical Sobolev exponent.