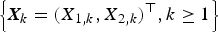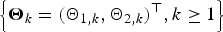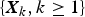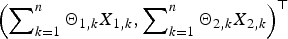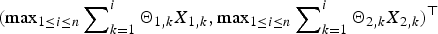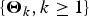Let 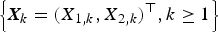$\left\{ {{\bi X}_k = {(X_{1,k},X_{2,k})}^{\top}, k \ge 1} \right\}$ be a sequence of independent and identically distributed random vectors whose components are allowed to be generally dependent with marginal distributions being from the class of extended regular variation, and let 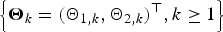$\left\{ {{\brTheta} _k = {(\Theta _{1,k},\Theta _{2,k})}^{\top}, k \ge 1} \right\}$ be a sequence of nonnegative random vectors that is independent of 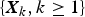$\left\{ {{\bi X}_k, k \ge 1} \right\}$. Under several mild assumptions, some simple asymptotic formulae of the tail probabilities for the bidimensional randomly weighted sums 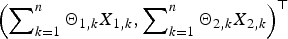$\left( {\sum\nolimits_{k = 1}^n {\Theta _{1,k}} X_{1,k},\sum\nolimits_{k = 1}^n {\Theta _{2,k}} X_{2,k}} \right)^{\rm \top }$ and their maxima 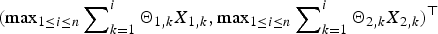$({{\max} _{1 \le i \le n}}\sum\nolimits_{k = 1}^i {\Theta _{1,k}} X_{1,k},{{\max} _{1 \le i \le n}}\sum\nolimits_{k = 1}^i {\Theta _{2,k}} X_{2,k})^{\rm \top }$ are established. Moreover, uniformity of the estimate can be achieved under some technical moment conditions on 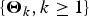$\left\{ {{\brTheta} _k, k \ge 1} \right\}$. Direct applications of the results to risk analysis are proposed, with two types of ruin probability for a discrete-time bidimensional risk model being evaluated.

Consider a continuous-time renewal risk model with a constant force of interest. We assume that claim sizes and interarrival times correspondingly form a sequence of independent and identically distributed random pairs and that each pair obeys a dependence structure described via the conditional tail probability of a claim size given the interarrival time before the claim. We focus on determining the impact of this dependence structure on the asymptotic tail probability of discounted aggregate claims. Assuming that the claim size distribution is subexponential, we derive an exact locally uniform asymptotic formula, which quantitatively captures the impact of the dependence structure. When the claim size distribution is extended regularly varying tailed, we show that this asymptotic formula is globally uniform.

We study the tail behavior of discounted aggregate claims in a continuous-time renewal model. For the case of Pareto-type claims, we establish a tail asymptotic formula, which holds uniformly in time.

This paper investigates the finite- and infinite-time ruin probabilities in a discrete-time stochastic economic environment. Under the assumption that the insurance risk - the total net loss within one time period - is extended-regularly-varying or rapidly-varying tailed, various precise estimates for the ruin probabilities are derived. In particular, some estimates obtained are uniform with respect to the time horizon, and so apply in the case of infinite-time ruin.