1 results
Décomposition de Hodge pour l’homologie stable des groupes d’automorphismes des groupes libres
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 9 / September 2019
- Published online by Cambridge University Press:
- 07 August 2019, pp. 1794-1844
- Print publication:
- September 2019
-
- Article
-
- You have access
- HTML
- Export citation
-
On établit une décomposition de l’homologie stable des groupes d’automorphismes des groupes libres à coefficients polynomiaux contravariants en termes d’homologie des foncteurs. Elle permet plusieurs calculs explicites, qui recoupent des résultats établis de manière indépendante par O. Randal-Williams et généralisent certains d’entre eux. Nos méthodes reposent sur l’examen d’extensions de Kan dérivées associées à plusieurs catégories de groupes libres, la généralisation d’un critère d’annulation homologique à coefficients polynomiaux dû à Scorichenko, le théorème de Galatius identifiant l’homologie stable des groupes d’automorphismes des groupes libres à celle des groupes symétriques, la machinerie des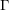
$\unicode[STIX]{x1D6E4}$-espaces et le scindement de Snaith.
