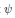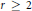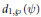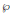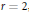Let 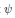 $\psi$ be a generic Drinfeld module of rank
$\psi$ be a generic Drinfeld module of rank 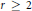 $r\,\ge \,2$ . We study the first elementary divisor
$r\,\ge \,2$ . We study the first elementary divisor 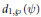 ${{d}_{1,\,\wp }}\,\left( \psi\right)$ of the reduction of
${{d}_{1,\,\wp }}\,\left( \psi\right)$ of the reduction of 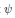 $\psi$ modulo a prime
$\psi$ modulo a prime 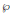 $\wp $ , as
$\wp $ , as 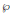 $\wp $ varies. In particular, we prove the existence of the density of the primes
$\wp $ varies. In particular, we prove the existence of the density of the primes 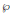 $\wp $ for which
$\wp $ for which 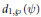 ${{d}_{1,\,\wp }}\,\left( \psi\right)$ is fixed. For
${{d}_{1,\,\wp }}\,\left( \psi\right)$ is fixed. For 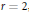 $r\,=\,2$ , we also study the second elementary divisor (the exponent) of the reduction of
$r\,=\,2$ , we also study the second elementary divisor (the exponent) of the reduction of 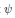 $\psi$ modulo
$\psi$ modulo 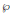 $\wp $ and prove that, on average, it has a large norm. Our work is motivated by J.-P. Serre's study of an elliptic curve analogue of Artin's Primitive Root Conjecture, and, moreover, by refinements to Serre's study developed by the first author and M. R. Murty.
$\wp $ and prove that, on average, it has a large norm. Our work is motivated by J.-P. Serre's study of an elliptic curve analogue of Artin's Primitive Root Conjecture, and, moreover, by refinements to Serre's study developed by the first author and M. R. Murty.