We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We prove an equivalence between weighted Poincaré inequalities and the existence of weak solutions to a Neumann problem related to a degenerate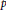 
$p$-Laplacian. The Poincaré inequalities are formulated in the context of degenerate Sobolev spaces defined in terms of a quadratic form, and the associated matrix is the source of the degeneracy in the 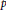$p$-Laplacian.
