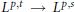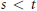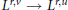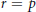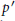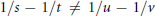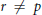We study when the spaces of Lorentz multipliers from 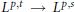 ${{L}^{p,t\,}}\to \,{{L}^{p,s}}$ are distinct. Our main interest is the case when
${{L}^{p,t\,}}\to \,{{L}^{p,s}}$ are distinct. Our main interest is the case when 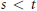 $s\,<\,t$, the Lorentz-improving multipliers. We prove, for example, that the space of multipliers which map
$s\,<\,t$, the Lorentz-improving multipliers. We prove, for example, that the space of multipliers which map 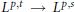 ${{L}^{p,t\,}}\to \,{{L}^{p,s}}$ is different from those mapping
${{L}^{p,t\,}}\to \,{{L}^{p,s}}$ is different from those mapping 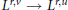 ${{L}^{r,v}}\,\to \,{{L}^{r,u}}$ if either
${{L}^{r,v}}\,\to \,{{L}^{r,u}}$ if either 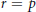 $r\,=\,p$ or
$r\,=\,p$ or 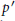 ${p}'$ and
${p}'$ and 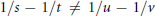 $1/s\,-\,1/t\,\ne \,1/u\,-\,1/v$, or
$1/s\,-\,1/t\,\ne \,1/u\,-\,1/v$, or 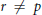 $r\,\ne \,p$ or
$r\,\ne \,p$ or 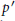 ${p}'$. These results are obtained by making careful estimates of the Lorentz multiplier norms of certain linear combinations of Fejer or Dirichlet kernels. For the case when the first indices are different the linear combination we analyze is in the spirit of a Rudin-Shapiro polynomial.
${p}'$. These results are obtained by making careful estimates of the Lorentz multiplier norms of certain linear combinations of Fejer or Dirichlet kernels. For the case when the first indices are different the linear combination we analyze is in the spirit of a Rudin-Shapiro polynomial.

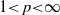 , let
, let 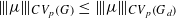 , for
, for 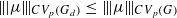 . These inequalities were already known for
. These inequalities were already known for 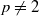 . Finally, for
. Finally, for