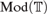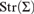A notion of strictly primitive recursive realizability is introduced by Damnjanovic in 1994. It is a kind of constructive semantics of the arithmetical sentences using primitive recursive functions. It is of interest to study the corresponding predicate logic. It was argued by Park in 2003 that the predicate logic of strictly primitive recursive realizability is not arithmetical. Park’s argument is essentially based on a claim of Damnjanovic that intuitionistic logic is sound with respect to strictly primitive recursive realizability, but that claim was disproved by the author of this article in 2006. The aim of this paper is to present a correct proof of the result of Park.

Classically, any structure for a signature ${\rm{\Sigma }}$ may be completed to a model of a desired regular theory ${T}}$ by means of the chase construction or small object argument. Moreover, this exhibits 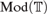${\rm{Mod}}\left(T)$ as weakly reflective in 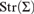${\rm{Str}}\left( {\rm{\Sigma }} \right)$.

We investigate this in the constructive setting. The basic construction is unproblematic; however, it is no longer a weak reflection. Indeed, we show that various reflectivity principles for models of regular theories are equivalent to choice principles in the ambient set theory. However, the embedding of a structure into its chase-completion still satisfies a conservativity property, which suffices for applications such as the completeness of regular logic with respect to Tarski (i.e., set) models.

Unlike most constructive developments of predicate logic, we do not assume that equality between symbols in the signature is decidable. While in this setting, we also give a version of one classical lemma which is trivial over discrete signatures but more interesting here: the abstraction of constants in a proof to variables.