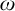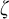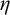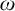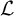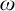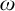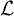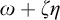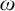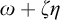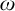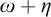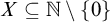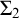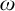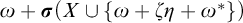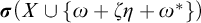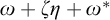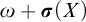Cohesive powers of computable structures are effective analogs of ultrapowers, where cohesive sets play the role of ultrafilters. Let 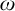$\omega $, 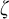$\zeta $, and 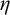$\eta $ denote the respective order-types of the natural numbers, the integers, and the rationals when thought of as linear orders. We investigate the cohesive powers of computable linear orders, with special emphasis on computable copies of 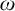$\omega $. If 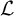$\mathcal {L}$ is a computable copy of 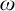$\omega $ that is computably isomorphic to the usual presentation of 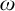$\omega $, then every cohesive power of 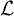$\mathcal {L}$ has order-type 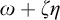$\omega + \zeta \eta $. However, there are computable copies of 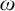$\omega $, necessarily not computably isomorphic to the usual presentation, having cohesive powers not elementarily equivalent to 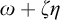$\omega + \zeta \eta $. For example, we show that there is a computable copy of 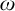$\omega $ with a cohesive power of order-type 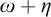$\omega + \eta $. Our most general result is that if 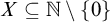$X \subseteq \mathbb {N} \setminus \{0\}$ is a Boolean combination of 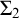$\Sigma _2$ sets, thought of as a set of finite order-types, then there is a computable copy of 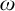$\omega $ with a cohesive power of order-type 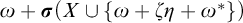$\omega + \boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$, where 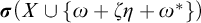$\boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$ denotes the shuffle of the order-types in X and the order-type 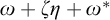$\omega + \zeta \eta + \omega ^*$. Furthermore, if X is finite and non-empty, then there is a computable copy of 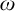$\omega $ with a cohesive power of order-type 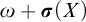$\omega + \boldsymbol {\sigma }(X)$.

We describe punctual categoricity in several natural classes, including binary relational structures and mono-unary functional structures. We prove that every punctually categorical structure in a finite unary language is ${\text {PA}}(0')$-categorical, and we show that this upper bound is tight. We also construct an example of a punctually categorical structure whose degree of categoricity is $0''$. We also prove that, with a bit of work, the latter result can be pushed beyond $\Delta ^1_1$, thus showing that punctually categorical structures can possess arbitrarily complex automorphism orbits.

As a consequence, it follows that binary relational structures and unary structures are not universal with respect to primitive recursive interpretations; equivalently, in these classes every rich enough interpretation technique must necessarily involve unbounded existential quantification or infinite disjunction. In contrast, it is well-known that both classes are universal for Turing computability.