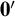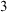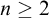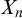A Polish space is not always homeomorphic to a computably presented Polish space. In this article, we examine degrees of non-computability of presenting homeomorphic copies of compact Polish spaces. We show that there exists a $\mathbf {0}'$-computable low$_3$ compact Polish space which is not homeomorphic to a computable one, and that, for any natural number $n\geq 2$, there exists a Polish space $X_n$ such that exactly the high$_{n}$-degrees are required to present the homeomorphism type of $X_n$. Along the way we investigate the computable aspects of Čech homology groups. We also show that no compact Polish space has a least presentation with respect to Turing reducibility.

Computable analysis provides ways of representing points in a topological space, and therefore of defining a notion of computable points of the space. In this article, we investigate when two topologies on the same space induce different sets of computable points. We first study a purely topological version of the problem, which is to understand when two topologies are not 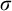$\sigma $-homeomorphic. We obtain a characterization leading to an effective version, and we prove that two topologies satisfying this condition induce different sets of computable points. Along the way, we propose an effective version of the Baire category theorem which captures the construction technique, and enables one to build points satisfying properties that are co-meager with respect to a topology, and are computable with respect to another topology. Finally, we generalize the result to three topologies and give an application to prove that certain sets do not have computable type, which means that they have a homeomorphic copy that is semicomputable but not computable.