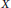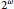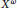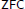1 results
Countable Dense Homogeneity in Powers of Zero-dimensional Definable Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 2 / 01 June 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 334-349
- Print publication:
- 01 June 2015
-
- Article
-
- You have access
- Export citation
-
We show that for a coanalytic subspace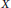
$X$ of 
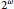${{2}^{\omega }}$, the countable dense homogeneity of 
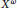${{X}^{\omega }}$ is equivalent to 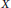$X$ being Polish. This strengthens a result of Hrušák and Zamora Avilés. Then, inspired by results of Hernández-Gutiérrez, Hrušák, and van Mill, using a technique of Medvedev, we construct a non-Polish subspace 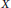$X$ of 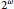${{2}^{\omega }}$ such that 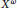${{X}^{\omega }}$ is countable dense homogeneous. This gives the first 
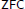$\text{ZFC}$ answer to a question of Hrušák and Zamora Avilés. Furthermore, since our example is consistently analytic, the equivalence result mentioned above is sharp. Our results also answer a question of Medini and Milovich. Finally, we show that if every countable subset of a zero-dimensional separable metrizable space 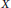$X$ is included in a Polish subspace of 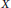$X$, then 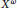${{X}^{\omega }}$ is countable dense homogeneous.
