We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We provide an alternative view of some results in [1, 3, 11]. In particular, we prove that (1) if a continuous self-map of a compact metric space has the shadowing, then the union of the basins of terminal chain components is a dense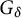 
$G_\delta $-subset of the space; and (2) if a continuous self-map of a locally connected compact metric space has the shadowing, and if the chain recurrent set is totally disconnected, then the map is almost chain continuous.
Let M be a closed n-dimensional smooth Riemannian manifold, and let X be a 
$C^1$-vector field of 
$M.$ Let 
$\gamma $ be a hyperbolic closed orbit of 
$X.$ In this paper, we show that X has the 
$C^1$-stably shadowing property on the chain component 
$C_X(\gamma )$ if and only if 
$C_X(\gamma )$ is the hyperbolic homoclinic class.
