1 results
A NEW APPROACH TO SELECT THE BEST SUBSET OF PREDICTORS IN LINEAR REGRESSION MODELLING: BI-OBJECTIVE MIXED INTEGER LINEAR PROGRAMMING
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 11 January 2019, pp. 64-75
-
- Article
-
- You have access
- Export citation
-
We study the problem of choosing the best subset of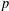
$p$ features in linear regression, given 
$n$ observations. This problem naturally contains two objective functions including minimizing the amount of bias and minimizing the number of predictors. The existing approaches transform the problem into a single-objective optimization problem. We explain the main weaknesses of existing approaches and, to overcome their drawbacks, we propose a bi-objective mixed integer linear programming approach. A computational study shows the efficacy of the proposed approach.
