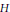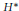We develop the transversal harmonic theory for a transversally symplectic flow on a manifold and establish the transversal hard Lefschetz theorem. Our main results extend the cases for a contact manifold (H. Kitahara and H. K. Pak, ‘A note on harmonic forms on a compact manifold’, Kyungpook Math. J.43 (2003), 1–10) and for an almost cosymplectic manifold (R. Ibanez, ‘Harmonic cohomology classes of almost cosymplectic manifolds’, Michigan Math. J.44 (1997), 183–199). For the point foliation these are the results obtained by Brylinski (‘A differential complex for Poisson manifold’, J. Differential Geom.28 (1988), 93–114), Haller (‘Harmonic cohomology of symplectic manifolds’, Adv. Math.180 (2003), 87–103), Mathieu (‘Harmonic cohomology classes of symplectic manifolds’, Comment. Math. Helv.70 (1995), 1–9) and Yan (‘Hodge structure on symplectic manifolds’, Adv. Math.120 (1996), 143–154).

Recently [8], a harmonic theory was developed for a compact contact manifold from the viewpoint of the transversal geometry of contact flow. A contact flow is a typical example of geodesible flow. As a natural generalization of the contact flow, the present paper develops a harmonic theory for various flows on compact manifolds. We introduce the notions of $H$-harmonic and ${{H}^{*}}$-harmonic spaces associated to a Hörmander flow. We also introduce the notions of basic harmonic spaces associated to a weak basic flow. One of our main results is to show that in the special case of isometric flow these harmonic spaces are isomorphic to the cohomology spaces of certain complexes. Moreover, we find an obstruction for a geodesible flow to be isometric.

In this paper, we consider the relationship between the cohomologies of the basic differential forms and the transverse holonomy groupoid of a foliation. Applications to minimal models are given.