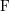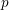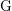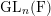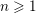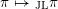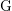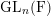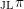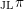We show how the modular representation theory of inner forms of general linear groups over a non-Archimedean local field can be brought to bear on the complex theory in a remarkable way. Let $\text{F}$ be a non-Archimedean locally compact field of residue characteristic $p$, and let $\text{G}$ be an inner form of the general linear group $\text{GL}_{n}(\text{F})$ for $n\geqslant 1$. We consider the problem of describing explicitly the local Jacquet–Langlands correspondence $\unicode[STIX]{x1D70B}\mapsto _{\text{JL}}\unicode[STIX]{x1D70B}$ between the complex discrete series representations of $\text{G}$ and $\text{GL}_{n}(\text{F})$, in terms of type theory. We show that the congruence properties of the local Jacquet–Langlands correspondence exhibited by A. Mínguez and the first author give information about the explicit description of this correspondence. We prove that the problem of the invariance of the endo-class by the Jacquet–Langlands correspondence can be reduced to the case where the representations $\unicode[STIX]{x1D70B}$ and $_{\text{JL}}\unicode[STIX]{x1D70B}$ are both cuspidal with torsion number $1$. We also give an explicit description of the Jacquet–Langlands correspondence for all essentially tame discrete series representations of $\text{G}$, up to an unramified twist, in terms of admissible pairs, generalizing previous results by Bushnell and Henniart. In positive depth, our results are the first beyond the case where $\unicode[STIX]{x1D70B}$ and $_{\text{JL}}\unicode[STIX]{x1D70B}$ are both cuspidal.

Let F be a non-Archimedean local field. Let $\mathcal{G}_n^{\rm et}(F)$ be the set of equivalence classes of irreducible, n-dimensional representations of the Weil group $\mathcal{W}_F$ of F which are essentially tame. Let $\mathcal{A}_n^{\rm et}(F)$ be the set of equivalence classes of irreducible, essentially tame, supercuspidal representations of GLn(F). The Langlands correspondence induces a canonical bijection $\mathcal{L}:\mathcal{G}_n^{\rm et}(F) \to \mathcal{A}_n^{\rm et}(F)$. We continue the programme of describing this map in terms of explicit descriptions of the sets $\mathcal{G}_n^{\rm et}(F)$ and $\mathcal{A}_n^{\rm et}(F)$. These descriptions are in terms of admissible pairs $(E/F, \xi)$, consisting of a tamely ramified field extension $E/F$ of degree n and a quasicharacter $\xi$ of $E^\times$ subject to certain technical conditions. If Pn(F) is the set of isomorphism classes of admissible pairs of degree n, we have explicit bijections $P_n(F) \cong \mathcal{G}_n^{\rm et}(F)$ and $P_n(F) \cong \mathcal{A}_n^{\rm et}(F)$. In an earlier paper we showed that, if $\sigma \in \mathcal{G}_n^{\rm et}(F)$ corresponds to an admissible pair $(E/F,\xi)$, then $\mathcal{L}(\sigma)$ corresponds to the admissible pair $(E/F,\mu\xi)$, for a certain tamely ramified character $\mu$ of $E^\times$. In this paper, we determine the character $\mu$ when $E/F$ is totally ramified.