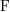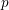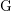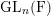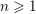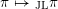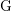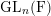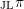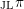1 Introduction
1.1 Background
Let
![]() $\text{F}$
be a non-Archimedean locally compact field of residue characteristic
$\text{F}$
be a non-Archimedean locally compact field of residue characteristic
![]() $p$
, let
$p$
, let
![]() $\text{H}$
be the general linear group
$\text{H}$
be the general linear group
![]() $\text{GL}_{n}(\text{F})$
for
$\text{GL}_{n}(\text{F})$
for
![]() $n\geqslant 1$
, and let
$n\geqslant 1$
, and let
![]() $\text{G}$
be an inner form of
$\text{G}$
be an inner form of
![]() $\text{H}$
. This is a group of the form
$\text{H}$
. This is a group of the form
![]() $\text{GL}_{m}(\text{D})$
, where
$\text{GL}_{m}(\text{D})$
, where
![]() $m$
divides
$m$
divides
![]() $n$
and
$n$
and
![]() $\text{D}$
is a central division
$\text{D}$
is a central division
![]() $\text{F}$
-algebra whose reduced degree is denoted by
$\text{F}$
-algebra whose reduced degree is denoted by
![]() $d$
, with
$d$
, with
![]() $n=md$
. Let
$n=md$
. Let
![]() $\mathscr{D}(\text{G},\mathbf{C})$
denote the set of all isomorphism classes of essentially square-integrable, irreducible complex smooth representations of
$\mathscr{D}(\text{G},\mathbf{C})$
denote the set of all isomorphism classes of essentially square-integrable, irreducible complex smooth representations of
![]() $\text{G}$
. The local Jacquet–Langlands correspondence [Reference Jacquet and LanglandsJL70, Reference RogawskiRog83, Reference Deligne, Kazhdan and VignérasDKV84, Reference BadulescuBad02] is a bijection
$\text{G}$
. The local Jacquet–Langlands correspondence [Reference Jacquet and LanglandsJL70, Reference RogawskiRog83, Reference Deligne, Kazhdan and VignérasDKV84, Reference BadulescuBad02] is a bijection
specified by a character relation on elliptic regular conjugacy classes. Bushnell and Henniart have elaborated a vast programme that aims to give an explicit description of this correspondence [Reference HenniartHen93, Reference Bushnell and HenniartBH00, Reference Bushnell and HenniartBH05a, Reference Bushnell and HenniartBH11a]. The present article is a contribution to this programme.
We first have to explain what we mean by an explicit description of the Jacquet–Langlands correspondence. Essentially square-integrable representations of
![]() $\text{G}$
can be described in terms of parabolic induction. Given such a representation
$\text{G}$
can be described in terms of parabolic induction. Given such a representation
![]() $\unicode[STIX]{x1D70B}$
, there exist a unique integer
$\unicode[STIX]{x1D70B}$
, there exist a unique integer
![]() $r$
dividing
$r$
dividing
![]() $m$
and a cuspidal irreducible representation
$m$
and a cuspidal irreducible representation
![]() $\unicode[STIX]{x1D70C}$
of
$\unicode[STIX]{x1D70C}$
of
![]() $\text{GL}_{m/r}(\text{D})$
, unique up to isomorphism, such that
$\text{GL}_{m/r}(\text{D})$
, unique up to isomorphism, such that
![]() $\unicode[STIX]{x1D70B}$
is isomorphic to the unique irreducible quotient of the parabolically induced representation
$\unicode[STIX]{x1D70B}$
is isomorphic to the unique irreducible quotient of the parabolically induced representation
where
![]() $\unicode[STIX]{x1D708}$
is the unramified character ‘absolute value of the reduced norm’ and
$\unicode[STIX]{x1D708}$
is the unramified character ‘absolute value of the reduced norm’ and
![]() $s(\unicode[STIX]{x1D70C})$
is a positive integer dividing
$s(\unicode[STIX]{x1D70C})$
is a positive integer dividing
![]() $d$
, associated to
$d$
, associated to
![]() $\unicode[STIX]{x1D70C}$
in [Reference TadićTad90]. The essentially square-integrable representation
$\unicode[STIX]{x1D70C}$
in [Reference TadićTad90]. The essentially square-integrable representation
![]() $\unicode[STIX]{x1D70B}$
is entirely characterized by the pair
$\unicode[STIX]{x1D70B}$
is entirely characterized by the pair
![]() $(\unicode[STIX]{x1D70C},r)$
; this goes back to Bernstein and Zelevinski [Reference ZelevinskiZel80] in the case where
$(\unicode[STIX]{x1D70C},r)$
; this goes back to Bernstein and Zelevinski [Reference ZelevinskiZel80] in the case where
![]() $\text{D}$
is equal to
$\text{D}$
is equal to
![]() $\text{F}$
, and to Tadić [Reference TadićTad90] in the general case (see also Badulescu [Reference BadulescuBad07] for the case where
$\text{F}$
, and to Tadić [Reference TadićTad90] in the general case (see also Badulescu [Reference BadulescuBad07] for the case where
![]() $\text{F}$
has positive characteristic). In particular, we may write
$\text{F}$
has positive characteristic). In particular, we may write
![]() $s(\unicode[STIX]{x1D70B})=s(\unicode[STIX]{x1D70C})$
. Similarly, associated with the Jacquet-Langlands transfer
$s(\unicode[STIX]{x1D70B})=s(\unicode[STIX]{x1D70C})$
. Similarly, associated with the Jacquet-Langlands transfer
![]() $_{\text{JL}}\unicode[STIX]{x1D70B}$
are an integer
$_{\text{JL}}\unicode[STIX]{x1D70B}$
are an integer
![]() $u$
dividing
$u$
dividing
![]() $n$
and a cuspidal irreducible representation
$n$
and a cuspidal irreducible representation
![]() $\unicode[STIX]{x1D70E}$
of
$\unicode[STIX]{x1D70E}$
of
![]() $\text{GL}_{n/u}(\text{F})$
. The integers
$\text{GL}_{n/u}(\text{F})$
. The integers
![]() $r$
and
$r$
and
![]() $u$
are related by the identity
$u$
are related by the identity
![]() $u=rs(\unicode[STIX]{x1D70B})$
. It remains to understand how the cuspidal representations
$u=rs(\unicode[STIX]{x1D70B})$
. It remains to understand how the cuspidal representations
![]() $\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D70C}$
and
![]() $\unicode[STIX]{x1D70E}$
are related.
$\unicode[STIX]{x1D70E}$
are related.
Thanks to the theory of simple types, developed by Bushnell and Kutzko [Reference Bushnell and KutzkoBK93] for the general linear group
![]() $\text{GL}_{n}(\text{F})$
and by Broussous [Reference BroussousBro98] and the authors [Reference SécherreSéc04, Reference SécherreSéc05a, Reference SécherreSéc05b, Reference Sécherre and StevensSS08] for its inner forms, the cuspidal representation
$\text{GL}_{n}(\text{F})$
and by Broussous [Reference BroussousBro98] and the authors [Reference SécherreSéc04, Reference SécherreSéc05a, Reference SécherreSéc05b, Reference Sécherre and StevensSS08] for its inner forms, the cuspidal representation
![]() $\unicode[STIX]{x1D70C}$
is compactly induced from a compact-mod-centre, open subgroup. More precisely, there is an extended maximal simple type, composed of a compact-mod-centre subgroup
$\unicode[STIX]{x1D70C}$
is compactly induced from a compact-mod-centre, open subgroup. More precisely, there is an extended maximal simple type, composed of a compact-mod-centre subgroup
![]() $\mathbf{\text{J}}$
of
$\mathbf{\text{J}}$
of
![]() $\text{GL}_{m/r}(\text{D})$
and an irreducible representation
$\text{GL}_{m/r}(\text{D})$
and an irreducible representation
![]() $\boldsymbol{\unicode[STIX]{x1D706}}$
of
$\boldsymbol{\unicode[STIX]{x1D706}}$
of
![]() $\mathbf{\text{J}}$
, both constructed in a very specific way, such that the compact induction of
$\mathbf{\text{J}}$
, both constructed in a very specific way, such that the compact induction of
![]() $\boldsymbol{\unicode[STIX]{x1D706}}$
to
$\boldsymbol{\unicode[STIX]{x1D706}}$
to
![]() $\text{GL}_{m/r}(\text{D})$
is irreducible and isomorphic to
$\text{GL}_{m/r}(\text{D})$
is irreducible and isomorphic to
![]() $\unicode[STIX]{x1D70C}$
. Such a type is uniquely determined up to conjugacy. Giving an explicit description of the local Jacquet–Langlands correspondence will thus consist of describing the extended maximal simple type associated with the representation
$\unicode[STIX]{x1D70C}$
. Such a type is uniquely determined up to conjugacy. Giving an explicit description of the local Jacquet–Langlands correspondence will thus consist of describing the extended maximal simple type associated with the representation
![]() $\unicode[STIX]{x1D70E}$
in terms of that of
$\unicode[STIX]{x1D70E}$
in terms of that of
![]() $\unicode[STIX]{x1D70C}$
.
$\unicode[STIX]{x1D70C}$
.
This programme was first carried out for essentially square-integrable representations of depth zero by Silberger and Zink [Reference Silberger and ZinkSZ03, Reference Silberger and ZinkSZ05] and by Bushnell and Henniart [Reference Bushnell and HenniartBH11b]. Before explaining the other cases which have already been dealt with, we need to introduce two numerical invariants associated to an essentially square-integrable, irreducible representation of
![]() $\text{G}$
. Such a representation
$\text{G}$
. Such a representation
![]() $\unicode[STIX]{x1D70B}$
has: a torsion number
$\unicode[STIX]{x1D70B}$
has: a torsion number
![]() $t(\unicode[STIX]{x1D70B})$
, the number of unramified characters
$t(\unicode[STIX]{x1D70B})$
, the number of unramified characters
![]() $\unicode[STIX]{x1D712}$
of
$\unicode[STIX]{x1D712}$
of
![]() $\text{G}$
such that the twisted representation
$\text{G}$
such that the twisted representation
![]() $\unicode[STIX]{x1D70B}\unicode[STIX]{x1D712}$
is isomorphic to
$\unicode[STIX]{x1D70B}\unicode[STIX]{x1D712}$
is isomorphic to
![]() $\unicode[STIX]{x1D70B}$
; and a parametric degree
$\unicode[STIX]{x1D70B}$
; and a parametric degree
![]() $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70B})$
, defined in [Reference Bushnell and HenniartBH11a] via the theory of simple types, which is a multiple of
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70B})$
, defined in [Reference Bushnell and HenniartBH11a] via the theory of simple types, which is a multiple of
![]() $t(\unicode[STIX]{x1D70B})$
and divides
$t(\unicode[STIX]{x1D70B})$
and divides
![]() $n$
. Both of these integers are invariant under the Jacquet–Langlands correspondence [Reference Bushnell and HenniartBH11a]. It is interesting to note that the invariance of the parametric degree implies that
$n$
. Both of these integers are invariant under the Jacquet–Langlands correspondence [Reference Bushnell and HenniartBH11a]. It is interesting to note that the invariance of the parametric degree implies that
![]() $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70B})s(\unicode[STIX]{x1D70B})=n/r$
. Consequently, the representation
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70B})s(\unicode[STIX]{x1D70B})=n/r$
. Consequently, the representation
![]() $_{\text{JL}}\unicode[STIX]{x1D70B}$
is cuspidal if and only if the parametric degree of
$_{\text{JL}}\unicode[STIX]{x1D70B}$
is cuspidal if and only if the parametric degree of
![]() $\unicode[STIX]{x1D70B}$
is equal to
$\unicode[STIX]{x1D70B}$
is equal to
![]() $n$
.
$n$
.
In [Reference Bushnell and HenniartBH11a], Bushnell and Henniart treat the case where the cuspidal representation
![]() $\unicode[STIX]{x1D70B}$
is essentially tame (that is,
$\unicode[STIX]{x1D70B}$
is essentially tame (that is,
![]() $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70B})/t(\unicode[STIX]{x1D70B})$
is prime to
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70B})/t(\unicode[STIX]{x1D70B})$
is prime to
![]() $p$
) and of parametric degree
$p$
) and of parametric degree
![]() $n$
. In that case, they explicitly describe the Jacquet–Langlands correspondence by parametrizing the conjugacy classes of extended maximal simple types in
$n$
. In that case, they explicitly describe the Jacquet–Langlands correspondence by parametrizing the conjugacy classes of extended maximal simple types in
![]() $\text{G}$
and
$\text{G}$
and
![]() $\text{H}$
by objects called admissible pairs [Reference HoweHow77]. (We will see these objects in § 9.)
$\text{H}$
by objects called admissible pairs [Reference HoweHow77]. (We will see these objects in § 9.)
In [Reference Bushnell and HenniartBH05a], Bushnell and Henniart also treat the case which is in some sense at the opposite extreme to the essentially tame case, where
![]() $n$
is of the form
$n$
is of the form
![]() $p^{k}$
, with
$p^{k}$
, with
![]() $k\geqslant 1$
and
$k\geqslant 1$
and
![]() $p\neq 2$
, and
$p\neq 2$
, and
![]() $\unicode[STIX]{x1D70B}$
is a cuspidal representation of
$\unicode[STIX]{x1D70B}$
is a cuspidal representation of
![]() $\text{D}^{\times }$
which is maximal totally ramified (that is,
$\text{D}^{\times }$
which is maximal totally ramified (that is,
![]() $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70B})=n$
and
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70B})=n$
and
![]() $t(\unicode[STIX]{x1D70B})=1$
).
$t(\unicode[STIX]{x1D70B})=1$
).
In [Reference Imai and TsushimaIT18], Imai and Tsushima treat the case where
![]() $\unicode[STIX]{x1D70B}$
is an epipelagic cuspidal representation of
$\unicode[STIX]{x1D70B}$
is an epipelagic cuspidal representation of
![]() $\text{G}$
, that is, of depth
$\text{G}$
, that is, of depth
![]() $1/n$
. Such representations are maximal totally ramified.
$1/n$
. Such representations are maximal totally ramified.
With the exception of [Reference Silberger and ZinkSZ03, Reference Silberger and ZinkSZ05] and [Reference Bushnell and HenniartBH11b], these results all concern cases where the representations
![]() $\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}$
and
![]() $_{\text{JL}}\unicode[STIX]{x1D70B}$
are both cuspidal, that is, where
$_{\text{JL}}\unicode[STIX]{x1D70B}$
are both cuspidal, that is, where
![]() $\unicode[STIX]{x1D70B}$
is of parametric degree
$\unicode[STIX]{x1D70B}$
is of parametric degree
![]() $n$
. In such cases, since the cuspidal representation
$n$
. In such cases, since the cuspidal representation
![]() $\unicode[STIX]{x1D70B}$
can be expressed as the compact induction of an extended maximal simple type
$\unicode[STIX]{x1D70B}$
can be expressed as the compact induction of an extended maximal simple type
![]() $(\mathbf{\text{J}},\boldsymbol{\unicode[STIX]{x1D706}})$
, there is a relatively straightforward formula giving the trace of
$(\mathbf{\text{J}},\boldsymbol{\unicode[STIX]{x1D706}})$
, there is a relatively straightforward formula giving the trace of
![]() $\unicode[STIX]{x1D70B}$
at an elliptic regular element in terms of the trace of
$\unicode[STIX]{x1D70B}$
at an elliptic regular element in terms of the trace of
![]() $\boldsymbol{\unicode[STIX]{x1D706}}$
(see [Reference Bushnell and HenniartBH96, Theorem A.14] and [Reference Bushnell and HenniartBH11a, (1.2.2)]). The strategies followed in [Reference Bushnell and HenniartBH11a, Reference Bushnell and HenniartBH05a] and [Reference Imai and TsushimaIT18] depend crucially on such a formula. When considering a non-cuspidal essentially square-integrable representation, we are in a much less favourable situation. For the group
$\boldsymbol{\unicode[STIX]{x1D706}}$
(see [Reference Bushnell and HenniartBH96, Theorem A.14] and [Reference Bushnell and HenniartBH11a, (1.2.2)]). The strategies followed in [Reference Bushnell and HenniartBH11a, Reference Bushnell and HenniartBH05a] and [Reference Imai and TsushimaIT18] depend crucially on such a formula. When considering a non-cuspidal essentially square-integrable representation, we are in a much less favourable situation. For the group
![]() $\text{GL}_{n}(\text{F})$
, Broussous [Reference BroussousBro14] and Broussous together with Schneider [Reference Broussous and SchneiderBS17] have obtained formulae expressing the trace of such a representation at an elliptic regular element by bringing in the theory of simple types. However, in this article, we follow a different route.
$\text{GL}_{n}(\text{F})$
, Broussous [Reference BroussousBro14] and Broussous together with Schneider [Reference Broussous and SchneiderBS17] have obtained formulae expressing the trace of such a representation at an elliptic regular element by bringing in the theory of simple types. However, in this article, we follow a different route.
1.2 Preservation of endo-classes
An important first step towards the general case is to look at the behaviour of the local Jacquet–Langlands correspondence with respect to endo-classes. An endo-class (over
![]() $\text{F}$
) is a type-theoretic invariant associated to any essentially square-integrable representation of any inner form of any general linear group over
$\text{F}$
) is a type-theoretic invariant associated to any essentially square-integrable representation of any inner form of any general linear group over
![]() $\text{F}$
, whose construction requires considerable machinery [Reference Bushnell and HenniartBH96, Reference Broussous, Sécherre and StevensBSS12]. However, for cuspidal representations of
$\text{F}$
, whose construction requires considerable machinery [Reference Bushnell and HenniartBH96, Reference Broussous, Sécherre and StevensBSS12]. However, for cuspidal representations of
![]() $\text{H}$
, it turns out to have a rather simple arithmetical interpretation through the local Langlands correspondence [Reference Bushnell and HenniartBH03]. Indeed, two cuspidal irreducible representations of general linear groups over
$\text{H}$
, it turns out to have a rather simple arithmetical interpretation through the local Langlands correspondence [Reference Bushnell and HenniartBH03]. Indeed, two cuspidal irreducible representations of general linear groups over
![]() $\text{F}$
have the same endo-class if and only if the irreducible representations of the absolute Weil group
$\text{F}$
have the same endo-class if and only if the irreducible representations of the absolute Weil group
![]() $\mathscr{W}_{\text{F}}$
associated to them by the local Langlands correspondence share an irreducible component when restricted to the wild inertia subgroup
$\mathscr{W}_{\text{F}}$
associated to them by the local Langlands correspondence share an irreducible component when restricted to the wild inertia subgroup
![]() $\mathscr{P}_{\text{F}}$
. The local Langlands correspondence thus induces a bijection between the set of
$\mathscr{P}_{\text{F}}$
. The local Langlands correspondence thus induces a bijection between the set of
![]() $\mathscr{W}_{\text{F}}$
-conjugacy classes of irreducible representations of
$\mathscr{W}_{\text{F}}$
-conjugacy classes of irreducible representations of
![]() $\mathscr{P}_{\text{F}}$
and the set
$\mathscr{P}_{\text{F}}$
and the set
![]() $\mathscr{E}(\text{F})$
of endo-classes over
$\mathscr{E}(\text{F})$
of endo-classes over
![]() $\text{F}$
.
$\text{F}$
.
It is expected that the local Jacquet–Langlands correspondence preserves endo-classes. More precisely, there is the following conjecture.
Endo-class Invariance Conjecture. For any essentially square-integrable, irreducible complex representation
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $\text{G}$
, the endo-classes of
$\text{G}$
, the endo-classes of
![]() $\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}$
and
![]() $_{\text{JL}}\unicode[STIX]{x1D70B}$
are the same.
$_{\text{JL}}\unicode[STIX]{x1D70B}$
are the same.
Our first main result is the following (see Theorem 7.1), which reduces this conjecture to the case of maximal totally ramified cuspidal representations.
Theorem A. Assume that, for all
![]() $\text{F}$
and
$\text{F}$
and
![]() $n$
and for all cuspidal irreducible complex representations
$n$
and for all cuspidal irreducible complex representations
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $\text{G}$
such that
$\text{G}$
such that
![]() $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70B})=n$
and
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70B})=n$
and
![]() $t(\unicode[STIX]{x1D70B})=1$
, the cuspidal representations
$t(\unicode[STIX]{x1D70B})=1$
, the cuspidal representations
![]() $\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}$
and
![]() $_{\text{JL}}\unicode[STIX]{x1D70B}$
have the same endo-class. Then the Endo-class Invariance Conjecture is true.
$_{\text{JL}}\unicode[STIX]{x1D70B}$
have the same endo-class. Then the Endo-class Invariance Conjecture is true.
Before explaining our strategy, we must first take a detour through the modular representation theory of
![]() $\text{G}$
and explain recent developments concerning the modular properties of the Jacquet–Langlands correspondence. Fix a prime number
$\text{G}$
and explain recent developments concerning the modular properties of the Jacquet–Langlands correspondence. Fix a prime number
![]() $\ell$
different from
$\ell$
different from
![]() $p$
, and consider the smooth
$p$
, and consider the smooth
![]() $\ell$
-adic representations of
$\ell$
-adic representations of
![]() $\text{G}$
, that is, those with coefficients in the algebraic closure
$\text{G}$
, that is, those with coefficients in the algebraic closure
![]() $\overline{\mathbf{Q}}_{\ell }$
of the field of
$\overline{\mathbf{Q}}_{\ell }$
of the field of
![]() $\ell$
-adic numbers. There is then the notion of integral irreducible representation of
$\ell$
-adic numbers. There is then the notion of integral irreducible representation of
![]() $\text{G}$
: one containing a
$\text{G}$
: one containing a
![]() $\text{G}$
-stable
$\text{G}$
-stable
![]() $\overline{\mathbf{Z}}_{\ell }$
-lattice (where
$\overline{\mathbf{Z}}_{\ell }$
-lattice (where
![]() $\overline{\mathbf{Z}}_{\ell }$
is the ring of integers of
$\overline{\mathbf{Z}}_{\ell }$
is the ring of integers of
![]() $\overline{\mathbf{Q}}_{\ell }$
), which can then be reduced modulo
$\overline{\mathbf{Q}}_{\ell }$
), which can then be reduced modulo
![]() $\ell$
. More precisely, given such a representation
$\ell$
. More precisely, given such a representation
![]() $\unicode[STIX]{x1D70B}$
containing a stable
$\unicode[STIX]{x1D70B}$
containing a stable
![]() $\overline{\mathbf{Z}}_{\ell }$
-lattice
$\overline{\mathbf{Z}}_{\ell }$
-lattice
![]() $\unicode[STIX]{x1D6EC}$
, Vignéras [Reference VignérasVig96, Reference VignérasVig04] showed that the representation
$\unicode[STIX]{x1D6EC}$
, Vignéras [Reference VignérasVig96, Reference VignérasVig04] showed that the representation
![]() $\unicode[STIX]{x1D6EC}\,\otimes \,_{\overline{\mathbf{Z}}_{\ell }}\overline{\mathbf{F}}_{\ell }$
is smooth of finite length (where
$\unicode[STIX]{x1D6EC}\,\otimes \,_{\overline{\mathbf{Z}}_{\ell }}\overline{\mathbf{F}}_{\ell }$
is smooth of finite length (where
![]() $\overline{\mathbf{F}}_{\ell }$
is the residue field of
$\overline{\mathbf{F}}_{\ell }$
is the residue field of
![]() $\overline{\mathbf{Z}}_{\ell }$
), and its semi-simplification is independent of the choice of
$\overline{\mathbf{Z}}_{\ell }$
), and its semi-simplification is independent of the choice of
![]() $\unicode[STIX]{x1D6EC}$
; we call this semi-simplification the reduction mod
$\unicode[STIX]{x1D6EC}$
; we call this semi-simplification the reduction mod
![]() $\ell$
of
$\ell$
of
![]() $\unicode[STIX]{x1D70B}$
. Thus we can say that two integral irreducible
$\unicode[STIX]{x1D70B}$
. Thus we can say that two integral irreducible
![]() $\ell$
-adic representations of
$\ell$
-adic representations of
![]() $\text{G}$
are congruent mod
$\text{G}$
are congruent mod
![]() $\ell$
if their reductions mod
$\ell$
if their reductions mod
![]() $\ell$
are isomorphic.
$\ell$
are isomorphic.
To relate this to the local Jacquet–Langlands correspondence, we fix an isomorphism of fields between
![]() $\mathbf{C}$
and
$\mathbf{C}$
and
![]() $\overline{\mathbf{Q}}_{\ell }$
; replacing one by the other via this isomorphism, we get an
$\overline{\mathbf{Q}}_{\ell }$
; replacing one by the other via this isomorphism, we get an
![]() $\ell$
-adic Jacquet–Langlands correspondence
$\ell$
-adic Jacquet–Langlands correspondence
which is independent of the choice of isomorphism. Thus one can study the compatibility of this correspondence with the relation of congruence mod
![]() $\ell$
, which was done by Dat [Reference DatDat12] and then in full generality by Mínguez and the first author [Reference Mínguez and SécherreMS17]: two integral representations of
$\ell$
, which was done by Dat [Reference DatDat12] and then in full generality by Mínguez and the first author [Reference Mínguez and SécherreMS17]: two integral representations of
![]() $\mathscr{D}(\text{G},\overline{\mathbf{Q}}_{\ell })$
are congruent mod
$\mathscr{D}(\text{G},\overline{\mathbf{Q}}_{\ell })$
are congruent mod
![]() $\ell$
if and only if their images under the
$\ell$
if and only if their images under the
![]() $\ell$
-adic Jacquet–Langlands correspondence are congruent mod
$\ell$
-adic Jacquet–Langlands correspondence are congruent mod
![]() $\ell$
(see [Reference Mínguez and SécherreMS17, Théorème 1.1]).
$\ell$
(see [Reference Mínguez and SécherreMS17, Théorème 1.1]).
We now need to explain how modular representation theory can give us information on the complex representation theory. The starting point of our strategy to prove Theorem A using modular methods is the fact that two representations of
![]() $\mathscr{D}(\text{G},\overline{\mathbf{Q}}_{\ell })$
which are congruent mod
$\mathscr{D}(\text{G},\overline{\mathbf{Q}}_{\ell })$
which are congruent mod
![]() $\ell$
have the same endo-class. The converse is of course not true, but we will see that one can nevertheless link two essentially square-integrable representations with the same endo-class by a chain of congruence relations. Let us explain this in more detail.
$\ell$
have the same endo-class. The converse is of course not true, but we will see that one can nevertheless link two essentially square-integrable representations with the same endo-class by a chain of congruence relations. Let us explain this in more detail.
Firstly, for any irreducible
![]() $\ell$
-adic representation of
$\ell$
-adic representation of
![]() $\text{G}$
, we have a notion of mod-
$\text{G}$
, we have a notion of mod-
![]() $\ell$
inertial supercuspidal support (see Definition 4.1 and also [Reference HelmHel16] in the split case), coming from the notion of supercuspidal support for irreducible representations of
$\ell$
inertial supercuspidal support (see Definition 4.1 and also [Reference HelmHel16] in the split case), coming from the notion of supercuspidal support for irreducible representations of
![]() $\text{G}$
with coefficients in
$\text{G}$
with coefficients in
![]() $\overline{\mathbf{F}}_{\ell }$
, defined in [Reference Mínguez and SécherreMS14a]. Two irreducible complex representations of
$\overline{\mathbf{F}}_{\ell }$
, defined in [Reference Mínguez and SécherreMS14a]. Two irreducible complex representations of
![]() $\text{G}$
are said to be
$\text{G}$
are said to be
![]() $\ell$
-linked (Definitions 5.1 and 4.2) if there is a field isomorphism
$\ell$
-linked (Definitions 5.1 and 4.2) if there is a field isomorphism
![]() $\mathbf{C}\simeq \overline{\mathbf{Q}}_{\ell }$
such that the resulting irreducible
$\mathbf{C}\simeq \overline{\mathbf{Q}}_{\ell }$
such that the resulting irreducible
![]() $\ell$
-adic representations have the same mod-
$\ell$
-adic representations have the same mod-
![]() $\ell$
inertial supercuspidal support. This is independent of the choice of field isomorphism, and it is not hard to show, using the work done in [Reference Mínguez and SécherreMS17], that the Jacquet–Langlands correspondence preserves the relation of being
$\ell$
inertial supercuspidal support. This is independent of the choice of field isomorphism, and it is not hard to show, using the work done in [Reference Mínguez and SécherreMS17], that the Jacquet–Langlands correspondence preserves the relation of being
![]() $\ell$
-linked for essentially square-integrable representations (Propositions 6.1 and 6.2). We can now introduce the following definition (Definition 5.6).
$\ell$
-linked for essentially square-integrable representations (Propositions 6.1 and 6.2). We can now introduce the following definition (Definition 5.6).
Definition. Two irreducible complex representations
![]() $\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}$
and
![]() $\unicode[STIX]{x1D70B}\text{sp}\prime$
of
$\unicode[STIX]{x1D70B}\text{sp}\prime$
of
![]() $\text{G}$
are said to be linked if there are a finite sequence of prime numbers
$\text{G}$
are said to be linked if there are a finite sequence of prime numbers
![]() $\ell _{1},\ldots ,\ell _{r}$
, all different from
$\ell _{1},\ldots ,\ell _{r}$
, all different from
![]() $p$
, and a finite sequence of irreducible complex representations
$p$
, and a finite sequence of irreducible complex representations
![]() $\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{0},\unicode[STIX]{x1D70B}_{1},\ldots ,\unicode[STIX]{x1D70B}_{r}=\unicode[STIX]{x1D70B}\text{sp}\prime$
such that, for each
$\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{0},\unicode[STIX]{x1D70B}_{1},\ldots ,\unicode[STIX]{x1D70B}_{r}=\unicode[STIX]{x1D70B}\text{sp}\prime$
such that, for each
![]() $i\in \{1,\ldots ,r\}$
, the representations
$i\in \{1,\ldots ,r\}$
, the representations
![]() $\unicode[STIX]{x1D70B}_{i-1}$
and
$\unicode[STIX]{x1D70B}_{i-1}$
and
![]() $\unicode[STIX]{x1D70B}_{i}$
are
$\unicode[STIX]{x1D70B}_{i}$
are
![]() $\ell _{i}$
-linked.
$\ell _{i}$
-linked.
Two essentially square-integrable complex representations which are linked have the same endo-class. More generally, if we define the semi-simple endo-class of an irreducible representation to be the weighted formal sum of the endo-classes of the cuspidal representations in its cuspidal support (with multiplicities determined by the sizes of the groups, see (5.2)), then two irreducible representations which are linked have the same semi-simple endo-class. The interest of the definition is apparent from the following theorem (see Theorem 5.10), which says that the converse is also true.
Theorem B. Two irreducible complex representations of
![]() $\text{G}$
are linked if and only if they have the same semi-simple endo-class.
$\text{G}$
are linked if and only if they have the same semi-simple endo-class.
In particular, two essentially square-integrable complex representations have the same endo-class if and only if they are linked; moreover, one can then link them by a sequence of essentially square-integrable representations (Remark 5.9).
Theorem B gives a remarkable reinterpretation of what it means for two irreducible complex representations to have the same semi-simple endo-class. Beyond the intrinsic interest in explicating the notion of endo-class and its relation with modular representation theory, the main interest in this reformulation comes from the fact that, applying results from [Reference Mínguez and SécherreMS17], we prove the following (Theorem 6.3).
Theorem C. Two essentially square-integrable complex representations of
![]() $\text{G}$
are linked if and only if their transfers to
$\text{G}$
are linked if and only if their transfers to
![]() $\text{H}$
are linked.
$\text{H}$
are linked.
It follows from Theorems B and C that two essentially square-integrable complex representations of
![]() $\text{G}$
have the same endo-class if and only if their transfers to
$\text{G}$
have the same endo-class if and only if their transfers to
![]() $\text{H}$
have the same endo-class. Thus, denoting by
$\text{H}$
have the same endo-class. Thus, denoting by
![]() $\mathscr{E}_{n}(\text{F})$
the set of endo-classes over
$\mathscr{E}_{n}(\text{F})$
the set of endo-classes over
![]() $\text{F}$
with degree dividing
$\text{F}$
with degree dividing
![]() $n$
, the Jacquet–Langlands correspondence induces a bijection
$n$
, the Jacquet–Langlands correspondence induces a bijection
We now make the following observation (Proposition 6.5).
Proposition. For every essentially square-integrable complex representation of
![]() $\text{G}$
, there is a cuspidal complex representation of
$\text{G}$
, there is a cuspidal complex representation of
![]() $\text{G}$
with the same endo-class and with parametric degree
$\text{G}$
with the same endo-class and with parametric degree
![]() $n$
.
$n$
.
To prove the conjecture (that is, to prove that
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}_{1}$
is the identity map), it is therefore sufficient to prove that, for every cuspidal complex representation
$\boldsymbol{\unicode[STIX]{x1D70B}}_{1}$
is the identity map), it is therefore sufficient to prove that, for every cuspidal complex representation
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $\text{G}$
of parametric degree
$\text{G}$
of parametric degree
![]() $n$
, the representations
$n$
, the representations
![]() $\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}$
and
![]() $_{\text{JL}}\unicode[STIX]{x1D70B}$
have the same endo-class. Using techniques developed in [Reference Bushnell and HenniartBH11a, § 6], we can go further and show that one need only consider cuspidal representations of parametric degree
$_{\text{JL}}\unicode[STIX]{x1D70B}$
have the same endo-class. Using techniques developed in [Reference Bushnell and HenniartBH11a, § 6], we can go further and show that one need only consider cuspidal representations of parametric degree
![]() $n$
and torsion number
$n$
and torsion number
![]() $1$
, thus obtaining Theorem C. Therefore, to prove the Endo-class Invariance Conjecture, it remains only to prove the following conjecture. We say that an endo-class is totally ramified if it has residual degree
$1$
, thus obtaining Theorem C. Therefore, to prove the Endo-class Invariance Conjecture, it remains only to prove the following conjecture. We say that an endo-class is totally ramified if it has residual degree
![]() $1$
, that is, if its tame parameter field (in the sense of [Reference Bushnell and HenniartBH14, § 2]) is totally ramified.
$1$
, that is, if its tame parameter field (in the sense of [Reference Bushnell and HenniartBH14, § 2]) is totally ramified.
Conjecture. For all
![]() $\text{F}$
and
$\text{F}$
and
![]() $n$
, and for every totally ramified
$n$
, and for every totally ramified
![]() $\text{F}$
-endo-class
$\text{F}$
-endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
of degree
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
of degree
![]() $n$
, there is a cuspidal complex representation
$n$
, there is a cuspidal complex representation
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $\text{G}$
with endo-class
$\text{G}$
with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
such that
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
such that
![]() $_{\text{JL}}\unicode[STIX]{x1D70B}$
has endo-class
$_{\text{JL}}\unicode[STIX]{x1D70B}$
has endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
.
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
.
This conjecture is known to be true in all the cases where the explicit correspondence is known (see § 1.1). See also the remark at the end of this introduction for more recent developments.
1.3 The level-zero part
We now leave to one side the preservation of endo-classes and move on to the next step towards an explicit description of the Jacquet–Langlands correspondence. We will see that the modular methods described in the previous paragraphs can be pushed further to yield additional information. Let
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
be an endo-class of degree dividing
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
be an endo-class of degree dividing
![]() $n$
, and suppose that it is invariant under the Jacquet–Langlands correspondence, that is,
$n$
, and suppose that it is invariant under the Jacquet–Langlands correspondence, that is,
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}_{1}(\boldsymbol{\unicode[STIX]{x1D6E9}})=\boldsymbol{\unicode[STIX]{x1D6E9}}$
. (See the remark at the end of this introduction for a discussion of this assumption.) The correspondence thus induces a bijection between isomorphism classes of essentially square-integrable complex representations of
$\boldsymbol{\unicode[STIX]{x1D70B}}_{1}(\boldsymbol{\unicode[STIX]{x1D6E9}})=\boldsymbol{\unicode[STIX]{x1D6E9}}$
. (See the remark at the end of this introduction for a discussion of this assumption.) The correspondence thus induces a bijection between isomorphism classes of essentially square-integrable complex representations of
![]() $\text{G}$
with endo-class
$\text{G}$
with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
and those of
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
and those of
![]() $\text{H}$
. Since the correspondence is also compatible with unramified twisting, we get a bijection
$\text{H}$
. Since the correspondence is also compatible with unramified twisting, we get a bijection
where
![]() $\mathscr{D}_{0}(\text{G},\boldsymbol{\unicode[STIX]{x1D6E9}})$
denotes the set of inertial classes of essentially square-integrable complex representations of
$\mathscr{D}_{0}(\text{G},\boldsymbol{\unicode[STIX]{x1D6E9}})$
denotes the set of inertial classes of essentially square-integrable complex representations of
![]() $\text{G}$
with endo-class
$\text{G}$
with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
. The theory of simple types [Reference Bushnell and KutzkoBK93, Reference SécherreSéc05b, Reference Sécherre and StevensSS08, Reference Sécherre and StevensSS12] gives us a canonical bijection between
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
. The theory of simple types [Reference Bushnell and KutzkoBK93, Reference SécherreSéc05b, Reference Sécherre and StevensSS08, Reference Sécherre and StevensSS12] gives us a canonical bijection between
![]() $\mathscr{D}_{0}(\text{G},\boldsymbol{\unicode[STIX]{x1D6E9}})$
and the set
$\mathscr{D}_{0}(\text{G},\boldsymbol{\unicode[STIX]{x1D6E9}})$
and the set
![]() $\mathscr{T}(\text{G},\boldsymbol{\unicode[STIX]{x1D6E9}})$
of
$\mathscr{T}(\text{G},\boldsymbol{\unicode[STIX]{x1D6E9}})$
of
![]() $\text{G}$
-conjugacy classes of simple types, for
$\text{G}$
-conjugacy classes of simple types, for
![]() $\text{G}$
with endo-class
$\text{G}$
with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
. More precisely, the inertial class of an essentially square-integrable complex representation
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
. More precisely, the inertial class of an essentially square-integrable complex representation
![]() $\unicode[STIX]{x1D70B}$
corresponds to the conjugacy class of a simple type
$\unicode[STIX]{x1D70B}$
corresponds to the conjugacy class of a simple type
![]() $(\text{J},\unicode[STIX]{x1D706})$
, formed of a compact open subgroup
$(\text{J},\unicode[STIX]{x1D706})$
, formed of a compact open subgroup
![]() $\text{J}$
of
$\text{J}$
of
![]() $\text{G}$
and an irreducible representation
$\text{G}$
and an irreducible representation
![]() $\unicode[STIX]{x1D706}$
of
$\unicode[STIX]{x1D706}$
of
![]() $\text{J}$
, if and only if
$\text{J}$
, if and only if
![]() $\unicode[STIX]{x1D706}$
is an irreducible component of the restriction of
$\unicode[STIX]{x1D706}$
is an irreducible component of the restriction of
![]() $\unicode[STIX]{x1D70B}$
to
$\unicode[STIX]{x1D70B}$
to
![]() $\text{J}$
. Thus we get a bijection
$\text{J}$
. Thus we get a bijection
To go further, we need to enter into the detail of the structure of simple types (see § 3.3).
Given a simple type
![]() $(\text{J},\unicode[STIX]{x1D706})$
of
$(\text{J},\unicode[STIX]{x1D706})$
of
![]() $\text{G}$
with endo-class
$\text{G}$
with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
, the group
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
, the group
![]() $\text{J}$
contains a unique maximal normal pro-
$\text{J}$
contains a unique maximal normal pro-
![]() $p$
subgroup, denoted by
$p$
subgroup, denoted by
![]() $\text{J}^{1}$
. The restriction of
$\text{J}^{1}$
. The restriction of
![]() $\unicode[STIX]{x1D706}$
to
$\unicode[STIX]{x1D706}$
to
![]() $\text{J}^{1}$
is isotypic, that is, it is a direct sum of copies of a single irreducible representation
$\text{J}^{1}$
is isotypic, that is, it is a direct sum of copies of a single irreducible representation
![]() $\unicode[STIX]{x1D702}$
. This representation
$\unicode[STIX]{x1D702}$
. This representation
![]() $\unicode[STIX]{x1D702}$
can be extended to a representation of
$\unicode[STIX]{x1D702}$
can be extended to a representation of
![]() $\text{J}$
with the same intertwining set as
$\text{J}$
with the same intertwining set as
![]() $\unicode[STIX]{x1D702}$
. If we fix such an extension
$\unicode[STIX]{x1D702}$
. If we fix such an extension
![]() $\unicode[STIX]{x1D705}$
, then the representation
$\unicode[STIX]{x1D705}$
, then the representation
![]() $\unicode[STIX]{x1D706}$
can be expressed in the form
$\unicode[STIX]{x1D706}$
can be expressed in the form
![]() $\unicode[STIX]{x1D705}\,\otimes \,\unicode[STIX]{x1D70E}$
, where
$\unicode[STIX]{x1D705}\,\otimes \,\unicode[STIX]{x1D70E}$
, where
![]() $\unicode[STIX]{x1D70E}$
is an irreducible representation of
$\unicode[STIX]{x1D70E}$
is an irreducible representation of
![]() $\text{J}$
that is trivial on
$\text{J}$
that is trivial on
![]() $\text{J}^{1}$
.
$\text{J}^{1}$
.
The quotient group
![]() $\text{J}/\text{J}^{1}$
is (non-canonically) isomorphic to a product of copies of a single general linear group over a finite field
$\text{J}/\text{J}^{1}$
is (non-canonically) isomorphic to a product of copies of a single general linear group over a finite field
![]() $\boldsymbol{d}$
, and
$\boldsymbol{d}$
, and
![]() $\unicode[STIX]{x1D70E}$
, viewed as a representation of such a product, is the tensor product of copies of a single cuspidal representation. A theorem of Green [Reference GreenGre96] allows us to parametrize
$\unicode[STIX]{x1D70E}$
, viewed as a representation of such a product, is the tensor product of copies of a single cuspidal representation. A theorem of Green [Reference GreenGre96] allows us to parametrize
![]() $\unicode[STIX]{x1D70E}$
by a character of
$\unicode[STIX]{x1D70E}$
by a character of
![]() $\boldsymbol{k}^{\times }$
, where
$\boldsymbol{k}^{\times }$
, where
![]() $\boldsymbol{k}$
is a suitable extension of
$\boldsymbol{k}$
is a suitable extension of
![]() $\boldsymbol{d}$
. This character is determined up to conjugation by the Galois group of
$\boldsymbol{d}$
. This character is determined up to conjugation by the Galois group of
![]() $\boldsymbol{k}$
over a certain subfield
$\boldsymbol{k}$
over a certain subfield
![]() $\boldsymbol{e}$
of
$\boldsymbol{e}$
of
![]() $\boldsymbol{d}$
.
$\boldsymbol{d}$
.
We denote by
![]() $\text{X}$
the group of characters of
$\text{X}$
the group of characters of
![]() $\boldsymbol{k}^{\times }$
and by
$\boldsymbol{k}^{\times }$
and by
![]() $\unicode[STIX]{x1D6E4}$
the Galois group
$\unicode[STIX]{x1D6E4}$
the Galois group
![]() $\text{Gal}(\boldsymbol{k}/\boldsymbol{e})$
. Fixing once and for all a choice of representation
$\text{Gal}(\boldsymbol{k}/\boldsymbol{e})$
. Fixing once and for all a choice of representation
![]() $\unicode[STIX]{x1D705}$
for a maximal simple type in
$\unicode[STIX]{x1D705}$
for a maximal simple type in
![]() $\text{G}$
with endo-class
$\text{G}$
with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
, we get a bijection from
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
, we get a bijection from
![]() $\text{X}/\unicode[STIX]{x1D6E4}$
to
$\text{X}/\unicode[STIX]{x1D6E4}$
to
![]() $\mathscr{T}(\text{G},\boldsymbol{\unicode[STIX]{x1D6E9}})$
(see § 3.3 for details). Making a similar choice for
$\mathscr{T}(\text{G},\boldsymbol{\unicode[STIX]{x1D6E9}})$
(see § 3.3 for details). Making a similar choice for
![]() $\text{H}$
, we also get a bijection from
$\text{H}$
, we also get a bijection from
![]() $\text{X}/\unicode[STIX]{x1D6E4}$
to
$\text{X}/\unicode[STIX]{x1D6E4}$
to
![]() $\mathscr{T}(\text{H},\boldsymbol{\unicode[STIX]{x1D6E9}})$
. Composing this with (1.1) gives a permutation
$\mathscr{T}(\text{H},\boldsymbol{\unicode[STIX]{x1D6E9}})$
. Composing this with (1.1) gives a permutation
which depends on various choices (see § 8.1). Although one could fix choices, it is not clear which are the natural ones in general, so we must take care with them. In particular, we will see that in the essentially tame case, one can make sense of the notion of a compatible choice for
![]() $\text{G}$
and
$\text{G}$
and
![]() $\text{H}$
.
$\text{H}$
.
We write
![]() $[\unicode[STIX]{x1D6FC}]$
for the
$[\unicode[STIX]{x1D6FC}]$
for the
![]() $\unicode[STIX]{x1D6E4}$
-orbit of a character
$\unicode[STIX]{x1D6E4}$
-orbit of a character
![]() $\unicode[STIX]{x1D6FC}\in \text{X}$
. The following result (see Proposition 8.8), which again is proved via modular methods, suggests that in order to determine the permutation
$\unicode[STIX]{x1D6FC}\in \text{X}$
. The following result (see Proposition 8.8), which again is proved via modular methods, suggests that in order to determine the permutation
![]() $\unicode[STIX]{x1D6F6}$
it is sufficient to compute the value of
$\unicode[STIX]{x1D6F6}$
it is sufficient to compute the value of
![]() $\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FC}])$
for certain characters
$\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FC}])$
for certain characters
![]() $\unicode[STIX]{x1D6FC}$
only.
$\unicode[STIX]{x1D6FC}$
only.
Proposition. Let
![]() $\unicode[STIX]{x1D6FC}\in \text{X}$
and let
$\unicode[STIX]{x1D6FC}\in \text{X}$
and let
![]() $\boldsymbol{l}$
be the unique subfield of
$\boldsymbol{l}$
be the unique subfield of
![]() $\boldsymbol{k}$
such that the stabilizer of
$\boldsymbol{k}$
such that the stabilizer of
![]() $\unicode[STIX]{x1D6FC}$
in
$\unicode[STIX]{x1D6FC}$
in
![]() $\unicode[STIX]{x1D6E4}$
is
$\unicode[STIX]{x1D6E4}$
is
![]() $\text{Gal}(\boldsymbol{k}/\boldsymbol{l})$
. Suppose that there are a
$\text{Gal}(\boldsymbol{k}/\boldsymbol{l})$
. Suppose that there are a
![]() $\unicode[STIX]{x1D6E4}$
-regular character
$\unicode[STIX]{x1D6E4}$
-regular character
![]() $\unicode[STIX]{x1D6FD}\in \text{X}$
and a prime number
$\unicode[STIX]{x1D6FD}\in \text{X}$
and a prime number
![]() $\ell \neq p$
prime to the order of
$\ell \neq p$
prime to the order of
![]() $\boldsymbol{l}^{\times }$
such that the order of
$\boldsymbol{l}^{\times }$
such that the order of
![]() $\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}^{-1}$
is a power of
$\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}^{-1}$
is a power of
![]() $\ell$
. Suppose further that
$\ell$
. Suppose further that
![]() $\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FD}])=[\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D707}]$
for some character
$\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FD}])=[\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D707}]$
for some character
![]() $\unicode[STIX]{x1D707}\in \text{X}$
. Then
$\unicode[STIX]{x1D707}\in \text{X}$
. Then
![]() $\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FC}])=[\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D708}]$
, where
$\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FC}])=[\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D708}]$
, where
![]() $\unicode[STIX]{x1D708}\in \text{X}$
is the unique character of order prime to
$\unicode[STIX]{x1D708}\in \text{X}$
is the unique character of order prime to
![]() $\ell$
such that
$\ell$
such that
![]() $\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}^{-1}$
has order a power of
$\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}^{-1}$
has order a power of
![]() $\ell$
.
$\ell$
.
In fact we need a more powerful version of this result, which we do not explain here, that requires being able to pass from
![]() $\text{G}$
to a bigger group
$\text{G}$
to a bigger group
![]() $\text{GL}_{m\text{sp}\prime }(\text{D})$
, with
$\text{GL}_{m\text{sp}\prime }(\text{D})$
, with
![]() $m\text{sp}\prime >m$
. (See § 8, in particular § 8.3.)
$m\text{sp}\prime >m$
. (See § 8, in particular § 8.3.)
To conclude, in the final section of the paper we illustrate this principle in the essentially tame case. We start from the Parametrization Theorem [Reference Bushnell and HenniartBH11a, 6.1], which gives a canonical bijection
between isomorphism classes of admissible pairs of degree
![]() $n$
and isomorphism classes of essentially tame cuspidal irreducible representations of
$n$
and isomorphism classes of essentially tame cuspidal irreducible representations of
![]() $\text{G}$
of parametric degree
$\text{G}$
of parametric degree
![]() $n$
. The First Comparison Theorem [Reference Bushnell and HenniartBH11a, 6.1] shows how to translate the Jacquet–Langlands correspondence for these cuspidal representations in terms of admissible pairs: for any admissible pair
$n$
. The First Comparison Theorem [Reference Bushnell and HenniartBH11a, 6.1] shows how to translate the Jacquet–Langlands correspondence for these cuspidal representations in terms of admissible pairs: for any admissible pair
![]() $(\text{L}/\text{F},\unicode[STIX]{x1D709})$
of degree
$(\text{L}/\text{F},\unicode[STIX]{x1D709})$
of degree
![]() $n$
, there is a canonically determined tamely ramified character
$n$
, there is a canonically determined tamely ramified character
![]() $\unicode[STIX]{x1D708}$
of
$\unicode[STIX]{x1D708}$
of
![]() $\text{L}^{\times }$
such that
$\text{L}^{\times }$
such that
![]() $\unicode[STIX]{x1D708}^{2}=1$
and
$\unicode[STIX]{x1D708}^{2}=1$
and
We show that, for appropriate choices, this result can be rephrased in terms of our
![]() $\unicode[STIX]{x1D6FC}$
-parameters and gives us an explicit formula for
$\unicode[STIX]{x1D6FC}$
-parameters and gives us an explicit formula for
![]() $\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FC}])$
for all
$\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FC}])$
for all
![]() $\unicode[STIX]{x1D6E4}$
-regular characters
$\unicode[STIX]{x1D6E4}$
-regular characters
![]() $\unicode[STIX]{x1D6FC}\in \text{X}$
. Applying the proposition above, we then prove that this explicit formula actually holds for any
$\unicode[STIX]{x1D6FC}\in \text{X}$
. Applying the proposition above, we then prove that this explicit formula actually holds for any
![]() $\unicode[STIX]{x1D6FC}\in \text{X}$
.
$\unicode[STIX]{x1D6FC}\in \text{X}$
.
As in [Reference Bushnell and HenniartBH11a], we formulate our result in terms of admissible pairs. We first define a bijection
between inertial classes of admissible pairs (see Definition 9.5) of degree dividing
![]() $n$
and inertial classes of discrete series representations of
$n$
and inertial classes of discrete series representations of
![]() $\text{G}$
with essentially tame endo-class, extending (1.2) up to inertia. In the case where
$\text{G}$
with essentially tame endo-class, extending (1.2) up to inertia. In the case where
![]() $\text{G}$
is the group
$\text{G}$
is the group
![]() $\text{H}$
, this bijection is canonical, but for a general
$\text{H}$
, this bijection is canonical, but for a general
![]() $\text{G}$
it depends a priori on various choices. We prove the following result (see Theorem 9.13).
$\text{G}$
it depends a priori on various choices. We prove the following result (see Theorem 9.13).
Theorem D. Let
![]() $[\text{L}/\text{F},\unicode[STIX]{x1D709}]$
be an inertial class of admissible pairs of degree dividing
$[\text{L}/\text{F},\unicode[STIX]{x1D709}]$
be an inertial class of admissible pairs of degree dividing
![]() $n$
. There is a canonically determined tamely ramified character
$n$
. There is a canonically determined tamely ramified character
![]() $\unicode[STIX]{x1D707}$
of the group of units of the ring of integers of
$\unicode[STIX]{x1D707}$
of the group of units of the ring of integers of
![]() $\text{L}$
such that
$\text{L}$
such that
![]() $\unicode[STIX]{x1D707}^{2}=1$
and
$\unicode[STIX]{x1D707}^{2}=1$
and
We thus deduce a posteriori that our bijection (1.3) is canonical, that is, it does not depend on the various choices we have made (see Remark 9.15).
Remark.
After this paper was written, Dotto proved the Endo-class Invariance Conjecture in [Reference DottoDot17], using methods developed here and in [Reference Bushnell and HenniartBH11a]. He goes further and gives an explicit description of the Jacquet–Langlands correspondence up to inertia.
2 Notation
We fix a non-Archimedean locally compact field
![]() $\text{F}$
with residual characteristic
$\text{F}$
with residual characteristic
![]() $p$
. Write
$p$
. Write
![]() $q$
for the cardinality of the residue field of
$q$
for the cardinality of the residue field of
![]() $\text{F}$
.
$\text{F}$
.
Given a finite-dimensional central division
![]() $\text{F}$
-algebra
$\text{F}$
-algebra
![]() $\text{D}$
and a positive integer
$\text{D}$
and a positive integer
![]() $m\geqslant 1$
, we write
$m\geqslant 1$
, we write
![]() $\text{M}_{m}(\text{D})$
for the algebra of
$\text{M}_{m}(\text{D})$
for the algebra of
![]() $m\times m$
matrices with coefficients in
$m\times m$
matrices with coefficients in
![]() $\text{D}$
and
$\text{D}$
and
![]() $\text{GL}_{m}(\text{D})$
for the group of its invertible elements. Choose an
$\text{GL}_{m}(\text{D})$
for the group of its invertible elements. Choose an
![]() $m\geqslant 1$
and write
$m\geqslant 1$
and write
![]() $\text{G}=\text{GL}_{m}(\text{D})$
. Write
$\text{G}=\text{GL}_{m}(\text{D})$
. Write
![]() $d$
for the reduced degree of
$d$
for the reduced degree of
![]() $\text{D}$
over
$\text{D}$
over
![]() $\text{F}$
, and define
$\text{F}$
, and define
![]() $n=md$
.
$n=md$
.
Given an algebraically closed field
![]() $\text{R}$
of characteristic different from
$\text{R}$
of characteristic different from
![]() $p$
, we will consider smooth representations of the locally profinite group
$p$
, we will consider smooth representations of the locally profinite group
![]() $\text{G}$
with coefficients in
$\text{G}$
with coefficients in
![]() $\text{R}$
. We write
$\text{R}$
. We write
![]() $\text{Irr}(\text{G},\text{R})$
for the set of isomorphism classes of irreducible representations of
$\text{Irr}(\text{G},\text{R})$
for the set of isomorphism classes of irreducible representations of
![]() $\text{G}$
and
$\text{G}$
and
![]() $\mathscr{R}(\text{G},\text{R})$
for the Grothendieck group of its finite-length representations, identified with the free abelian group with basis
$\mathscr{R}(\text{G},\text{R})$
for the Grothendieck group of its finite-length representations, identified with the free abelian group with basis
![]() $\text{Irr}(\text{G},\text{R})$
. If
$\text{Irr}(\text{G},\text{R})$
. If
![]() $\unicode[STIX]{x1D70B}$
is a representation of
$\unicode[STIX]{x1D70B}$
is a representation of
![]() $\text{G}$
, the integer
$\text{G}$
, the integer
![]() $m$
is called its degree.
$m$
is called its degree.
Given
![]() $\unicode[STIX]{x1D6FC}=(m_{1},\ldots ,m_{r})$
a family of positive integers with sum
$\unicode[STIX]{x1D6FC}=(m_{1},\ldots ,m_{r})$
a family of positive integers with sum
![]() $m$
, we write
$m$
, we write
![]() $\boldsymbol{i}_{\unicode[STIX]{x1D6FC}}$
for the functor of standard parabolic induction associated with
$\boldsymbol{i}_{\unicode[STIX]{x1D6FC}}$
for the functor of standard parabolic induction associated with
![]() $\unicode[STIX]{x1D6FC}$
, normalized with respect to the choice of a square root in the field
$\unicode[STIX]{x1D6FC}$
, normalized with respect to the choice of a square root in the field
![]() $\text{R}$
of the cardinality
$\text{R}$
of the cardinality
![]() $q$
of the residual field of
$q$
of the residual field of
![]() $\text{F}$
. Given, for each
$\text{F}$
. Given, for each
![]() $i\in \{1,\ldots ,r\}$
, a representation
$i\in \{1,\ldots ,r\}$
, a representation
![]() $\unicode[STIX]{x1D70B}_{i}$
of
$\unicode[STIX]{x1D70B}_{i}$
of
![]() $\text{GL}_{m_{i}}(\text{D})$
, we write
$\text{GL}_{m_{i}}(\text{D})$
, we write
Given a representation
![]() $\unicode[STIX]{x1D70B}$
and a character
$\unicode[STIX]{x1D70B}$
and a character
![]() $\unicode[STIX]{x1D712}$
of
$\unicode[STIX]{x1D712}$
of
![]() $\text{G}$
, we write
$\text{G}$
, we write
![]() $\unicode[STIX]{x1D70B}\unicode[STIX]{x1D712}$
for the twisted representation defined by
$\unicode[STIX]{x1D70B}\unicode[STIX]{x1D712}$
for the twisted representation defined by
![]() $g\mapsto \unicode[STIX]{x1D712}(g)\unicode[STIX]{x1D70B}(g)$
.
$g\mapsto \unicode[STIX]{x1D712}(g)\unicode[STIX]{x1D70B}(g)$
.
We fix once and for all a smooth additive character
![]() $\unicode[STIX]{x1D713}:\text{F}\rightarrow \text{R}^{\times }$
, trivial on the maximal ideal
$\unicode[STIX]{x1D713}:\text{F}\rightarrow \text{R}^{\times }$
, trivial on the maximal ideal
![]() $\mathfrak{p}$
of the ring of integers
$\mathfrak{p}$
of the ring of integers
![]() $\mathscr{O}$
of
$\mathscr{O}$
of
![]() $\text{F}$
but not trivial on
$\text{F}$
but not trivial on
![]() $\mathscr{O}$
.
$\mathscr{O}$
.
We write
![]() $\unicode[STIX]{x1D708}$
for the unramified
$\unicode[STIX]{x1D708}$
for the unramified
![]() $\text{R}$
-character of
$\text{R}$
-character of
![]() $\text{G}$
given by composing the reduced norm from
$\text{G}$
given by composing the reduced norm from
![]() $\text{G}$
to
$\text{G}$
to
![]() $\text{F}^{\times }$
with the absolute value of
$\text{F}^{\times }$
with the absolute value of
![]() $\text{F}$
which takes any uniformizer to the inverse of
$\text{F}$
which takes any uniformizer to the inverse of
![]() $q$
in
$q$
in
![]() $\text{R}$
.
$\text{R}$
.
3 Preliminaries
In this section, we let
![]() $\text{R}$
be an algebraically closed field of characteristic different from
$\text{R}$
be an algebraically closed field of characteristic different from
![]() $p$
.
$p$
.
3.1
Let
![]() $\unicode[STIX]{x1D70C}$
be a cuspidal irreducible
$\unicode[STIX]{x1D70C}$
be a cuspidal irreducible
![]() $\text{R}$
-representation of
$\text{R}$
-representation of
![]() $\text{G}$
. Associated with
$\text{G}$
. Associated with
![]() $\unicode[STIX]{x1D70C}$
, there is a positive integer
$\unicode[STIX]{x1D70C}$
, there is a positive integer
![]() $s(\unicode[STIX]{x1D70C})$
defined in [Reference Mínguez and SécherreMS14b, § 3.4] (see also Remark 3.8). When
$s(\unicode[STIX]{x1D70C})$
defined in [Reference Mínguez and SécherreMS14b, § 3.4] (see also Remark 3.8). When
![]() $\text{R}$
is the field of complex numbers,
$\text{R}$
is the field of complex numbers,
![]() $s(\unicode[STIX]{x1D70C})$
is the unique positive integer
$s(\unicode[STIX]{x1D70C})$
is the unique positive integer
![]() $k$
such that
$k$
such that
![]() $\unicode[STIX]{x1D70C}\times \unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}^{k}$
is reducible, and it is related to the parametric degree
$\unicode[STIX]{x1D70C}\times \unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}^{k}$
is reducible, and it is related to the parametric degree
![]() $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70C})$
defined in [Reference Bushnell and HenniartBH11a, § 2] by the formula
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70C})$
defined in [Reference Bushnell and HenniartBH11a, § 2] by the formula
![]() $s(\unicode[STIX]{x1D70C})\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70C})=n$
. For the general case, see Remark 3.8.
$s(\unicode[STIX]{x1D70C})\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70C})=n$
. For the general case, see Remark 3.8.
In [Reference Mínguez and SécherreMS14a] we attach to
![]() $\unicode[STIX]{x1D70C}$
and any integer
$\unicode[STIX]{x1D70C}$
and any integer
![]() $r\geqslant 1$
an irreducible subrepresentation
$r\geqslant 1$
an irreducible subrepresentation
![]() $\text{Z}(\unicode[STIX]{x1D70C},r)$
and an irreducible quotient
$\text{Z}(\unicode[STIX]{x1D70C},r)$
and an irreducible quotient
![]() $\text{L}(\unicode[STIX]{x1D70C},r)$
of the induced representation
$\text{L}(\unicode[STIX]{x1D70C},r)$
of the induced representation
(see [Reference Mínguez and SécherreMS14a, Paragraph 7.2 and Définition 7.5]), where
![]() $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70C}}$
is the character
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70C}}$
is the character
![]() $\unicode[STIX]{x1D708}^{s(\unicode[STIX]{x1D70C})}$
.
$\unicode[STIX]{x1D708}^{s(\unicode[STIX]{x1D70C})}$
.
When
![]() $\text{R}$
is the field of complex numbers,
$\text{R}$
is the field of complex numbers,
![]() $\text{Z}(\unicode[STIX]{x1D70C},r)$
and
$\text{Z}(\unicode[STIX]{x1D70C},r)$
and
![]() $\text{L}(\unicode[STIX]{x1D70C},r)$
are uniquely determined in this way, and all essentially square-integrable representations of
$\text{L}(\unicode[STIX]{x1D70C},r)$
are uniquely determined in this way, and all essentially square-integrable representations of
![]() $\text{G}$
are isomorphic to a representation of the form
$\text{G}$
are isomorphic to a representation of the form
![]() $\text{L}(\unicode[STIX]{x1D70C},r)$
for a unique pair
$\text{L}(\unicode[STIX]{x1D70C},r)$
for a unique pair
![]() $(\unicode[STIX]{x1D70C},r)$
.
$(\unicode[STIX]{x1D70C},r)$
.
For an arbitrary
![]() $\text{R}$
, the representation
$\text{R}$
, the representation
![]() $\text{L}(\unicode[STIX]{x1D70C},r)$
is called a discrete series
$\text{L}(\unicode[STIX]{x1D70C},r)$
is called a discrete series
![]() $\text{R}$
-representation of
$\text{R}$
-representation of
![]() $\text{G}$
, and
$\text{G}$
, and
![]() $\text{Z}(\unicode[STIX]{x1D70C},r)$
is called a Speh
$\text{Z}(\unicode[STIX]{x1D70C},r)$
is called a Speh
![]() $\text{R}$
-representation. If
$\text{R}$
-representation. If
![]() $\unicode[STIX]{x1D70C}$
is supercuspidal,
$\unicode[STIX]{x1D70C}$
is supercuspidal,
![]() $\text{Z}(\unicode[STIX]{x1D70C},r)$
is called a super-Speh representation.
$\text{Z}(\unicode[STIX]{x1D70C},r)$
is called a super-Speh representation.
According to [Reference Mínguez and SécherreMS14a, § 8.1], where the notion of residually nondegenerate representation is defined, the induced representation (3.1) contains a unique residually nondegenerate irreducible subquotient, denoted by
When
![]() $\text{R}$
has characteristic
$\text{R}$
has characteristic
![]() $0$
, this is equal to
$0$
, this is equal to
![]() $\text{L}(\unicode[STIX]{x1D70C},r)$
. When
$\text{L}(\unicode[STIX]{x1D70C},r)$
. When
![]() $\text{R}$
has characteristic
$\text{R}$
has characteristic
![]() $\ell >0$
, however, it may differ from
$\ell >0$
, however, it may differ from
![]() $\text{L}(\unicode[STIX]{x1D70C},r)$
(see [Reference Mínguez and SécherreMS14a, Remark 8.14]).
$\text{L}(\unicode[STIX]{x1D70C},r)$
(see [Reference Mínguez and SécherreMS14a, Remark 8.14]).
Assume that
![]() $\text{R}$
has characteristic
$\text{R}$
has characteristic
![]() $\ell >0$
, and write
$\ell >0$
, and write
![]() $\unicode[STIX]{x1D714}(\unicode[STIX]{x1D70C})$
for the smallest positive integer
$\unicode[STIX]{x1D714}(\unicode[STIX]{x1D70C})$
for the smallest positive integer
![]() $i\geqslant 1$
such that
$i\geqslant 1$
such that
![]() $\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70C}}^{i}$
is isomorphic to
$\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70C}}^{i}$
is isomorphic to
![]() $\unicode[STIX]{x1D70C}$
. Then the irreducible representation
$\unicode[STIX]{x1D70C}$
. Then the irreducible representation
is cuspidal for any integer
![]() $v\geqslant 0$
. Moreover, any cuspidal non-supercuspidal irreducible representation is of the form (3.2) for a supercuspidal irreducible representation
$v\geqslant 0$
. Moreover, any cuspidal non-supercuspidal irreducible representation is of the form (3.2) for a supercuspidal irreducible representation
![]() $\unicode[STIX]{x1D70C}$
and a unique integer
$\unicode[STIX]{x1D70C}$
and a unique integer
![]() $v\geqslant 0$
(see [Reference Mínguez and SécherreMS14a, Théorème 6.14]). We record this latter fact for future reference.
$v\geqslant 0$
(see [Reference Mínguez and SécherreMS14a, Théorème 6.14]). We record this latter fact for future reference.
Proposition 3.1. Assume that
![]() $\text{R}$
has positive characteristic
$\text{R}$
has positive characteristic
![]() $\ell$
, and let
$\ell$
, and let
![]() $\unicode[STIX]{x1D70C}$
be a cuspidal irreducible representation of
$\unicode[STIX]{x1D70C}$
be a cuspidal irreducible representation of
![]() $\text{G}$
. There exist a unique positive integer
$\text{G}$
. There exist a unique positive integer
![]() $k=k(\unicode[STIX]{x1D70C})$
and a supercuspidal irreducible representation
$k=k(\unicode[STIX]{x1D70C})$
and a supercuspidal irreducible representation
![]() $\unicode[STIX]{x1D70F}$
of degree
$\unicode[STIX]{x1D70F}$
of degree
![]() $m/k$
such that
$m/k$
such that
![]() $\unicode[STIX]{x1D70C}$
is isomorphic to
$\unicode[STIX]{x1D70C}$
is isomorphic to
![]() $\text{Sp}(\unicode[STIX]{x1D70F},k)$
.
$\text{Sp}(\unicode[STIX]{x1D70F},k)$
.
3.2
In this subsection, we assume that
![]() $\text{R}$
is an algebraic closure
$\text{R}$
is an algebraic closure
![]() $\overline{\mathbf{Q}}_{\ell }$
of the field of
$\overline{\mathbf{Q}}_{\ell }$
of the field of
![]() $\ell$
-adic numbers. Recall (see [Reference VignérasVig96]) that an irreducible
$\ell$
-adic numbers. Recall (see [Reference VignérasVig96]) that an irreducible
![]() $\ell$
-adic representation of
$\ell$
-adic representation of
![]() $\text{G}$
is integral if it contains a
$\text{G}$
is integral if it contains a
![]() $\text{G}$
-stable
$\text{G}$
-stable
![]() $\overline{\mathbf{Z}}_{\ell }$
-lattice. Let
$\overline{\mathbf{Z}}_{\ell }$
-lattice. Let
![]() $\widetilde{\unicode[STIX]{x1D70C}}$
be an
$\widetilde{\unicode[STIX]{x1D70C}}$
be an
![]() $\ell$
-adic cuspidal irreducible representation of
$\ell$
-adic cuspidal irreducible representation of
![]() $\text{G}$
. By [Reference VignérasVig96, II.4.12], it is integral if and only if its central character has values in
$\text{G}$
. By [Reference VignérasVig96, II.4.12], it is integral if and only if its central character has values in
![]() $\overline{\mathbf{Z}}_{\ell }$
. In particular, there is always an unramified twist of
$\overline{\mathbf{Z}}_{\ell }$
. In particular, there is always an unramified twist of
![]() $\widetilde{\unicode[STIX]{x1D70C}}$
which is integral.
$\widetilde{\unicode[STIX]{x1D70C}}$
which is integral.
Assume that
![]() $\widetilde{\unicode[STIX]{x1D70C}}$
is integral and write
$\widetilde{\unicode[STIX]{x1D70C}}$
is integral and write
![]() $a=a(\widetilde{\unicode[STIX]{x1D70C}})$
for the length of its reduction mod
$a=a(\widetilde{\unicode[STIX]{x1D70C}})$
for the length of its reduction mod
![]() $\ell$
, denoted by
$\ell$
, denoted by
![]() $\text{}\text{r}_{\ell }(\widetilde{\unicode[STIX]{x1D70C}})$
.
$\text{}\text{r}_{\ell }(\widetilde{\unicode[STIX]{x1D70C}})$
.
Proposition 3.2 [Reference Mínguez and SécherreMS14b, Theorem 3.15].
Let
![]() $\unicode[STIX]{x1D70C}$
be an irreducible factor of
$\unicode[STIX]{x1D70C}$
be an irreducible factor of
![]() $\text{}\text{r}_{\ell }(\widetilde{\unicode[STIX]{x1D70C}})$
. Then
$\text{}\text{r}_{\ell }(\widetilde{\unicode[STIX]{x1D70C}})$
. Then
where
![]() $\unicode[STIX]{x1D708}$
denotes the unramified mod-
$\unicode[STIX]{x1D708}$
denotes the unramified mod-
![]() $\ell$
character ‘absolute value of the reduced norm’.
$\ell$
character ‘absolute value of the reduced norm’.
3.3
We recall briefly the language of simple strata, though we do not require much of the detail of the constructions. For a detailed presentation, see [Reference SécherreSéc05b, Reference Mínguez and SécherreMS14b]. For simple strata, we use the simplified notation of [Reference Bushnell and HenniartBH14, ch. 2].
Let
![]() $[\mathfrak{a},\unicode[STIX]{x1D6FD}]$
be a simple stratum in the simple central
$[\mathfrak{a},\unicode[STIX]{x1D6FD}]$
be a simple stratum in the simple central
![]() $\text{F}$
-algebra
$\text{F}$
-algebra
![]() $\text{M}_{m}(\text{D})$
. Rather than giving the precise definition, we simply recall that it is composed of an element
$\text{M}_{m}(\text{D})$
. Rather than giving the precise definition, we simply recall that it is composed of an element
![]() $\unicode[STIX]{x1D6FD}\in \text{M}_{m}(\text{D})$
such that the
$\unicode[STIX]{x1D6FD}\in \text{M}_{m}(\text{D})$
such that the
![]() $\text{F}$
-algebra
$\text{F}$
-algebra
![]() $\text{F}[\unicode[STIX]{x1D6FD}]$
is a field and a hereditary order
$\text{F}[\unicode[STIX]{x1D6FD}]$
is a field and a hereditary order
![]() $\mathfrak{a}\subseteq \text{M}_{m}(\text{D})$
normalized by
$\mathfrak{a}\subseteq \text{M}_{m}(\text{D})$
normalized by
![]() $\text{F}[\unicode[STIX]{x1D6FD}]^{\times }$
. The centralizer of
$\text{F}[\unicode[STIX]{x1D6FD}]^{\times }$
. The centralizer of
![]() $\unicode[STIX]{x1D6FD}$
in
$\unicode[STIX]{x1D6FD}$
in
![]() $\text{M}_{m}(\text{D})$
, denoted by
$\text{M}_{m}(\text{D})$
, denoted by
![]() $\text{B}$
, is a simple central
$\text{B}$
, is a simple central
![]() $\text{F}[\unicode[STIX]{x1D6FD}]$
-algebra. There are an
$\text{F}[\unicode[STIX]{x1D6FD}]$
-algebra. There are an
![]() $\text{F}[\unicode[STIX]{x1D6FD}]$
-division algebra
$\text{F}[\unicode[STIX]{x1D6FD}]$
-division algebra
![]() $\text{D}\text{sp}\prime$
and an integer
$\text{D}\text{sp}\prime$
and an integer
![]() $m\text{sp}\prime \geqslant 1$
such that
$m\text{sp}\prime \geqslant 1$
such that
The intersection
![]() $\mathfrak{b}=\mathfrak{a}\,\cap \,\text{B}$
is a hereditary order in
$\mathfrak{b}=\mathfrak{a}\,\cap \,\text{B}$
is a hereditary order in
![]() $\text{B}$
.
$\text{B}$
.
Recall [Reference SécherreSéc04, Reference Mínguez and SécherreMS14b] that associated with
![]() $[\mathfrak{a},\unicode[STIX]{x1D6FD}]$
are compact open subgroups
$[\mathfrak{a},\unicode[STIX]{x1D6FD}]$
are compact open subgroups
of
![]() $\text{G}$
, together with a non-empty finite set
$\text{G}$
, together with a non-empty finite set
![]() $\mathscr{C}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
depending on the choice of
$\mathscr{C}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
depending on the choice of
![]() $\unicode[STIX]{x1D713}$
made in § 2. These groups are normal in
$\unicode[STIX]{x1D713}$
made in § 2. These groups are normal in
![]() $\text{J}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
, and the elements of
$\text{J}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
, and the elements of
![]() $\mathscr{C}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
are
$\mathscr{C}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
are
![]() $\text{R}$
-characters of
$\text{R}$
-characters of
![]() $\text{H}^{1}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
, called simple characters. Besides,
$\text{H}^{1}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
, called simple characters. Besides,
![]() $\text{H}^{1}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
and
$\text{H}^{1}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
and
![]() $\text{J}^{1}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
are pro-
$\text{J}^{1}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
are pro-
![]() $p$
-groups, and
$p$
-groups, and
![]() $\text{J}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
is equal to
$\text{J}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
is equal to
![]() $\mathfrak{b}^{\times }\text{J}^{1}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
.
$\mathfrak{b}^{\times }\text{J}^{1}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
.
Attached to a simple character
![]() $\unicode[STIX]{x1D703}\in \mathscr{C}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
is an invariant called its endo-class. We do not recall the precise definition of this invariant, which can be found in [Reference Bushnell and HenniartBH96, Reference Broussous, Sécherre and StevensBSS12]. We only need a few properties of endo-classes, which we will recall when they are needed. Endo-classes form a set
$\unicode[STIX]{x1D703}\in \mathscr{C}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
is an invariant called its endo-class. We do not recall the precise definition of this invariant, which can be found in [Reference Bushnell and HenniartBH96, Reference Broussous, Sécherre and StevensBSS12]. We only need a few properties of endo-classes, which we will recall when they are needed. Endo-classes form a set
![]() $\mathscr{E}(\text{F})$
which depends only on
$\mathscr{E}(\text{F})$
which depends only on
![]() $\text{F}$
.
$\text{F}$
.
Lemma 3.3 [Reference Broussous, Sécherre and StevensBSS12, Lemma 4.7].
Given a simple character
![]() $\unicode[STIX]{x1D703}\in \mathscr{C}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
with endo-class
$\unicode[STIX]{x1D703}\in \mathscr{C}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
, the degree, ramification index and residue degree of
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
, the degree, ramification index and residue degree of
![]() $\text{F}[\unicode[STIX]{x1D6FD}]$
over
$\text{F}[\unicode[STIX]{x1D6FD}]$
over
![]() $\text{F}$
depend only on
$\text{F}$
depend only on
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
. These integers are called the degree, the ramification index and the residue degree of
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
. These integers are called the degree, the ramification index and the residue degree of
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
, respectively.
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
, respectively.
The endo-class of a simple character in
![]() $\text{G}$
has degree dividing
$\text{G}$
has degree dividing
![]() $n$
. Conversely, any endo-class of degree dividing
$n$
. Conversely, any endo-class of degree dividing
![]() $n$
occurs as the endo-class of some simple character in
$n$
occurs as the endo-class of some simple character in
![]() $\text{G}$
.
$\text{G}$
.
A
![]() $\unicode[STIX]{x1D6FD}$
-extension of a simple character
$\unicode[STIX]{x1D6FD}$
-extension of a simple character
![]() $\unicode[STIX]{x1D703}\in \mathscr{C}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
is an irreducible representation of
$\unicode[STIX]{x1D703}\in \mathscr{C}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
is an irreducible representation of
![]() $\text{J}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
with coefficients in
$\text{J}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
with coefficients in
![]() $\text{R}$
whose restriction to
$\text{R}$
whose restriction to
![]() $\text{J}^{1}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
is irreducible, whose restriction to
$\text{J}^{1}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
is irreducible, whose restriction to
![]() $\text{H}^{1}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
contains
$\text{H}^{1}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
contains
![]() $\unicode[STIX]{x1D703}$
and which is intertwined by any element of
$\unicode[STIX]{x1D703}$
and which is intertwined by any element of
![]() $\text{B}^{\times }$
(see [Reference SécherreSéc05a, Reference Mínguez and SécherreMS14b]).
$\text{B}^{\times }$
(see [Reference SécherreSéc05a, Reference Mínguez and SécherreMS14b]).
Assume now that
![]() $\mathfrak{b}$
is a maximal order in
$\mathfrak{b}$
is a maximal order in
![]() $\text{B}$
, in which case we say that the simple stratum
$\text{B}$
, in which case we say that the simple stratum
![]() $[\mathfrak{a},\unicode[STIX]{x1D6FD}]$
, the simple characters in
$[\mathfrak{a},\unicode[STIX]{x1D6FD}]$
, the simple characters in
![]() $\mathscr{C}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
and their
$\mathscr{C}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
and their
![]() $\unicode[STIX]{x1D6FD}$
-extensions are maximal. Let us fix an isomorphism (3.3) such that the image of
$\unicode[STIX]{x1D6FD}$
-extensions are maximal. Let us fix an isomorphism (3.3) such that the image of
![]() $\mathfrak{b}$
is the maximal order made of all matrices with integer entries. There is a natural group isomorphism
$\mathfrak{b}$
is the maximal order made of all matrices with integer entries. There is a natural group isomorphism
where
![]() $\boldsymbol{d}$
is the residue field of
$\boldsymbol{d}$
is the residue field of
![]() $\text{D}\text{sp}\prime$
. We write
$\text{D}\text{sp}\prime$
. We write
![]() $\mathscr{G}$
for the group on the right-hand side. Let us fix a
$\mathscr{G}$
for the group on the right-hand side. Let us fix a
![]() $\unicode[STIX]{x1D6FD}$
-extension
$\unicode[STIX]{x1D6FD}$
-extension
![]() $\unicode[STIX]{x1D705}$
of some simple character
$\unicode[STIX]{x1D705}$
of some simple character
![]() $\unicode[STIX]{x1D703}\in \mathscr{C}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
. We write
$\unicode[STIX]{x1D703}\in \mathscr{C}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
. We write
![]() $\text{J}=\text{J}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
and
$\text{J}=\text{J}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
and
![]() $\text{J}^{1}=\text{J}^{1}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
.
$\text{J}^{1}=\text{J}^{1}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
.
We fix a finite extension
![]() $\boldsymbol{k}$
of
$\boldsymbol{k}$
of
![]() $\boldsymbol{d}$
of degree
$\boldsymbol{d}$
of degree
![]() $m\text{sp}\prime$
. We write
$m\text{sp}\prime$
. We write
![]() $\unicode[STIX]{x1D6F4}$
for the Galois group of this extension and
$\unicode[STIX]{x1D6F4}$
for the Galois group of this extension and
![]() $\text{X}$
for the group of
$\text{X}$
for the group of
![]() $\text{R}$
-characters of
$\text{R}$
-characters of
![]() $\boldsymbol{k}^{\times }$
. Given
$\boldsymbol{k}^{\times }$
. Given
![]() $\unicode[STIX]{x1D6FC}\in \text{X}$
, there is a unique subfield
$\unicode[STIX]{x1D6FC}\in \text{X}$
, there is a unique subfield
![]() $\boldsymbol{d}\subseteq \boldsymbol{d}[\unicode[STIX]{x1D6FC}]\subseteq \boldsymbol{k}$
such that the
$\boldsymbol{d}\subseteq \boldsymbol{d}[\unicode[STIX]{x1D6FC}]\subseteq \boldsymbol{k}$
such that the
![]() $\unicode[STIX]{x1D6F4}$
-stabilizer of
$\unicode[STIX]{x1D6F4}$
-stabilizer of
![]() $\unicode[STIX]{x1D6FC}$
is
$\unicode[STIX]{x1D6FC}$
is
![]() $\text{Gal}(\boldsymbol{k}/\boldsymbol{d}[\unicode[STIX]{x1D6FC}])$
, and then a character
$\text{Gal}(\boldsymbol{k}/\boldsymbol{d}[\unicode[STIX]{x1D6FC}])$
, and then a character
![]() $\unicode[STIX]{x1D6FC}_{0}$
of
$\unicode[STIX]{x1D6FC}_{0}$
of
![]() $\boldsymbol{d}[\unicode[STIX]{x1D6FC}]^{\times }$
such that
$\boldsymbol{d}[\unicode[STIX]{x1D6FC}]^{\times }$
such that
![]() $\unicode[STIX]{x1D6FC}$
is equal to
$\unicode[STIX]{x1D6FC}$
is equal to
![]() $\unicode[STIX]{x1D6FC}_{0}$
composed with the norm of
$\unicode[STIX]{x1D6FC}_{0}$
composed with the norm of
![]() $\boldsymbol{k}$
over
$\boldsymbol{k}$
over
![]() $\boldsymbol{d}[\unicode[STIX]{x1D6FC}]$
. If we write
$\boldsymbol{d}[\unicode[STIX]{x1D6FC}]$
. If we write
![]() $u$
for the degree of
$u$
for the degree of
![]() $\boldsymbol{d}[\unicode[STIX]{x1D6FC}]$
over
$\boldsymbol{d}[\unicode[STIX]{x1D6FC}]$
over
![]() $\boldsymbol{d}$
, then
$\boldsymbol{d}$
, then
![]() $\unicode[STIX]{x1D6FC}_{0}$
defines a supercuspidal irreducible
$\unicode[STIX]{x1D6FC}_{0}$
defines a supercuspidal irreducible
![]() $\text{R}$
-representation
$\text{R}$
-representation
![]() $\unicode[STIX]{x1D70E}_{0}$
of
$\unicode[STIX]{x1D70E}_{0}$
of
![]() $\text{GL}_{u}(\boldsymbol{d})$
; see [Reference GreenGre96] for the case where
$\text{GL}_{u}(\boldsymbol{d})$
; see [Reference GreenGre96] for the case where
![]() $\text{R}$
has characteristic
$\text{R}$
has characteristic
![]() $0$
, and [Reference DipperDip85] or [Reference Mínguez and SécherreMS15] otherwise.
$0$
, and [Reference DipperDip85] or [Reference Mínguez and SécherreMS15] otherwise.
Remark 3.4. More precisely, if
![]() $\text{R}$
has characteristic
$\text{R}$
has characteristic
![]() $0$
, fix an embedding of
$0$
, fix an embedding of
![]() $\boldsymbol{d}[\unicode[STIX]{x1D6FC}]$
in
$\boldsymbol{d}[\unicode[STIX]{x1D6FC}]$
in
![]() $\text{M}_{u}(\boldsymbol{d})$
. Then
$\text{M}_{u}(\boldsymbol{d})$
. Then
![]() $\unicode[STIX]{x1D70E}_{0}$
is the unique (up to isomorphism) irreducible representation of
$\unicode[STIX]{x1D70E}_{0}$
is the unique (up to isomorphism) irreducible representation of
![]() $\text{GL}_{u}(\boldsymbol{d})$
such that
$\text{GL}_{u}(\boldsymbol{d})$
such that
for all
![]() $g\in \boldsymbol{d}[\unicode[STIX]{x1D6FC}]^{\times }$
of degree
$g\in \boldsymbol{d}[\unicode[STIX]{x1D6FC}]^{\times }$
of degree
![]() $u$
over
$u$
over
![]() $\boldsymbol{d}$
, where
$\boldsymbol{d}$
, where
![]() $\unicode[STIX]{x1D6FE}$
runs over
$\unicode[STIX]{x1D6FE}$
runs over
![]() $\text{Gal}(\boldsymbol{d}[\unicode[STIX]{x1D6FC}]/\boldsymbol{d})$
.
$\text{Gal}(\boldsymbol{d}[\unicode[STIX]{x1D6FC}]/\boldsymbol{d})$
.
The character
![]() $\unicode[STIX]{x1D6FC}\in \text{X}$
thus defines a supercuspidal
$\unicode[STIX]{x1D6FC}\in \text{X}$
thus defines a supercuspidal
![]() $\text{R}$
-representation
$\text{R}$
-representation
of the Levi subgroup
![]() $\text{GL}_{u}(\boldsymbol{d})\times \cdots \times \text{GL}_{u}(\boldsymbol{d})$
in
$\text{GL}_{u}(\boldsymbol{d})\times \cdots \times \text{GL}_{u}(\boldsymbol{d})$
in
![]() $\mathscr{G}$
. Moreover, the fibres of the map
$\mathscr{G}$
. Moreover, the fibres of the map
![]() $\unicode[STIX]{x1D6FC}\mapsto \boldsymbol{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D6FC})$
are the
$\unicode[STIX]{x1D6FC}\mapsto \boldsymbol{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D6FC})$
are the
![]() $\unicode[STIX]{x1D6F4}$
-orbits of
$\unicode[STIX]{x1D6F4}$
-orbits of
![]() $\text{X}$
. Write
$\text{X}$
. Write
![]() $r$
for the integer defined by
$r$
for the integer defined by
![]() $ru=m\text{sp}\prime$
. The maximal order
$ru=m\text{sp}\prime$
. The maximal order
![]() $\mathfrak{b}$
contains a unique principal order
$\mathfrak{b}$
contains a unique principal order
![]() $\mathfrak{b}_{r}$
of period
$\mathfrak{b}_{r}$
of period
![]() $r$
whose image under (3.3) consists of matrices with entries in the ring of integers of
$r$
whose image under (3.3) consists of matrices with entries in the ring of integers of
![]() $\text{D}\text{sp}\prime$
whose reduction modulo its maximal ideal is upper triangular by blocks of size
$\text{D}\text{sp}\prime$
whose reduction modulo its maximal ideal is upper triangular by blocks of size
![]() $r$
. We write
$r$
. We write
![]() $\mathfrak{a}_{r}$
for the unique order normalized by
$\mathfrak{a}_{r}$
for the unique order normalized by
![]() $\text{F}[\unicode[STIX]{x1D6FD}]^{\times }$
such that
$\text{F}[\unicode[STIX]{x1D6FD}]^{\times }$
such that
![]() $\mathfrak{a}_{r}\,\cap \,\text{B}=\mathfrak{b}_{r}$
, and
$\mathfrak{a}_{r}\,\cap \,\text{B}=\mathfrak{b}_{r}$
, and
![]() $\unicode[STIX]{x1D705}_{r}$
for the transfer of
$\unicode[STIX]{x1D705}_{r}$
for the transfer of
![]() $\unicode[STIX]{x1D705}$
with respect to the simple stratum
$\unicode[STIX]{x1D705}$
with respect to the simple stratum
![]() $[\mathfrak{a}_{r},\unicode[STIX]{x1D6FD}]$
in the sense of [Reference Mínguez and SécherreMS14b, Proposition 2.3]. Considering
$[\mathfrak{a}_{r},\unicode[STIX]{x1D6FD}]$
in the sense of [Reference Mínguez and SécherreMS14b, Proposition 2.3]. Considering
![]() $\boldsymbol{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D6FC})$
as a representation of the group
$\boldsymbol{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D6FC})$
as a representation of the group
![]() $\text{J}_{r}=\text{J}(\mathfrak{a}_{r},\unicode[STIX]{x1D6FD})$
that is trivial on
$\text{J}_{r}=\text{J}(\mathfrak{a}_{r},\unicode[STIX]{x1D6FD})$
that is trivial on
![]() $\text{J}^{1}(\mathfrak{a}_{r},\unicode[STIX]{x1D6FD})$
, we define
$\text{J}^{1}(\mathfrak{a}_{r},\unicode[STIX]{x1D6FD})$
, we define
which is a simple supertype in
![]() $\text{G}$
defined on
$\text{G}$
defined on
![]() $\text{J}_{r}$
in the sense of [Reference Sécherre and StevensSS16]. Write
$\text{J}_{r}$
in the sense of [Reference Sécherre and StevensSS16]. Write
![]() $\unicode[STIX]{x1D6E4}$
for the Galois group of
$\unicode[STIX]{x1D6E4}$
for the Galois group of
![]() $\boldsymbol{k}$
over
$\boldsymbol{k}$
over
![]() $\boldsymbol{e}$
, where
$\boldsymbol{e}$
, where
![]() $\boldsymbol{e}$
denotes the residue field of
$\boldsymbol{e}$
denotes the residue field of
![]() $\text{F}[\unicode[STIX]{x1D6FD}]$
.
$\text{F}[\unicode[STIX]{x1D6FD}]$
.
Write
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
for the endo-class of the simple character
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
for the endo-class of the simple character
![]() $\unicode[STIX]{x1D703}\in \mathscr{C}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
, and
$\unicode[STIX]{x1D703}\in \mathscr{C}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
, and
![]() $\mathscr{T}(\text{G},\boldsymbol{\unicode[STIX]{x1D6E9}},\text{R})$
for the set of isomorphism classes of simple
$\mathscr{T}(\text{G},\boldsymbol{\unicode[STIX]{x1D6E9}},\text{R})$
for the set of isomorphism classes of simple
![]() $\text{R}$
-supertypes in
$\text{R}$
-supertypes in
![]() $\text{G}$
with endo-class
$\text{G}$
with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
, that is, simple
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
, that is, simple
![]() $\text{R}$
-supertypes whose associated simple character has endo-class
$\text{R}$
-supertypes whose associated simple character has endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
.
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
.
Recall [Reference Sécherre and StevensSS16, Definition 6.1] that two simple
![]() $\text{R}$
-supertypes in
$\text{R}$
-supertypes in
![]() $\text{G}$
are said to be equivalent if the representations of
$\text{G}$
are said to be equivalent if the representations of
![]() $\text{G}$
obtained from them by compact induction are isomorphic.
$\text{G}$
obtained from them by compact induction are isomorphic.
Proposition 3.5. The map
induces a surjection from
![]() $\text{X}$
onto the set of equivalence classes of
$\text{X}$
onto the set of equivalence classes of
![]() $\mathscr{T}(\text{G},\boldsymbol{\unicode[STIX]{x1D6E9}},\text{R})$
. The fibres of this map are the
$\mathscr{T}(\text{G},\boldsymbol{\unicode[STIX]{x1D6E9}},\text{R})$
. The fibres of this map are the
![]() $\unicode[STIX]{x1D6E4}$
-orbits of
$\unicode[STIX]{x1D6E4}$
-orbits of
![]() $\text{X}$
.
$\text{X}$
.
Proof. Surjectivity follows from the definition of a simple supertype [Reference Sécherre and StevensSS16, § 2.2] and the fact that any supercuspidal irreducible
![]() $\text{R}$
-representation of
$\text{R}$
-representation of
![]() $\mathscr{G}$
is of the form
$\mathscr{G}$
is of the form
![]() $\boldsymbol{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D6FC})$
for some
$\boldsymbol{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D6FC})$
for some
![]() $\unicode[STIX]{x1D6FC}\in \text{X}$
with trivial
$\unicode[STIX]{x1D6FC}\in \text{X}$
with trivial
![]() $\unicode[STIX]{x1D6F4}$
-stabilizer.
$\unicode[STIX]{x1D6F4}$
-stabilizer.
The description of the fibres follows from [Reference Sécherre and StevensSS12, Theorem 7.2] together with the fact that the map
![]() $\unicode[STIX]{x1D6FC}\mapsto \boldsymbol{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D6FC})$
is
$\unicode[STIX]{x1D6FC}\mapsto \boldsymbol{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D6FC})$
is
![]() $\unicode[STIX]{x1D6E4}$
-equivariant, with fibres being the
$\unicode[STIX]{x1D6E4}$
-equivariant, with fibres being the
![]() $\unicode[STIX]{x1D6F4}$
-orbits of
$\unicode[STIX]{x1D6F4}$
-orbits of
![]() $\text{X}$
. Note that [Reference Sécherre and StevensSS12] is written for complex representations, but [Reference Sécherre and StevensSS12, Theorem 7.2] holds in any characteristic different from
$\text{X}$
. Note that [Reference Sécherre and StevensSS12] is written for complex representations, but [Reference Sécherre and StevensSS12, Theorem 7.2] holds in any characteristic different from
![]() $p$
.◻
$p$
.◻
Proposition 3.6. The bijection
depends only on the choice of
![]() $\unicode[STIX]{x1D705}$
, not on that of the isomorphism (3.3).
$\unicode[STIX]{x1D705}$
, not on that of the isomorphism (3.3).
Proof. Choosing another isomorphism
![]() $\text{B}\simeq \text{M}_{m\text{sp}\prime }(\text{D}\text{sp}\prime )$
such that the image of
$\text{B}\simeq \text{M}_{m\text{sp}\prime }(\text{D}\text{sp}\prime )$
such that the image of
![]() $\mathfrak{b}$
is the maximal order made of all matrices with integer entries has the effect (according to the Skolem–Noether Theorem) of conjugating by an element
$\mathfrak{b}$
is the maximal order made of all matrices with integer entries has the effect (according to the Skolem–Noether Theorem) of conjugating by an element
![]() $g\in \text{GL}_{m\text{sp}\prime }(\text{D}\text{sp}\prime )$
normalizing this standard maximal order. Thus, if
$g\in \text{GL}_{m\text{sp}\prime }(\text{D}\text{sp}\prime )$
normalizing this standard maximal order. Thus, if
![]() $\boldsymbol{\unicode[STIX]{x1D70E}}\text{sp}\prime (\unicode[STIX]{x1D6FC})$
is the representation of
$\boldsymbol{\unicode[STIX]{x1D70E}}\text{sp}\prime (\unicode[STIX]{x1D6FC})$
is the representation of
![]() $\text{J}_{r}$
trivial on
$\text{J}_{r}$
trivial on
![]() $\text{J}^{1}(\mathfrak{a}_{r},\unicode[STIX]{x1D6FD})$
corresponding to
$\text{J}^{1}(\mathfrak{a}_{r},\unicode[STIX]{x1D6FD})$
corresponding to
![]() $\unicode[STIX]{x1D6FC}$
with respect to that choice of isomorphism, it differs from
$\unicode[STIX]{x1D6FC}$
with respect to that choice of isomorphism, it differs from
![]() $\boldsymbol{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D6FC})$
by conjugation by
$\boldsymbol{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D6FC})$
by conjugation by
![]() $g$
.◻
$g$
.◻
Remark 3.7. Suppose that
![]() $\boldsymbol{k}_{1}$
is another extension of
$\boldsymbol{k}_{1}$
is another extension of
![]() $\boldsymbol{d}$
of degree
$\boldsymbol{d}$
of degree
![]() $m\text{sp}\prime$
. Write
$m\text{sp}\prime$
. Write
![]() $\text{X}_{1}$
for the group of
$\text{X}_{1}$
for the group of
![]() $\text{R}$
-characters of its invertible elements and
$\text{R}$
-characters of its invertible elements and
![]() $\unicode[STIX]{x1D6E4}_{1}$
for the Galois group
$\unicode[STIX]{x1D6E4}_{1}$
for the Galois group
![]() $\text{Gal}(\boldsymbol{k}_{1}/\boldsymbol{e})$
. Let
$\text{Gal}(\boldsymbol{k}_{1}/\boldsymbol{e})$
. Let
![]() $\mathbf{t}$
denote the bijection (3.5) and write
$\mathbf{t}$
denote the bijection (3.5) and write
![]() $\mathbf{t}_{1}$
for its analogue obtained by replacing
$\mathbf{t}_{1}$
for its analogue obtained by replacing
![]() $\boldsymbol{k}$
with
$\boldsymbol{k}$
with
![]() $\boldsymbol{k}_{1}$
. Choosing an isomorphism of
$\boldsymbol{k}_{1}$
. Choosing an isomorphism of
![]() $\boldsymbol{e}$
-algebras
$\boldsymbol{e}$
-algebras
![]() $\boldsymbol{k}\rightarrow \boldsymbol{k}_{1}$
induces a bijection
$\boldsymbol{k}\rightarrow \boldsymbol{k}_{1}$
induces a bijection
which does not depend on this choice, and one has
![]() $\mathbf{t}_{1}=\mathbf{t}\circ \mathbf{b}$
.
$\mathbf{t}_{1}=\mathbf{t}\circ \mathbf{b}$
.
3.4
Recall [Reference Mínguez and SécherreMS14b] that any supercuspidal
![]() $\text{R}$
-representation
$\text{R}$
-representation
![]() $\unicode[STIX]{x1D70C}$
of
$\unicode[STIX]{x1D70C}$
of
![]() $\text{G}$
contains a maximal simple character, uniquely determined up to
$\text{G}$
contains a maximal simple character, uniquely determined up to
![]() $\text{G}$
-conjugacy. We define the endo-class of
$\text{G}$
-conjugacy. We define the endo-class of
![]() $\unicode[STIX]{x1D70C}$
to be the endo-class of any simple character contained in
$\unicode[STIX]{x1D70C}$
to be the endo-class of any simple character contained in
![]() $\unicode[STIX]{x1D70C}$
. If we write
$\unicode[STIX]{x1D70C}$
. If we write
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
for this endo-class, then
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
for this endo-class, then
![]() $\unicode[STIX]{x1D70C}$
contains a simple
$\unicode[STIX]{x1D70C}$
contains a simple
![]() $\text{R}$
-supertype
$\text{R}$
-supertype
![]() $\boldsymbol{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})\in \mathscr{T}(\text{G},\boldsymbol{\unicode[STIX]{x1D6E9}},\text{R})$
for some
$\boldsymbol{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})\in \mathscr{T}(\text{G},\boldsymbol{\unicode[STIX]{x1D6E9}},\text{R})$
for some
![]() $\unicode[STIX]{x1D6FC}\in \text{X}$
with trivial
$\unicode[STIX]{x1D6FC}\in \text{X}$
with trivial
![]() $\unicode[STIX]{x1D6F4}$
-stabilizer.
$\unicode[STIX]{x1D6F4}$
-stabilizer.
Remark 3.8. The positive integer
![]() $s(\unicode[STIX]{x1D70C})$
associated with
$s(\unicode[STIX]{x1D70C})$
associated with
![]() $\unicode[STIX]{x1D70C}$
in § 3.1 is the order of the
$\unicode[STIX]{x1D70C}$
in § 3.1 is the order of the
![]() $\unicode[STIX]{x1D6E4}$
-stabilizer of
$\unicode[STIX]{x1D6E4}$
-stabilizer of
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.
3.5
We call an inertial class of supercuspidal pairs of
![]() $\text{G}$
simple if it contains a pair of the form
$\text{G}$
simple if it contains a pair of the form
for some integer
![]() $r$
dividing
$r$
dividing
![]() $m$
and some supercuspidal
$m$
and some supercuspidal
![]() $\text{R}$
-representation
$\text{R}$
-representation
![]() $\unicode[STIX]{x1D70C}$
of
$\unicode[STIX]{x1D70C}$
of
![]() $\text{GL}_{m/r}(\text{D})$
, and we define the endo-class of such an inertial class to be the endo-class of
$\text{GL}_{m/r}(\text{D})$
, and we define the endo-class of such an inertial class to be the endo-class of
![]() $\unicode[STIX]{x1D70C}$
, that is, the endo-class of any simple character contained in
$\unicode[STIX]{x1D70C}$
, that is, the endo-class of any simple character contained in
![]() $\unicode[STIX]{x1D70C}$
. By [Reference Sécherre and StevensSS16, § 8], there is a bijective correspondence between simple inertial classes of supercuspidal pairs of
$\unicode[STIX]{x1D70C}$
. By [Reference Sécherre and StevensSS16, § 8], there is a bijective correspondence between simple inertial classes of supercuspidal pairs of
![]() $\text{G}$
and equivalence classes of simple supertypes of
$\text{G}$
and equivalence classes of simple supertypes of
![]() $\text{G}$
, that preserves endo-classes. More precisely, the inertial class of (3.6), denoted by
$\text{G}$
, that preserves endo-classes. More precisely, the inertial class of (3.6), denoted by
![]() $\unicode[STIX]{x1D6FA}$
, corresponds to the equivalence class of a simple supertype
$\unicode[STIX]{x1D6FA}$
, corresponds to the equivalence class of a simple supertype
![]() $(\text{J},\unicode[STIX]{x1D706})$
if and only if the irreducible representations of
$(\text{J},\unicode[STIX]{x1D706})$
if and only if the irreducible representations of
![]() $\text{G}$
occurring as a subquotient of the compact induction of
$\text{G}$
occurring as a subquotient of the compact induction of
![]() $\unicode[STIX]{x1D706}$
to
$\unicode[STIX]{x1D706}$
to
![]() $\text{G}$
are exactly those irreducible representations of
$\text{G}$
are exactly those irreducible representations of
![]() $\text{G}$
occurring as a subquotient of the parabolic induction to
$\text{G}$
occurring as a subquotient of the parabolic induction to
![]() $\text{G}$
of an element of
$\text{G}$
of an element of
![]() $\unicode[STIX]{x1D6FA}$
.
$\unicode[STIX]{x1D6FA}$
.
From the previous subsection, we have an endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
and a maximal
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
and a maximal
![]() $\unicode[STIX]{x1D6FD}$
-extension
$\unicode[STIX]{x1D6FD}$
-extension
![]() $\unicode[STIX]{x1D705}$
. Combining the map (3.4) with the correspondence between simple inertial classes of supercuspidal pairs and equivalence classes of simple supertypes, we get the following result. Given
$\unicode[STIX]{x1D705}$
. Combining the map (3.4) with the correspondence between simple inertial classes of supercuspidal pairs and equivalence classes of simple supertypes, we get the following result. Given
![]() $\unicode[STIX]{x1D6FC}\in \text{X}$
, we write
$\unicode[STIX]{x1D6FC}\in \text{X}$
, we write
![]() $\boldsymbol{\unicode[STIX]{x1D6FA}}(\unicode[STIX]{x1D6FC})$
for the inertial class of supercuspidal pairs of
$\boldsymbol{\unicode[STIX]{x1D6FA}}(\unicode[STIX]{x1D6FC})$
for the inertial class of supercuspidal pairs of
![]() $\text{G}$
that corresponds to
$\text{G}$
that corresponds to
![]() $\boldsymbol{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})$
.
$\boldsymbol{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})$
.
Proposition 3.9. The map
induces a surjection from
![]() $\text{X}$
to the set of simple inertial classes of supercuspidal pairs of
$\text{X}$
to the set of simple inertial classes of supercuspidal pairs of
![]() $\text{G}$
with associated endo-class
$\text{G}$
with associated endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
. Its fibres are the
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
. Its fibres are the
![]() $\unicode[STIX]{x1D6E4}$
-orbits of
$\unicode[STIX]{x1D6E4}$
-orbits of
![]() $\text{X}$
.
$\text{X}$
.
Let us recall the following important result [Reference Mínguez and SécherreMS14a, Théorème 8.16]: given an irreducible
![]() $\text{R}$
-representation
$\text{R}$
-representation
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $\text{G}$
, there are integers
$\text{G}$
, there are integers
![]() $m_{1},\ldots ,m_{r}\geqslant 1$
such that
$m_{1},\ldots ,m_{r}\geqslant 1$
such that
![]() $m_{1}+\cdots +m_{r}=m$
and supercuspidal irreducible representations
$m_{1}+\cdots +m_{r}=m$
and supercuspidal irreducible representations
![]() $\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{r}$
of
$\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{r}$
of
![]() $\text{GL}_{m_{1}}(\text{D}),\ldots ,\text{GL}_{m_{r}}(\text{D})$
, respectively, such that
$\text{GL}_{m_{1}}(\text{D}),\ldots ,\text{GL}_{m_{r}}(\text{D})$
, respectively, such that
![]() $\unicode[STIX]{x1D70B}$
occurs as a subquotient of the induced representation
$\unicode[STIX]{x1D70B}$
occurs as a subquotient of the induced representation
![]() $\unicode[STIX]{x1D70C}_{1}\times \cdots \times \unicode[STIX]{x1D70C}_{r}$
. Moreover, up to renumbering, the supercuspidal representations
$\unicode[STIX]{x1D70C}_{1}\times \cdots \times \unicode[STIX]{x1D70C}_{r}$
. Moreover, up to renumbering, the supercuspidal representations
![]() $\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{r}$
are unique. The conjugacy class of the supercuspidal pair
$\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{r}$
are unique. The conjugacy class of the supercuspidal pair
![]() $(\text{GL}_{m_{1}}(\text{D})\times \cdots \times \text{GL}_{m_{r}}(\text{D}),\unicode[STIX]{x1D70C}_{1}\,\otimes \,\ldots \,\otimes \,\unicode[STIX]{x1D70C}_{r})$
is called the supercuspidal support of
$(\text{GL}_{m_{1}}(\text{D})\times \cdots \times \text{GL}_{m_{r}}(\text{D}),\unicode[STIX]{x1D70C}_{1}\,\otimes \,\ldots \,\otimes \,\unicode[STIX]{x1D70C}_{r})$
is called the supercuspidal support of
![]() $\unicode[STIX]{x1D70B}$
.
$\unicode[STIX]{x1D70B}$
.
Let us call an irreducible
![]() $\text{R}$
-representation of
$\text{R}$
-representation of
![]() $\text{G}$
simple if the inertial class of its supercuspidal support is simple. For instance, any discrete series
$\text{G}$
simple if the inertial class of its supercuspidal support is simple. For instance, any discrete series
![]() $\text{R}$
-representation of
$\text{R}$
-representation of
![]() $\text{G}$
is simple. We define the endo-class of a simple irreducible representation to be that of its supercuspidal support.
$\text{G}$
is simple. We define the endo-class of a simple irreducible representation to be that of its supercuspidal support.
Definition 3.10. Let
![]() $\unicode[STIX]{x1D70B}$
be a simple irreducible representation of
$\unicode[STIX]{x1D70B}$
be a simple irreducible representation of
![]() $\text{G}$
with endo-class
$\text{G}$
with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
. The parametrizing class of
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
. The parametrizing class of
![]() $\unicode[STIX]{x1D70B}$
is the
$\unicode[STIX]{x1D70B}$
is the
![]() $\unicode[STIX]{x1D6E4}$
-orbit of a character
$\unicode[STIX]{x1D6E4}$
-orbit of a character
![]() $\unicode[STIX]{x1D6FC}\in \text{X}$
such that the two following equivalent conditions hold:
$\unicode[STIX]{x1D6FC}\in \text{X}$
such that the two following equivalent conditions hold:
(1) the supercuspidal support of
 $\unicode[STIX]{x1D70B}$
belongs to the inertial class
$\unicode[STIX]{x1D70B}$
belongs to the inertial class
 $\boldsymbol{\unicode[STIX]{x1D6FA}}(\unicode[STIX]{x1D6FC})$
;
$\boldsymbol{\unicode[STIX]{x1D6FA}}(\unicode[STIX]{x1D6FC})$
;(2) the representation
 $\unicode[STIX]{x1D70B}$
occurs as a subquotient of the compact induction of
$\unicode[STIX]{x1D70B}$
occurs as a subquotient of the compact induction of
 $\boldsymbol{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})$
to
$\boldsymbol{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})$
to
 $\text{G}$
.
$\text{G}$
.
The parametrizing class of
![]() $\unicode[STIX]{x1D70B}$
is denoted by
$\unicode[STIX]{x1D70B}$
is denoted by
![]() $\text{X}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D70B})$
, or simply
$\text{X}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D70B})$
, or simply
![]() $\text{X}(\unicode[STIX]{x1D70B})$
if there is no ambiguity as to the maximal
$\text{X}(\unicode[STIX]{x1D70B})$
if there is no ambiguity as to the maximal
![]() $\unicode[STIX]{x1D6FD}$
-extension
$\unicode[STIX]{x1D6FD}$
-extension
![]() $\unicode[STIX]{x1D705}$
.
$\unicode[STIX]{x1D705}$
.
Remark 3.11. Let
![]() $\unicode[STIX]{x1D705}\text{sp}\prime$
be another maximal
$\unicode[STIX]{x1D705}\text{sp}\prime$
be another maximal
![]() $\unicode[STIX]{x1D6FD}$
-extension of the simple character
$\unicode[STIX]{x1D6FD}$
-extension of the simple character
![]() $\unicode[STIX]{x1D703}\in \mathscr{C}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
in
$\unicode[STIX]{x1D703}\in \mathscr{C}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
in
![]() $\text{G}$
. By [Reference SécherreSéc05a, Théorème 2.28] there is a character
$\text{G}$
. By [Reference SécherreSéc05a, Théorème 2.28] there is a character
![]() $\unicode[STIX]{x1D712}$
of
$\unicode[STIX]{x1D712}$
of
![]() $\boldsymbol{e}^{\times }$
such that
$\boldsymbol{e}^{\times }$
such that
![]() $\unicode[STIX]{x1D705}\text{sp}\prime =\unicode[STIX]{x1D705}\unicode[STIX]{x1D701}$
, where
$\unicode[STIX]{x1D705}\text{sp}\prime =\unicode[STIX]{x1D705}\unicode[STIX]{x1D701}$
, where
![]() $\unicode[STIX]{x1D701}$
is the character of
$\unicode[STIX]{x1D701}$
is the character of
![]() $\text{J}$
trivial on
$\text{J}$
trivial on
![]() $\text{J}^{1}$
that corresponds to the character
$\text{J}^{1}$
that corresponds to the character
![]() $\unicode[STIX]{x1D712}\circ \text{N}_{\boldsymbol{d}/\boldsymbol{e}}\circ \det$
of
$\unicode[STIX]{x1D712}\circ \text{N}_{\boldsymbol{d}/\boldsymbol{e}}\circ \det$
of
![]() $\mathscr{G}$
, where
$\mathscr{G}$
, where
![]() $\text{N}_{\boldsymbol{d}/\boldsymbol{e}}$
is the norm map with respect to
$\text{N}_{\boldsymbol{d}/\boldsymbol{e}}$
is the norm map with respect to
![]() $\boldsymbol{d}/\boldsymbol{e}$
. Then we have
$\boldsymbol{d}/\boldsymbol{e}$
. Then we have
![]() $\unicode[STIX]{x1D6FC}\text{sp}\prime \in \text{X}(\unicode[STIX]{x1D705}\text{sp}\prime ,\unicode[STIX]{x1D70B})$
if and only if
$\unicode[STIX]{x1D6FC}\text{sp}\prime \in \text{X}(\unicode[STIX]{x1D705}\text{sp}\prime ,\unicode[STIX]{x1D70B})$
if and only if
![]() $\unicode[STIX]{x1D6FC}\text{sp}\prime \unicode[STIX]{x1D707}\in \text{X}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D70B})$
, where
$\unicode[STIX]{x1D6FC}\text{sp}\prime \unicode[STIX]{x1D707}\in \text{X}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D70B})$
, where
![]() $\unicode[STIX]{x1D707}$
is the character
$\unicode[STIX]{x1D707}$
is the character
![]() $\unicode[STIX]{x1D712}\circ \text{N}_{\boldsymbol{k}/\boldsymbol{e}}$
of
$\unicode[STIX]{x1D712}\circ \text{N}_{\boldsymbol{k}/\boldsymbol{e}}$
of
![]() $\boldsymbol{k}^{\times }$
.
$\boldsymbol{k}^{\times }$
.
Remark 3.12. When
![]() $\text{R}$
has characteristic
$\text{R}$
has characteristic
![]() $0$
, the two equivalent conditions of Definition 3.10 are also equivalent to:
$0$
, the two equivalent conditions of Definition 3.10 are also equivalent to:
(3) the representation
 $\unicode[STIX]{x1D70B}$
occurs as a quotient of the compact induction of
$\unicode[STIX]{x1D70B}$
occurs as a quotient of the compact induction of
 $\boldsymbol{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})$
to
$\boldsymbol{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})$
to
 $\text{G}$
.
$\text{G}$
.
Equivalently, the restriction of
![]() $\unicode[STIX]{x1D70B}$
to
$\unicode[STIX]{x1D70B}$
to
![]() $\text{J}_{r}$
contains
$\text{J}_{r}$
contains
![]() $\boldsymbol{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})$
as a subrepresentation.
$\boldsymbol{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})$
as a subrepresentation.
4 Linked
 $\ell$
-adic representations
$\ell$
-adic representations
In this section, we fix a prime number
![]() $\ell$
different from
$\ell$
different from
![]() $p$
. We will distinguish between
$p$
. We will distinguish between
![]() $\ell$
-adic and mod
$\ell$
-adic and mod
![]() $\ell$
representations by using a tilde
$\ell$
representations by using a tilde
![]() $\widetilde{\phantom{\unicode[STIX]{x1D70B}}}$
for
$\widetilde{\phantom{\unicode[STIX]{x1D70B}}}$
for
![]() $\ell$
-adic representations.
$\ell$
-adic representations.
4.1
Let
![]() $\widetilde{\unicode[STIX]{x1D70B}}$
be an irreducible
$\widetilde{\unicode[STIX]{x1D70B}}$
be an irreducible
![]() $\ell$
-adic representation of
$\ell$
-adic representation of
![]() $\text{G}$
. Fix a representative
$\text{G}$
. Fix a representative
![]() $(\text{M},\widetilde{\unicode[STIX]{x1D70C}})$
in the inertial class of its cuspidal support, with
$(\text{M},\widetilde{\unicode[STIX]{x1D70C}})$
in the inertial class of its cuspidal support, with
![]() $\text{M}$
a standard Levi subgroup
$\text{M}$
a standard Levi subgroup
![]() $\text{GL}_{m_{1}}(\text{D})\times \cdots \times \text{GL}_{m_{r}}(\text{D})$
and
$\text{GL}_{m_{1}}(\text{D})\times \cdots \times \text{GL}_{m_{r}}(\text{D})$
and
![]() $\widetilde{\unicode[STIX]{x1D70C}}$
of the form
$\widetilde{\unicode[STIX]{x1D70C}}$
of the form
![]() $\widetilde{\unicode[STIX]{x1D70C}}_{1}\otimes \cdots \otimes \widetilde{\unicode[STIX]{x1D70C}}_{r}$
where
$\widetilde{\unicode[STIX]{x1D70C}}_{1}\otimes \cdots \otimes \widetilde{\unicode[STIX]{x1D70C}}_{r}$
where
![]() $\widetilde{\unicode[STIX]{x1D70C}}_{i}$
is an
$\widetilde{\unicode[STIX]{x1D70C}}_{i}$
is an
![]() $\ell$
-adic cuspidal irreducible representation of
$\ell$
-adic cuspidal irreducible representation of
![]() $\text{GL}_{m_{i}}(\text{D})$
for
$\text{GL}_{m_{i}}(\text{D})$
for
![]() $i\in \{1,\ldots ,r\}$
, and with
$i\in \{1,\ldots ,r\}$
, and with
![]() $m_{1}+\cdots +m_{r}=m$
. Since
$m_{1}+\cdots +m_{r}=m$
. Since
![]() $\widetilde{\unicode[STIX]{x1D70C}}_{i}$
is determined up to an unramified twist, we may assume that it is integral (see § 3.2) and fix an irreducible subquotient
$\widetilde{\unicode[STIX]{x1D70C}}_{i}$
is determined up to an unramified twist, we may assume that it is integral (see § 3.2) and fix an irreducible subquotient
![]() $\unicode[STIX]{x1D70C}_{i}$
of its reduction mod
$\unicode[STIX]{x1D70C}_{i}$
of its reduction mod
![]() $\ell$
. By the classification of mod
$\ell$
. By the classification of mod
![]() $\ell$
irreducible cuspidal representations in terms of supercuspidal representations [Reference Mínguez and SécherreMS14a, Théorème 6.14], there are a unique integer
$\ell$
irreducible cuspidal representations in terms of supercuspidal representations [Reference Mínguez and SécherreMS14a, Théorème 6.14], there are a unique integer
![]() $u_{i}\geqslant 1$
dividing
$u_{i}\geqslant 1$
dividing
![]() $m_{i}$
and a supercuspidal irreducible representation
$m_{i}$
and a supercuspidal irreducible representation
![]() $\unicode[STIX]{x1D70F}_{i}$
of degree
$\unicode[STIX]{x1D70F}_{i}$
of degree
![]() $u_{i}$
such that the supercuspidal support of
$u_{i}$
such that the supercuspidal support of
![]() $\unicode[STIX]{x1D70C}_{i}$
is inertially equivalent to
$\unicode[STIX]{x1D70C}_{i}$
is inertially equivalent to
where the factors are repeated
![]() $k_{i}$
times, with
$k_{i}$
times, with
![]() $m_{i}=k_{i}u_{i}$
.
$m_{i}=k_{i}u_{i}$
.
Definition 4.1. Let
![]() $\widetilde{\unicode[STIX]{x1D70B}}$
be an irreducible
$\widetilde{\unicode[STIX]{x1D70B}}$
be an irreducible
![]() $\ell$
-adic representation of
$\ell$
-adic representation of
![]() $\text{G}$
as above. Let us write
$\text{G}$
as above. Let us write
The inertial class in
![]() $\text{G}$
of the supercuspidal pair
$\text{G}$
of the supercuspidal pair
![]() $(\text{L},\unicode[STIX]{x1D70F})$
, denoted by
$(\text{L},\unicode[STIX]{x1D70F})$
, denoted by
![]() $\text{}\text{i}_{\ell }(\widetilde{\unicode[STIX]{x1D70B}})$
, is uniquely determined by the irreducible representation
$\text{}\text{i}_{\ell }(\widetilde{\unicode[STIX]{x1D70B}})$
, is uniquely determined by the irreducible representation
![]() $\widetilde{\unicode[STIX]{x1D70B}}$
. It is called the mod-
$\widetilde{\unicode[STIX]{x1D70B}}$
. It is called the mod-
![]() $\ell$
inertial supercuspidal support of
$\ell$
inertial supercuspidal support of
![]() $\widetilde{\unicode[STIX]{x1D70B}}$
.
$\widetilde{\unicode[STIX]{x1D70B}}$
.
Definition 4.2. Two irreducible
![]() $\ell$
-adic representations
$\ell$
-adic representations
![]() $\widetilde{\unicode[STIX]{x1D70B}}_{1}$
and
$\widetilde{\unicode[STIX]{x1D70B}}_{1}$
and
![]() $\widetilde{\unicode[STIX]{x1D70B}}_{2}$
of
$\widetilde{\unicode[STIX]{x1D70B}}_{2}$
of
![]() $\text{G}$
are said to belong to the same
$\text{G}$
are said to belong to the same
![]() $\ell$
-block if
$\ell$
-block if
![]() $\text{}\text{i}_{\ell }(\widetilde{\unicode[STIX]{x1D70B}}_{1})=\text{}\text{i}_{\ell }(\widetilde{\unicode[STIX]{x1D70B}}_{2})$
.
$\text{}\text{i}_{\ell }(\widetilde{\unicode[STIX]{x1D70B}}_{1})=\text{}\text{i}_{\ell }(\widetilde{\unicode[STIX]{x1D70B}}_{2})$
.
An
![]() $\ell$
-block in the set
$\ell$
-block in the set
![]() $\text{Irr}(\text{G},\overline{\mathbf{Q}}_{\ell })$
of all isomorphism classes of irreducible
$\text{Irr}(\text{G},\overline{\mathbf{Q}}_{\ell })$
of all isomorphism classes of irreducible
![]() $\ell$
-adic representations of
$\ell$
-adic representations of
![]() $\text{G}$
is an equivalence class for the equivalence relation defined by
$\text{G}$
is an equivalence class for the equivalence relation defined by
![]() $\text{}\text{i}_{\ell }$
.
$\text{}\text{i}_{\ell }$
.
Let
![]() $\widetilde{\unicode[STIX]{x1D70B}}$
be an irreducible
$\widetilde{\unicode[STIX]{x1D70B}}$
be an irreducible
![]() $\ell$
-adic representation of
$\ell$
-adic representation of
![]() $\text{G}$
as above. By definition,
$\text{G}$
as above. By definition,
![]() $\text{}\text{i}_{\ell }(\widetilde{\unicode[STIX]{x1D70B}})$
depends only on the inertial class of the supercuspidal support of
$\text{}\text{i}_{\ell }(\widetilde{\unicode[STIX]{x1D70B}})$
depends only on the inertial class of the supercuspidal support of
![]() $\widetilde{\unicode[STIX]{x1D70B}}$
. Assume that
$\widetilde{\unicode[STIX]{x1D70B}}$
. Assume that
![]() $\widetilde{\unicode[STIX]{x1D70B}}$
is integral.
$\widetilde{\unicode[STIX]{x1D70B}}$
is integral.
Lemma 4.3. All irreducible subquotients occurring in
![]() $\text{}\text{r}_{\ell }(\widetilde{\unicode[STIX]{x1D70B}})$
, the reduction mod
$\text{}\text{r}_{\ell }(\widetilde{\unicode[STIX]{x1D70B}})$
, the reduction mod
![]() $\ell$
of
$\ell$
of
![]() $\widetilde{\unicode[STIX]{x1D70B}}$
, have their supercuspidal support in
$\widetilde{\unicode[STIX]{x1D70B}}$
, have their supercuspidal support in
![]() $\text{}\text{i}_{\ell }(\widetilde{\unicode[STIX]{x1D70B}})$
.
$\text{}\text{i}_{\ell }(\widetilde{\unicode[STIX]{x1D70B}})$
.
Proof. The representation
![]() $\widetilde{\unicode[STIX]{x1D70B}}$
is a subquotient of
$\widetilde{\unicode[STIX]{x1D70B}}$
is a subquotient of
![]() $\widetilde{\unicode[STIX]{x1D70C}}_{1}\times \cdots \times \widetilde{\unicode[STIX]{x1D70C}}_{r}$
. Since
$\widetilde{\unicode[STIX]{x1D70C}}_{1}\times \cdots \times \widetilde{\unicode[STIX]{x1D70C}}_{r}$
. Since
![]() $\widetilde{\unicode[STIX]{x1D70B}}$
is integral, all the
$\widetilde{\unicode[STIX]{x1D70B}}$
is integral, all the
![]() $\widetilde{\unicode[STIX]{x1D70C}}_{i}$
are integral and, by Proposition 3.2, for each
$\widetilde{\unicode[STIX]{x1D70C}}_{i}$
are integral and, by Proposition 3.2, for each
![]() $i$
there is an integer
$i$
there is an integer
![]() $a_{i}\geqslant 1$
such that
$a_{i}\geqslant 1$
such that
where
![]() $\unicode[STIX]{x1D708}$
denotes the unramified mod-
$\unicode[STIX]{x1D708}$
denotes the unramified mod-
![]() $\ell$
character ‘absolute value of the reduced norm’. Thus any irreducible subquotient of
$\ell$
character ‘absolute value of the reduced norm’. Thus any irreducible subquotient of
![]() $\text{}\text{r}_{\ell }(\widetilde{\unicode[STIX]{x1D70B}})$
occurs as a subquotient of
$\text{}\text{r}_{\ell }(\widetilde{\unicode[STIX]{x1D70B}})$
occurs as a subquotient of
![]() $\unicode[STIX]{x1D70C}_{1}\unicode[STIX]{x1D708}^{i_{1}}\times \cdots \times \unicode[STIX]{x1D70C}_{r}\unicode[STIX]{x1D708}^{i_{r}}$
for some integers
$\unicode[STIX]{x1D70C}_{1}\unicode[STIX]{x1D708}^{i_{1}}\times \cdots \times \unicode[STIX]{x1D70C}_{r}\unicode[STIX]{x1D708}^{i_{r}}$
for some integers
![]() $i_{1},\ldots ,i_{r}\in \mathbf{N}$
. The result now follows by looking at the supercuspidal support of each
$i_{1},\ldots ,i_{r}\in \mathbf{N}$
. The result now follows by looking at the supercuspidal support of each
![]() $\unicode[STIX]{x1D70C}_{i}$
.◻
$\unicode[STIX]{x1D70C}_{i}$
.◻
Corollary 4.4. Any two integral irreducible
![]() $\ell$
-adic representations of
$\ell$
-adic representations of
![]() $\text{G}$
whose reductions
$\text{G}$
whose reductions
![]() $\text{mod}\,\ell$
share a common irreducible component belong to the same
$\text{mod}\,\ell$
share a common irreducible component belong to the same
![]() $\ell$
-block.
$\ell$
-block.
4.2
Let
![]() $\widetilde{\unicode[STIX]{x1D70B}}$
be a simple irreducible
$\widetilde{\unicode[STIX]{x1D70B}}$
be a simple irreducible
![]() $\ell$
-adic representation of
$\ell$
-adic representation of
![]() $\text{G}$
. There are an integer
$\text{G}$
. There are an integer
![]() $r\geqslant 1$
dividing
$r\geqslant 1$
dividing
![]() $m$
and a cuspidal irreducible representation
$m$
and a cuspidal irreducible representation
![]() $\widetilde{\unicode[STIX]{x1D70C}}$
of
$\widetilde{\unicode[STIX]{x1D70C}}$
of
![]() $\text{G}_{m/r}$
such that the inertial class of its cuspidal support contains
$\text{G}_{m/r}$
such that the inertial class of its cuspidal support contains
We may assume that
![]() $\widetilde{\unicode[STIX]{x1D70C}}$
is integral. We fix an irreducible subquotient
$\widetilde{\unicode[STIX]{x1D70C}}$
is integral. We fix an irreducible subquotient
![]() $\unicode[STIX]{x1D70C}$
of its reduction modulo
$\unicode[STIX]{x1D70C}$
of its reduction modulo
![]() $\ell$
. As in § 4.1, there are a unique integer
$\ell$
. As in § 4.1, there are a unique integer
![]() $u\geqslant 1$
dividing
$u\geqslant 1$
dividing
![]() $m/r$
and a supercuspidal irreducible representation
$m/r$
and a supercuspidal irreducible representation
![]() $\unicode[STIX]{x1D70F}$
of degree
$\unicode[STIX]{x1D70F}$
of degree
![]() $u$
such that the supercuspidal support of
$u$
such that the supercuspidal support of
![]() $\unicode[STIX]{x1D70C}$
is inertially equivalent to
$\unicode[STIX]{x1D70C}$
is inertially equivalent to
![]() $(\text{GL}_{u}(\text{D})\times \cdots \times \text{GL}_{u}(\text{D}),\unicode[STIX]{x1D70F}\otimes \cdots \otimes \unicode[STIX]{x1D70F})$
, with
$(\text{GL}_{u}(\text{D})\times \cdots \times \text{GL}_{u}(\text{D}),\unicode[STIX]{x1D70F}\otimes \cdots \otimes \unicode[STIX]{x1D70F})$
, with
![]() $m=kur$
. Therefore, the mod-
$m=kur$
. Therefore, the mod-
![]() $\ell$
inertial supercuspidal support
$\ell$
inertial supercuspidal support
![]() $\text{}\text{i}_{\ell }(\widetilde{\unicode[STIX]{x1D70B}})$
of the
$\text{}\text{i}_{\ell }(\widetilde{\unicode[STIX]{x1D70B}})$
of the
![]() $\ell$
-adic simple irreducible representation
$\ell$
-adic simple irreducible representation
![]() $\widetilde{\unicode[STIX]{x1D70B}}$
is the inertial class of the pair
$\widetilde{\unicode[STIX]{x1D70B}}$
is the inertial class of the pair
In particular, it is simple.
Recall that, according to [Reference Mínguez and SécherreMS14a, Théorème 6.11], any supercuspidal irreducible mod-
![]() $\ell$
representation can be lifted to an
$\ell$
representation can be lifted to an
![]() $\ell$
-adic irreducible representation. The following lemma is an immediate consequence of the definition of the mod-
$\ell$
-adic irreducible representation. The following lemma is an immediate consequence of the definition of the mod-
![]() $\ell$
inertial supercuspidal support.
$\ell$
inertial supercuspidal support.
Lemma 4.5. Let
![]() $\widetilde{\unicode[STIX]{x1D70F}}$
be an
$\widetilde{\unicode[STIX]{x1D70F}}$
be an
![]() $\ell$
-adic lift of
$\ell$
-adic lift of
![]() $\unicode[STIX]{x1D70F}$
. Any simple irreducible
$\unicode[STIX]{x1D70F}$
. Any simple irreducible
![]() $\ell$
-adic representation whose cuspidal support is inertially equivalent to
$\ell$
-adic representation whose cuspidal support is inertially equivalent to
is in the same
![]() $\ell$
-block as
$\ell$
-block as
![]() $\widetilde{\unicode[STIX]{x1D70B}}$
. In particular, the
$\widetilde{\unicode[STIX]{x1D70B}}$
. In particular, the
![]() $\ell$
-adic discrete series representation
$\ell$
-adic discrete series representation
![]() $\text{L}(\widetilde{\unicode[STIX]{x1D70F}},kr)$
is in the same
$\text{L}(\widetilde{\unicode[STIX]{x1D70F}},kr)$
is in the same
![]() $\ell$
-block as
$\ell$
-block as
![]() $\widetilde{\unicode[STIX]{x1D70B}}$
.
$\widetilde{\unicode[STIX]{x1D70B}}$
.
4.3
Recall that we have fixed in § 2 a smooth character
![]() $\unicode[STIX]{x1D713}_{\ell }^{}:\text{F}\rightarrow \overline{\mathbf{Q}}_{\ell }^{\times }$
that is trivial on
$\unicode[STIX]{x1D713}_{\ell }^{}:\text{F}\rightarrow \overline{\mathbf{Q}}_{\ell }^{\times }$
that is trivial on
![]() $\mathfrak{p}$
but not on
$\mathfrak{p}$
but not on
![]() $\mathscr{O}$
. Since
$\mathscr{O}$
. Since
![]() $\text{F}$
is the union of the
$\text{F}$
is the union of the
![]() $\mathfrak{p}^{-i}$
for
$\mathfrak{p}^{-i}$
for
![]() $i\geqslant 1$
and
$i\geqslant 1$
and
![]() $p$
is invertible in
$p$
is invertible in
![]() $\overline{\mathbf{Z}}_{\ell }$
, it has values in
$\overline{\mathbf{Z}}_{\ell }$
, it has values in
![]() $\overline{\mathbf{Z}}_{\ell }^{\times }$
. For any simple stratum
$\overline{\mathbf{Z}}_{\ell }^{\times }$
. For any simple stratum
![]() $[\mathfrak{a},\unicode[STIX]{x1D6FD}]$
in
$[\mathfrak{a},\unicode[STIX]{x1D6FD}]$
in
![]() $\text{M}_{m}(\text{D})$
, the set of simple
$\text{M}_{m}(\text{D})$
, the set of simple
![]() $\ell$
-adic characters associated with
$\ell$
-adic characters associated with
![]() $[\mathfrak{a},\unicode[STIX]{x1D6FD}]$
will be defined with respect to
$[\mathfrak{a},\unicode[STIX]{x1D6FD}]$
will be defined with respect to
![]() $\unicode[STIX]{x1D713}_{\ell }$
(see § 3.3), whereas the set of
$\unicode[STIX]{x1D713}_{\ell }$
(see § 3.3), whereas the set of
![]() $\ell$
-modular simple characters associated with
$\ell$
-modular simple characters associated with
![]() $[\mathfrak{a},\unicode[STIX]{x1D6FD}]$
will be defined with respect to the reduction mod
$[\mathfrak{a},\unicode[STIX]{x1D6FD}]$
will be defined with respect to the reduction mod
![]() $\ell$
of
$\ell$
of
![]() $\unicode[STIX]{x1D713}_{\ell }^{}$
. Reduction mod
$\unicode[STIX]{x1D713}_{\ell }^{}$
. Reduction mod
![]() $\ell$
thus induces a bijection between
$\ell$
thus induces a bijection between
![]() $\ell$
-adic and
$\ell$
-adic and
![]() $\ell$
-modular simple characters associated with
$\ell$
-modular simple characters associated with
![]() $[\mathfrak{a},\unicode[STIX]{x1D6FD}]$
. It also induces a bijection between endo-classes of
$[\mathfrak{a},\unicode[STIX]{x1D6FD}]$
. It also induces a bijection between endo-classes of
![]() $\ell$
-adic and
$\ell$
-adic and
![]() $\ell$
-modular simple characters. Thus we will speak of endo-classes of simple characters, without referring to the coefficient field.
$\ell$
-modular simple characters. Thus we will speak of endo-classes of simple characters, without referring to the coefficient field.
Let
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
be the endo-class of §§ 3.3–3.5. Fix a
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
be the endo-class of §§ 3.3–3.5. Fix a
![]() $\unicode[STIX]{x1D6FD}$
-extension
$\unicode[STIX]{x1D6FD}$
-extension
![]() $\widetilde{\unicode[STIX]{x1D705}}$
of a maximal
$\widetilde{\unicode[STIX]{x1D705}}$
of a maximal
![]() $\ell$
-adic simple character in
$\ell$
-adic simple character in
![]() $\text{G}$
of endo-class
$\text{G}$
of endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
, and write
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
, and write
![]() $\text{X}_{\ell }$
for the group of
$\text{X}_{\ell }$
for the group of
![]() $\ell$
-adic characters of
$\ell$
-adic characters of
![]() $\boldsymbol{k}^{\times }$
. The map (3.4) gives us a bijection
$\boldsymbol{k}^{\times }$
. The map (3.4) gives us a bijection
![]() $\widetilde{\boldsymbol{\unicode[STIX]{x1D706}}}_{\ell }$
from
$\widetilde{\boldsymbol{\unicode[STIX]{x1D706}}}_{\ell }$
from
![]() $\text{X}_{\ell }/\unicode[STIX]{x1D6E4}$
onto the set of equivalence classes of
$\text{X}_{\ell }/\unicode[STIX]{x1D6E4}$
onto the set of equivalence classes of
![]() $\mathscr{T}(\text{G},\boldsymbol{\unicode[STIX]{x1D6E9}},\overline{\mathbf{Q}}_{\ell })$
. Also write
$\mathscr{T}(\text{G},\boldsymbol{\unicode[STIX]{x1D6E9}},\overline{\mathbf{Q}}_{\ell })$
. Also write
![]() $\text{Y}_{\ell }$
for the group of
$\text{Y}_{\ell }$
for the group of
![]() $\ell$
-modular characters of
$\ell$
-modular characters of
![]() $\boldsymbol{k}^{\times }$
, and
$\boldsymbol{k}^{\times }$
, and
![]() $\unicode[STIX]{x1D705}$
for the reduction mod
$\unicode[STIX]{x1D705}$
for the reduction mod
![]() $\ell$
of
$\ell$
of
![]() $\widetilde{\unicode[STIX]{x1D705}}$
. This gives us a bijection
$\widetilde{\unicode[STIX]{x1D705}}$
. This gives us a bijection
![]() $\boldsymbol{\unicode[STIX]{x1D706}}_{\ell }$
from
$\boldsymbol{\unicode[STIX]{x1D706}}_{\ell }$
from
![]() $\text{Y}_{\ell }/\unicode[STIX]{x1D6E4}$
onto the set of equivalence classes of
$\text{Y}_{\ell }/\unicode[STIX]{x1D6E4}$
onto the set of equivalence classes of
![]() $\mathscr{T}(\text{G},\boldsymbol{\unicode[STIX]{x1D6E9}},\overline{\mathbf{F}}_{\ell })$
. These two bijections are compatible in the following sense.
$\mathscr{T}(\text{G},\boldsymbol{\unicode[STIX]{x1D6E9}},\overline{\mathbf{F}}_{\ell })$
. These two bijections are compatible in the following sense.
Proposition 4.6. Let
![]() $\widetilde{\unicode[STIX]{x1D70B}}$
be a simple irreducible
$\widetilde{\unicode[STIX]{x1D70B}}$
be a simple irreducible
![]() $\ell$
-adic representation of
$\ell$
-adic representation of
![]() $\text{G}$
with endo-class
$\text{G}$
with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
, let
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
, let
![]() $\unicode[STIX]{x1D6FC}\in \text{X}_{\ell }(\widetilde{\unicode[STIX]{x1D70B}})$
and let
$\unicode[STIX]{x1D6FC}\in \text{X}_{\ell }(\widetilde{\unicode[STIX]{x1D70B}})$
and let
![]() $\unicode[STIX]{x1D719}\in \text{Y}_{\ell }$
be the reduction mod
$\unicode[STIX]{x1D719}\in \text{Y}_{\ell }$
be the reduction mod
![]() $\ell$
of
$\ell$
of
![]() $\unicode[STIX]{x1D6FC}$
. Then the inertial class
$\unicode[STIX]{x1D6FC}$
. Then the inertial class
![]() $\text{}\text{i}_{\ell }(\widetilde{\unicode[STIX]{x1D70B}})$
corresponds through (3.5) and (3.7) to the equivalence class of the simple supertype
$\text{}\text{i}_{\ell }(\widetilde{\unicode[STIX]{x1D70B}})$
corresponds through (3.5) and (3.7) to the equivalence class of the simple supertype
![]() $\boldsymbol{\unicode[STIX]{x1D706}}_{\ell }(\unicode[STIX]{x1D719})$
.
$\boldsymbol{\unicode[STIX]{x1D706}}_{\ell }(\unicode[STIX]{x1D719})$
.
Proof. Write the inertial class of the cuspidal support of
![]() $\widetilde{\unicode[STIX]{x1D70B}}$
as in (4.1). Let
$\widetilde{\unicode[STIX]{x1D70B}}$
as in (4.1). Let
![]() $r$
be the degree of
$r$
be the degree of
![]() $\boldsymbol{k}$
over
$\boldsymbol{k}$
over
![]() $\boldsymbol{d}[\unicode[STIX]{x1D6FC}]$
and
$\boldsymbol{d}[\unicode[STIX]{x1D6FC}]$
and
![]() $\widetilde{\unicode[STIX]{x1D70E}}_{0}$
the
$\widetilde{\unicode[STIX]{x1D70E}}_{0}$
the
![]() $\ell$
-adic supercuspidal representation of
$\ell$
-adic supercuspidal representation of
![]() $\text{GL}_{u}(\boldsymbol{k})$
associated to
$\text{GL}_{u}(\boldsymbol{k})$
associated to
![]() $\unicode[STIX]{x1D6FC}$
, where
$\unicode[STIX]{x1D6FC}$
, where
![]() $m\text{sp}\prime =ru$
. There is a maximal
$m\text{sp}\prime =ru$
. There is a maximal
![]() $\unicode[STIX]{x1D6FD}$
-extension
$\unicode[STIX]{x1D6FD}$
-extension
![]() $\widetilde{\unicode[STIX]{x1D705}}_{0}$
of
$\widetilde{\unicode[STIX]{x1D705}}_{0}$
of
![]() $\text{GL}_{m/r}(\text{D})$
such that
$\text{GL}_{m/r}(\text{D})$
such that
![]() $\widetilde{\unicode[STIX]{x1D705}}_{0}\,\otimes \,\widetilde{\unicode[STIX]{x1D70E}}_{0}$
is a maximal simple type contained in
$\widetilde{\unicode[STIX]{x1D705}}_{0}\,\otimes \,\widetilde{\unicode[STIX]{x1D70E}}_{0}$
is a maximal simple type contained in
![]() $\widetilde{\unicode[STIX]{x1D70C}}$
. More precisely, with the notation of § 3.3 and writing
$\widetilde{\unicode[STIX]{x1D70C}}$
. More precisely, with the notation of § 3.3 and writing
![]() $\text{M}_{r}$
for the Levi subgroup
$\text{M}_{r}$
for the Levi subgroup
![]() $\text{GL}_{m/r}(\text{D})\times \cdots \times \text{GL}_{m/r}(\text{D})\subseteq \text{G}$
and
$\text{GL}_{m/r}(\text{D})\times \cdots \times \text{GL}_{m/r}(\text{D})\subseteq \text{G}$
and
![]() $\text{U}_{r}$
for the unipotent radical of the parabolic subgroup comprising upper
$\text{U}_{r}$
for the unipotent radical of the parabolic subgroup comprising upper
![]() $r\times r$
block triangular matrices of
$r\times r$
block triangular matrices of
![]() $\text{G}$
, the representation of
$\text{G}$
, the representation of
![]() $\text{J}_{r}\,\cap \,\text{M}_{r}$
on the
$\text{J}_{r}\,\cap \,\text{M}_{r}$
on the
![]() $\text{J}_{r}\,\cap \,\text{U}_{r}$
-invariant subspace of
$\text{J}_{r}\,\cap \,\text{U}_{r}$
-invariant subspace of
![]() $\widetilde{\unicode[STIX]{x1D705}}_{r}$
is
$\widetilde{\unicode[STIX]{x1D705}}_{r}$
is
![]() $\widetilde{\unicode[STIX]{x1D705}}_{0}\otimes \cdots \otimes \widetilde{\unicode[STIX]{x1D705}}_{0}$
.
$\widetilde{\unicode[STIX]{x1D705}}_{0}\otimes \cdots \otimes \widetilde{\unicode[STIX]{x1D705}}_{0}$
.
Let
![]() $\unicode[STIX]{x1D70C}$
be an irreducible component of the reduction mod
$\unicode[STIX]{x1D70C}$
be an irreducible component of the reduction mod
![]() $\ell$
of
$\ell$
of
![]() $\widetilde{\unicode[STIX]{x1D70C}}$
. Then
$\widetilde{\unicode[STIX]{x1D70C}}$
. Then
![]() $\unicode[STIX]{x1D70C}$
contains the maximal simple type
$\unicode[STIX]{x1D70C}$
contains the maximal simple type
![]() $\unicode[STIX]{x1D705}_{0}\,\otimes \,\unicode[STIX]{x1D70E}_{0}$
, where
$\unicode[STIX]{x1D705}_{0}\,\otimes \,\unicode[STIX]{x1D70E}_{0}$
, where
![]() $\unicode[STIX]{x1D705}_{0}$
is the reduction mod
$\unicode[STIX]{x1D705}_{0}$
is the reduction mod
![]() $\ell$
of
$\ell$
of
![]() $\widetilde{\unicode[STIX]{x1D705}}_{0}$
and
$\widetilde{\unicode[STIX]{x1D705}}_{0}$
and
![]() $\unicode[STIX]{x1D70E}_{0}$
is that of
$\unicode[STIX]{x1D70E}_{0}$
is that of
![]() $\widetilde{\unicode[STIX]{x1D70E}}_{0}$
.
$\widetilde{\unicode[STIX]{x1D70E}}_{0}$
.
Let
![]() $t$
be the degree of
$t$
be the degree of
![]() $\boldsymbol{k}$
over
$\boldsymbol{k}$
over
![]() $\boldsymbol{d}[\unicode[STIX]{x1D719}]$
. By [Reference Mínguez and SécherreMS17, Lemme 3.2], if we write
$\boldsymbol{d}[\unicode[STIX]{x1D719}]$
. By [Reference Mínguez and SécherreMS17, Lemme 3.2], if we write
![]() $\unicode[STIX]{x1D70C}$
in the form
$\unicode[STIX]{x1D70C}$
in the form
![]() $\text{Sp}(\unicode[STIX]{x1D70F},k)$
with
$\text{Sp}(\unicode[STIX]{x1D70F},k)$
with
![]() $\unicode[STIX]{x1D70F}$
supercuspidal (see Proposition 3.1), then
$\unicode[STIX]{x1D70F}$
supercuspidal (see Proposition 3.1), then
![]() $kr=t$
and
$kr=t$
and
![]() $\unicode[STIX]{x1D70E}_{0}$
is the unique nondegenerate irreducible subquotient of the induced representation
$\unicode[STIX]{x1D70E}_{0}$
is the unique nondegenerate irreducible subquotient of the induced representation
![]() $\unicode[STIX]{x1D70E}_{1}\times \cdots \times \unicode[STIX]{x1D70E}_{1}$
, where
$\unicode[STIX]{x1D70E}_{1}\times \cdots \times \unicode[STIX]{x1D70E}_{1}$
, where
![]() $\unicode[STIX]{x1D70E}_{1}$
is the supercuspidal mod-
$\unicode[STIX]{x1D70E}_{1}$
is the supercuspidal mod-
![]() $\ell$
representation of
$\ell$
representation of
![]() $\text{GL}_{m\text{sp}\prime /t}(\boldsymbol{d})$
corresponding to
$\text{GL}_{m\text{sp}\prime /t}(\boldsymbol{d})$
corresponding to
![]() $\unicode[STIX]{x1D719}$
. Moreover, if
$\unicode[STIX]{x1D719}$
. Moreover, if
![]() $\unicode[STIX]{x1D705}_{1}$
denotes the maximal
$\unicode[STIX]{x1D705}_{1}$
denotes the maximal
![]() $\unicode[STIX]{x1D6FD}$
-extension of
$\unicode[STIX]{x1D6FD}$
-extension of
![]() $\text{GL}_{m/t}(\text{D})$
such that the representation of
$\text{GL}_{m/t}(\text{D})$
such that the representation of
![]() $\text{J}_{t}\,\cap \,\text{M}_{t}$
on the
$\text{J}_{t}\,\cap \,\text{M}_{t}$
on the
![]() $\text{J}_{t}\,\cap \,\text{U}_{t}$
-invariant subspace of
$\text{J}_{t}\,\cap \,\text{U}_{t}$
-invariant subspace of
![]() $\unicode[STIX]{x1D705}_{t}$
is
$\unicode[STIX]{x1D705}_{t}$
is
![]() $\unicode[STIX]{x1D705}_{1}\otimes \cdots \otimes \unicode[STIX]{x1D705}_{1}$
, then
$\unicode[STIX]{x1D705}_{1}\otimes \cdots \otimes \unicode[STIX]{x1D705}_{1}$
, then
![]() $\unicode[STIX]{x1D705}_{1}\,\otimes \,\unicode[STIX]{x1D70E}_{1}$
is a maximal simple type contained in
$\unicode[STIX]{x1D705}_{1}\,\otimes \,\unicode[STIX]{x1D70E}_{1}$
is a maximal simple type contained in
![]() $\unicode[STIX]{x1D70F}$
. The result follows.◻
$\unicode[STIX]{x1D70F}$
. The result follows.◻
We keep in mind the following straightforward but important fact.
Remark 4.7. Two simple irreducible
![]() $\ell$
-adic representations of
$\ell$
-adic representations of
![]() $\text{G}$
in the same
$\text{G}$
in the same
![]() $\ell$
-block have the same endo-class.
$\ell$
-block have the same endo-class.
The converse does not hold in general, but we have the following result. Given
![]() $\unicode[STIX]{x1D6FC}\in \text{X}$
, write
$\unicode[STIX]{x1D6FC}\in \text{X}$
, write
![]() $[\unicode[STIX]{x1D6FC}]$
for its
$[\unicode[STIX]{x1D6FC}]$
for its
![]() $\unicode[STIX]{x1D6E4}$
-orbit and
$\unicode[STIX]{x1D6E4}$
-orbit and
![]() $\unicode[STIX]{x1D719}$
for its reduction mod
$\unicode[STIX]{x1D719}$
for its reduction mod
![]() $\ell$
. The orbit
$\ell$
. The orbit
![]() $[\unicode[STIX]{x1D719}]$
depends only on
$[\unicode[STIX]{x1D719}]$
depends only on
![]() $[\unicode[STIX]{x1D6FC}]$
and is called the reduction mod
$[\unicode[STIX]{x1D6FC}]$
and is called the reduction mod
![]() $\ell$
of
$\ell$
of
![]() $[\unicode[STIX]{x1D6FC}]$
.
$[\unicode[STIX]{x1D6FC}]$
.
Proposition 4.8. Two simple irreducible
![]() $\ell$
-adic representations of
$\ell$
-adic representations of
![]() $\text{G}$
of endo-class
$\text{G}$
of endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
are in the same
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
are in the same
![]() $\ell$
-block if and only if their parametrizing classes have the same reduction mod
$\ell$
-block if and only if their parametrizing classes have the same reduction mod
![]() $\ell$
.
$\ell$
.
5 Linked complex representations
5.1
We fix a prime number
![]() $\ell$
different from
$\ell$
different from
![]() $p$
and an isomorphism of fields
$p$
and an isomorphism of fields
![]() $\unicode[STIX]{x1D704}_{\ell }:\mathbf{C}\simeq \overline{\mathbf{Q}}_{\ell }$
. If
$\unicode[STIX]{x1D704}_{\ell }:\mathbf{C}\simeq \overline{\mathbf{Q}}_{\ell }$
. If
![]() $\unicode[STIX]{x1D70B}$
is a complex representation of
$\unicode[STIX]{x1D70B}$
is a complex representation of
![]() $\text{G}$
, write
$\text{G}$
, write
![]() $\unicode[STIX]{x1D704}_{\ell }^{\ast }\unicode[STIX]{x1D70B}$
for the
$\unicode[STIX]{x1D704}_{\ell }^{\ast }\unicode[STIX]{x1D70B}$
for the
![]() $\ell$
-adic representation of
$\ell$
-adic representation of
![]() $\text{G}$
obtained by extending scalars from
$\text{G}$
obtained by extending scalars from
![]() $\mathbf{C}$
to
$\mathbf{C}$
to
![]() $\overline{\mathbf{Q}}_{\ell }$
along
$\overline{\mathbf{Q}}_{\ell }$
along
![]() $\unicode[STIX]{x1D704}_{\ell }$
.
$\unicode[STIX]{x1D704}_{\ell }$
.
Definition 5.1. Two irreducible complex representations
![]() $\unicode[STIX]{x1D70B}_{1}$
and
$\unicode[STIX]{x1D70B}_{1}$
and
![]() $\unicode[STIX]{x1D70B}_{2}$
of
$\unicode[STIX]{x1D70B}_{2}$
of
![]() $\text{G}$
are said to be
$\text{G}$
are said to be
![]() $\ell$
-linked if the irreducible
$\ell$
-linked if the irreducible
![]() $\ell$
-adic representations
$\ell$
-adic representations
![]() $\unicode[STIX]{x1D704}_{\ell }^{\ast }\unicode[STIX]{x1D70B}_{1}$
and
$\unicode[STIX]{x1D704}_{\ell }^{\ast }\unicode[STIX]{x1D70B}_{1}$
and
![]() $\unicode[STIX]{x1D704}_{\ell }^{\ast }\unicode[STIX]{x1D70B}_{2}$
are in the same
$\unicode[STIX]{x1D704}_{\ell }^{\ast }\unicode[STIX]{x1D70B}_{2}$
are in the same
![]() $\ell$
-block.
$\ell$
-block.
Lemma 5.2. This definition does not depend on the choice of
![]() $\unicode[STIX]{x1D704}_{\ell }$
.
$\unicode[STIX]{x1D704}_{\ell }$
.
Proof. It is enough to prove that for any field automorphism
![]() $\unicode[STIX]{x1D703}\in \text{Aut}(\overline{\mathbf{Q}}_{\ell })$
, two simple
$\unicode[STIX]{x1D703}\in \text{Aut}(\overline{\mathbf{Q}}_{\ell })$
, two simple
![]() $\ell$
-adic representations
$\ell$
-adic representations
![]() $\widetilde{\unicode[STIX]{x1D70B}}_{1}$
and
$\widetilde{\unicode[STIX]{x1D70B}}_{1}$
and
![]() $\widetilde{\unicode[STIX]{x1D70B}}_{2}$
of
$\widetilde{\unicode[STIX]{x1D70B}}_{2}$
of
![]() $\text{G}$
are in the same
$\text{G}$
are in the same
![]() $\ell$
-block if and only if
$\ell$
-block if and only if
![]() $\widetilde{\unicode[STIX]{x1D70B}}_{1}^{\unicode[STIX]{x1D703}}$
and
$\widetilde{\unicode[STIX]{x1D70B}}_{1}^{\unicode[STIX]{x1D703}}$
and
![]() $\widetilde{\unicode[STIX]{x1D70B}}_{2}^{\unicode[STIX]{x1D703}}$
are in the same
$\widetilde{\unicode[STIX]{x1D70B}}_{2}^{\unicode[STIX]{x1D703}}$
are in the same
![]() $\ell$
-block.
$\ell$
-block.
Given an irreducible
![]() $\ell$
-adic representation
$\ell$
-adic representation
![]() $\widetilde{\unicode[STIX]{x1D70B}}$
, let
$\widetilde{\unicode[STIX]{x1D70B}}$
, let
![]() $(\text{L},\unicode[STIX]{x1D70F})$
be an element of its mod-
$(\text{L},\unicode[STIX]{x1D70F})$
be an element of its mod-
![]() $\ell$
inertial supercuspidal support as in Definition 4.1. Then the mod-
$\ell$
inertial supercuspidal support as in Definition 4.1. Then the mod-
![]() $\ell$
inertial supercuspidal support of the irreducible representation
$\ell$
inertial supercuspidal support of the irreducible representation
![]() $\widetilde{\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D703}}$
is the inertial class of
$\widetilde{\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D703}}$
is the inertial class of
![]() $(\text{L},\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D703}})$
. The result follows.◻
$(\text{L},\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D703}})$
. The result follows.◻
5.2
Recall that we have fixed in § 2 a smooth character
![]() $\unicode[STIX]{x1D713}:\text{F}\rightarrow \mathbf{C}^{\times }$
that is trivial on
$\unicode[STIX]{x1D713}:\text{F}\rightarrow \mathbf{C}^{\times }$
that is trivial on
![]() $\mathfrak{p}$
but not on
$\mathfrak{p}$
but not on
![]() $\mathscr{O}$
. For any simple stratum
$\mathscr{O}$
. For any simple stratum
![]() $[\mathfrak{a},\unicode[STIX]{x1D6FD}]$
, the set of simple complex characters associated with
$[\mathfrak{a},\unicode[STIX]{x1D6FD}]$
, the set of simple complex characters associated with
![]() $[\mathfrak{a},\unicode[STIX]{x1D6FD}]$
will be defined with respect to this choice (see §§ 3.3 and 4.3). We may and will assume that the character
$[\mathfrak{a},\unicode[STIX]{x1D6FD}]$
will be defined with respect to this choice (see §§ 3.3 and 4.3). We may and will assume that the character
![]() $\unicode[STIX]{x1D704}_{\ell }\circ \unicode[STIX]{x1D713}$
is the character
$\unicode[STIX]{x1D704}_{\ell }\circ \unicode[STIX]{x1D713}$
is the character
![]() $\unicode[STIX]{x1D713}_{\ell }$
of § 4.3. This gives us a bijection between endo-classes of complex and
$\unicode[STIX]{x1D713}_{\ell }$
of § 4.3. This gives us a bijection between endo-classes of complex and
![]() $\ell$
-adic simple characters of
$\ell$
-adic simple characters of
![]() $\text{G}$
. Again, we will speak of endo-classes of simple characters, without referring to the coefficient field.
$\text{G}$
. Again, we will speak of endo-classes of simple characters, without referring to the coefficient field.
Let
![]() $\unicode[STIX]{x1D705}$
be a
$\unicode[STIX]{x1D705}$
be a
![]() $\unicode[STIX]{x1D6FD}$
-extension of some maximal complex simple character in
$\unicode[STIX]{x1D6FD}$
-extension of some maximal complex simple character in
![]() $\text{G}$
having endo-class
$\text{G}$
having endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
. Write
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
. Write
![]() $\text{X}$
for the group of complex characters of
$\text{X}$
for the group of complex characters of
![]() $\boldsymbol{k}^{\times }$
.
$\boldsymbol{k}^{\times }$
.
Lemma 5.3. Let
![]() $\unicode[STIX]{x1D70B}$
be a simple irreducible complex representation of
$\unicode[STIX]{x1D70B}$
be a simple irreducible complex representation of
![]() $\text{G}$
with endo-class
$\text{G}$
with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
. Then
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
. Then
Proof. We have
![]() $\unicode[STIX]{x1D6FC}\in \text{X}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D70B})$
if and only if
$\unicode[STIX]{x1D6FC}\in \text{X}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D70B})$
if and only if
![]() $\unicode[STIX]{x1D70B}$
contains the simple type
$\unicode[STIX]{x1D70B}$
contains the simple type
![]() $\boldsymbol{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})=\boldsymbol{\unicode[STIX]{x1D705}}(\unicode[STIX]{x1D6FC})\,\otimes \,\boldsymbol{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D6FC})$
, which occurs if and only if
$\boldsymbol{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})=\boldsymbol{\unicode[STIX]{x1D705}}(\unicode[STIX]{x1D6FC})\,\otimes \,\boldsymbol{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D6FC})$
, which occurs if and only if
![]() $\unicode[STIX]{x1D704}_{\ell }^{\ast }\unicode[STIX]{x1D70B}$
contains the
$\unicode[STIX]{x1D704}_{\ell }^{\ast }\unicode[STIX]{x1D70B}$
contains the
![]() $\ell$
-adic simple type
$\ell$
-adic simple type
![]() $\unicode[STIX]{x1D704}_{\ell }^{\ast }\boldsymbol{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})$
. Thus it suffices to prove that
$\unicode[STIX]{x1D704}_{\ell }^{\ast }\boldsymbol{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})$
. Thus it suffices to prove that
![]() $\unicode[STIX]{x1D704}_{\ell }^{\ast }\boldsymbol{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})$
is equal to
$\unicode[STIX]{x1D704}_{\ell }^{\ast }\boldsymbol{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})$
is equal to
![]() $\widetilde{\boldsymbol{\unicode[STIX]{x1D706}}}_{\ell }(\unicode[STIX]{x1D704}_{\ell }\circ \unicode[STIX]{x1D6FC})$
, where
$\widetilde{\boldsymbol{\unicode[STIX]{x1D706}}}_{\ell }(\unicode[STIX]{x1D704}_{\ell }\circ \unicode[STIX]{x1D6FC})$
, where
![]() $\widetilde{\boldsymbol{\unicode[STIX]{x1D706}}}_{\ell }$
is the map as in § 4.3 defined with respect to the maximal
$\widetilde{\boldsymbol{\unicode[STIX]{x1D706}}}_{\ell }$
is the map as in § 4.3 defined with respect to the maximal
![]() $\unicode[STIX]{x1D6FD}$
-extension
$\unicode[STIX]{x1D6FD}$
-extension
![]() $\unicode[STIX]{x1D704}_{\ell }^{\ast }\unicode[STIX]{x1D705}$
.
$\unicode[STIX]{x1D704}_{\ell }^{\ast }\unicode[STIX]{x1D705}$
.
Firstly, the
![]() $\ell$
-adic
$\ell$
-adic
![]() $\unicode[STIX]{x1D6FD}$
-extension
$\unicode[STIX]{x1D6FD}$
-extension
![]() $\widetilde{\boldsymbol{\unicode[STIX]{x1D705}}}_{\ell }(\unicode[STIX]{x1D704}_{\ell }\circ \unicode[STIX]{x1D6FC})$
associated with
$\widetilde{\boldsymbol{\unicode[STIX]{x1D705}}}_{\ell }(\unicode[STIX]{x1D704}_{\ell }\circ \unicode[STIX]{x1D6FC})$
associated with
![]() $\unicode[STIX]{x1D704}_{\ell }\circ \unicode[STIX]{x1D6FC}$
with respect to
$\unicode[STIX]{x1D704}_{\ell }\circ \unicode[STIX]{x1D6FC}$
with respect to
![]() $\unicode[STIX]{x1D704}_{\ell }^{\ast }\unicode[STIX]{x1D705}$
is equal to
$\unicode[STIX]{x1D704}_{\ell }^{\ast }\unicode[STIX]{x1D705}$
is equal to
![]() $\unicode[STIX]{x1D704}_{\ell }^{\ast }\boldsymbol{\unicode[STIX]{x1D705}}(\unicode[STIX]{x1D6FC})$
. Secondly, the
$\unicode[STIX]{x1D704}_{\ell }^{\ast }\boldsymbol{\unicode[STIX]{x1D705}}(\unicode[STIX]{x1D6FC})$
. Secondly, the
![]() $\ell$
-adic supercuspidal representation
$\ell$
-adic supercuspidal representation
![]() $\widetilde{\boldsymbol{\unicode[STIX]{x1D70E}}}_{\ell }(\unicode[STIX]{x1D704}_{\ell }\circ \unicode[STIX]{x1D6FC})$
associated with
$\widetilde{\boldsymbol{\unicode[STIX]{x1D70E}}}_{\ell }(\unicode[STIX]{x1D704}_{\ell }\circ \unicode[STIX]{x1D6FC})$
associated with
![]() $\unicode[STIX]{x1D704}_{\ell }\circ \unicode[STIX]{x1D6FC}$
(with respect to the choice of an isomorphism (3.3)) is equal to
$\unicode[STIX]{x1D704}_{\ell }\circ \unicode[STIX]{x1D6FC}$
(with respect to the choice of an isomorphism (3.3)) is equal to
![]() $\unicode[STIX]{x1D704}_{\ell }^{\ast }\boldsymbol{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D6FC})$
, since it is characterized by a trace formula (see Remark 3.4). The result follows.◻
$\unicode[STIX]{x1D704}_{\ell }^{\ast }\boldsymbol{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D6FC})$
, since it is characterized by a trace formula (see Remark 3.4). The result follows.◻
Definition 5.4. Let
![]() $\unicode[STIX]{x1D6FC}\in \text{X}$
. The
$\unicode[STIX]{x1D6FC}\in \text{X}$
. The
![]() $\ell$
-regular part of
$\ell$
-regular part of
![]() $\unicode[STIX]{x1D6FC}$
is the unique complex character
$\unicode[STIX]{x1D6FC}$
is the unique complex character
![]() $\unicode[STIX]{x1D6FC}_{\ell }\in \text{X}$
whose order is prime to
$\unicode[STIX]{x1D6FC}_{\ell }\in \text{X}$
whose order is prime to
![]() $\ell$
and such that
$\ell$
and such that
![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}_{\ell }^{-1}$
has order a power of
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}_{\ell }^{-1}$
has order a power of
![]() $\ell$
.
$\ell$
.
Given
![]() $\unicode[STIX]{x1D6FC}\in \text{X}$
, the orbit
$\unicode[STIX]{x1D6FC}\in \text{X}$
, the orbit
![]() $[\unicode[STIX]{x1D6FC}_{\ell }]$
depends only on
$[\unicode[STIX]{x1D6FC}_{\ell }]$
depends only on
![]() $[\unicode[STIX]{x1D6FC}]$
. It is called the
$[\unicode[STIX]{x1D6FC}]$
. It is called the
![]() $\ell$
-regular part of
$\ell$
-regular part of
![]() $[\unicode[STIX]{x1D6FC}]$
, denoted by
$[\unicode[STIX]{x1D6FC}]$
, denoted by
![]() $[\unicode[STIX]{x1D6FC}]_{\ell }$
.
$[\unicode[STIX]{x1D6FC}]_{\ell }$
.
Proposition 5.5. Two simple irreducible complex representations of
![]() $\text{G}$
with endo-class
$\text{G}$
with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
are
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
are
![]() $\ell$
-linked if and only if the
$\ell$
-linked if and only if the
![]() $\ell$
-regular parts of their parametrizing classes are equal.
$\ell$
-regular parts of their parametrizing classes are equal.
Proof. Let
![]() $\unicode[STIX]{x1D70B}_{1}$
and
$\unicode[STIX]{x1D70B}_{1}$
and
![]() $\unicode[STIX]{x1D70B}_{2}$
be simple irreducible complex representations of
$\unicode[STIX]{x1D70B}_{2}$
be simple irreducible complex representations of
![]() $\text{G}$
with endo-class
$\text{G}$
with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
. We fix
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
. We fix
![]() $\unicode[STIX]{x1D6FC}_{i}\in \text{X}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D70B}_{i})$
for each
$\unicode[STIX]{x1D6FC}_{i}\in \text{X}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D70B}_{i})$
for each
![]() $i=1,2$
. By Lemma 5.3 and Proposition 4.8, the representations
$i=1,2$
. By Lemma 5.3 and Proposition 4.8, the representations
![]() $\unicode[STIX]{x1D70B}_{1}$
and
$\unicode[STIX]{x1D70B}_{1}$
and
![]() $\unicode[STIX]{x1D70B}_{2}$
are
$\unicode[STIX]{x1D70B}_{2}$
are
![]() $\ell$
-linked if and only if
$\ell$
-linked if and only if
![]() $[\unicode[STIX]{x1D704}_{\ell }\circ \unicode[STIX]{x1D6FC}_{1}]$
and
$[\unicode[STIX]{x1D704}_{\ell }\circ \unicode[STIX]{x1D6FC}_{1}]$
and
![]() $[\unicode[STIX]{x1D704}_{\ell }\circ \unicode[STIX]{x1D6FC}_{2}]$
have the same reduction mod
$[\unicode[STIX]{x1D704}_{\ell }\circ \unicode[STIX]{x1D6FC}_{2}]$
have the same reduction mod
![]() $\ell$
. But the reduction mod
$\ell$
. But the reduction mod
![]() $\ell$
of
$\ell$
of
![]() $[\unicode[STIX]{x1D704}_{\ell }\circ \unicode[STIX]{x1D6FC}]$
, for a character
$[\unicode[STIX]{x1D704}_{\ell }\circ \unicode[STIX]{x1D6FC}]$
, for a character
![]() $\unicode[STIX]{x1D6FC}\in \text{X}$
, is the same as that of
$\unicode[STIX]{x1D6FC}\in \text{X}$
, is the same as that of
![]() $[\unicode[STIX]{x1D704}_{\ell }\circ \unicode[STIX]{x1D6FC}_{\ell }]$
. It follows that we have
$[\unicode[STIX]{x1D704}_{\ell }\circ \unicode[STIX]{x1D6FC}_{\ell }]$
. It follows that we have
![]() $[\unicode[STIX]{x1D704}_{\ell }\circ (\unicode[STIX]{x1D6FC}_{1})_{\ell }]=[\unicode[STIX]{x1D704}_{\ell }\circ (\unicode[STIX]{x1D6FC}_{2})_{\ell }]$
, so
$[\unicode[STIX]{x1D704}_{\ell }\circ (\unicode[STIX]{x1D6FC}_{1})_{\ell }]=[\unicode[STIX]{x1D704}_{\ell }\circ (\unicode[STIX]{x1D6FC}_{2})_{\ell }]$
, so
![]() $[\unicode[STIX]{x1D6FC}_{1}]_{\ell }=[\unicode[STIX]{x1D6FC}_{2}]_{\ell }$
.◻
$[\unicode[STIX]{x1D6FC}_{1}]_{\ell }=[\unicode[STIX]{x1D6FC}_{2}]_{\ell }$
.◻
5.3
Recall that
![]() $q$
is the cardinality of the residue field of
$q$
is the cardinality of the residue field of
![]() $\text{F}$
. For each prime number
$\text{F}$
. For each prime number
![]() $\ell$
dividing
$\ell$
dividing
we fix an isomorphism of fields
![]() $\unicode[STIX]{x1D704}_{\ell }:\mathbf{C}\simeq \overline{\mathbf{Q}}_{\ell }$
.
$\unicode[STIX]{x1D704}_{\ell }:\mathbf{C}\simeq \overline{\mathbf{Q}}_{\ell }$
.
Definition 5.6. Two irreducible complex representations
![]() $\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}$
and
![]() $\unicode[STIX]{x1D70B}\text{sp}\prime$
of
$\unicode[STIX]{x1D70B}\text{sp}\prime$
of
![]() $\text{G}$
are linked if there are a finite family
$\text{G}$
are linked if there are a finite family
![]() $\ell _{1},\ldots ,\ell _{r}$
of prime numbers dividing (5.1) and a finite family of irreducible complex representations
$\ell _{1},\ldots ,\ell _{r}$
of prime numbers dividing (5.1) and a finite family of irreducible complex representations
![]() $\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{0},\unicode[STIX]{x1D70B}_{1},\ldots ,\unicode[STIX]{x1D70B}_{r}=\unicode[STIX]{x1D70B}\text{sp}\prime$
such that, for all integers
$\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{0},\unicode[STIX]{x1D70B}_{1},\ldots ,\unicode[STIX]{x1D70B}_{r}=\unicode[STIX]{x1D70B}\text{sp}\prime$
such that, for all integers
![]() $i\in \{1,\ldots ,r\}$
, the representations
$i\in \{1,\ldots ,r\}$
, the representations
![]() $\unicode[STIX]{x1D70B}_{i-1}$
and
$\unicode[STIX]{x1D70B}_{i-1}$
and
![]() $\unicode[STIX]{x1D70B}_{i}$
are
$\unicode[STIX]{x1D70B}_{i}$
are
![]() $\ell _{i}$
-linked.
$\ell _{i}$
-linked.
Remark 5.7. By Lemma 5.2, this does not depend on the choice of the isomorphisms
![]() $\unicode[STIX]{x1D704}_{\ell }$
for
$\unicode[STIX]{x1D704}_{\ell }$
for
![]() $\ell$
dividing (5.1).
$\ell$
dividing (5.1).
Two linked simple complex representations of
![]() $\text{G}$
have the same endo-class (see Remark 4.7). The converse is given by the following proposition.
$\text{G}$
have the same endo-class (see Remark 4.7). The converse is given by the following proposition.
Proposition 5.8. Two simple irreducible complex representations are linked if and only if they have the same endo-class.
Proof. Assume that
![]() $\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}$
and
![]() $\unicode[STIX]{x1D70B}\text{sp}\prime$
are simple irreducible complex representations with the same endo-class
$\unicode[STIX]{x1D70B}\text{sp}\prime$
are simple irreducible complex representations with the same endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
. Let
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
. Let
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FC}\text{sp}\prime$
be characters in
$\unicode[STIX]{x1D6FC}\text{sp}\prime$
be characters in
![]() $\text{X}(\unicode[STIX]{x1D70B})$
and
$\text{X}(\unicode[STIX]{x1D70B})$
and
![]() $\text{X}(\unicode[STIX]{x1D70B}\text{sp}\prime )$
, respectively, and write
$\text{X}(\unicode[STIX]{x1D70B}\text{sp}\prime )$
, respectively, and write
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D6FC}\text{sp}\prime \unicode[STIX]{x1D6FC}^{-1}$
. Let
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D6FC}\text{sp}\prime \unicode[STIX]{x1D6FC}^{-1}$
. Let
![]() $\ell _{1},\ldots ,\ell _{r}$
be the prime numbers dividing (5.1). The character
$\ell _{1},\ldots ,\ell _{r}$
be the prime numbers dividing (5.1). The character
![]() $\unicode[STIX]{x1D709}$
decomposes uniquely as
$\unicode[STIX]{x1D709}$
decomposes uniquely as
where the order of
![]() $\unicode[STIX]{x1D709}_{i}$
is a power of
$\unicode[STIX]{x1D709}_{i}$
is a power of
![]() $\ell _{i}$
, for
$\ell _{i}$
, for
![]() $i\in \{1,\ldots ,r\}$
. Write
$i\in \{1,\ldots ,r\}$
. Write
![]() $\unicode[STIX]{x1D6FC}_{0}=\unicode[STIX]{x1D6FC}$
and define inductively
$\unicode[STIX]{x1D6FC}_{0}=\unicode[STIX]{x1D6FC}$
and define inductively
for all
![]() $i\in \{1,\ldots ,r\}$
. Let
$i\in \{1,\ldots ,r\}$
. Let
![]() $\unicode[STIX]{x1D70B}_{i}$
be a simple irreducible complex representation of endo-class
$\unicode[STIX]{x1D70B}_{i}$
be a simple irreducible complex representation of endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
and parametrizing class
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
and parametrizing class
![]() $[\unicode[STIX]{x1D6FC}_{i}]$
. The result follows from Proposition 5.5.◻
$[\unicode[STIX]{x1D6FC}_{i}]$
. The result follows from Proposition 5.5.◻
Remark 5.9. Suppose that
![]() $\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}$
and
![]() $\unicode[STIX]{x1D70B}\text{sp}\prime$
are discrete series representations with the same endo-class. The proof of Proposition 5.8 shows that the simple representations
$\unicode[STIX]{x1D70B}\text{sp}\prime$
are discrete series representations with the same endo-class. The proof of Proposition 5.8 shows that the simple representations
![]() $\unicode[STIX]{x1D70B}_{1},\ldots ,\unicode[STIX]{x1D70B}_{r-1}$
linking
$\unicode[STIX]{x1D70B}_{1},\ldots ,\unicode[STIX]{x1D70B}_{r-1}$
linking
![]() $\unicode[STIX]{x1D70B}$
to
$\unicode[STIX]{x1D70B}$
to
![]() $\unicode[STIX]{x1D70B}\text{sp}\prime$
can be chosen to be discrete series representations as well.
$\unicode[STIX]{x1D70B}\text{sp}\prime$
can be chosen to be discrete series representations as well.
5.4
Let
![]() $\unicode[STIX]{x1D70B}$
be an irreducible complex representation of
$\unicode[STIX]{x1D70B}$
be an irreducible complex representation of
![]() $\text{G}$
. Fix a representative (
$\text{G}$
. Fix a representative (
![]() $\text{M},\unicode[STIX]{x1D70C}$
) in its cuspidal support, with
$\text{M},\unicode[STIX]{x1D70C}$
) in its cuspidal support, with
![]() $\text{M}=\text{GL}_{m_{1}}(\text{D})\times \cdots \times \text{GL}_{m_{r}}(\text{D})$
and
$\text{M}=\text{GL}_{m_{1}}(\text{D})\times \cdots \times \text{GL}_{m_{r}}(\text{D})$
and
![]() $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{1}\otimes \cdots \otimes \unicode[STIX]{x1D70C}_{r}$
, where
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{1}\otimes \cdots \otimes \unicode[STIX]{x1D70C}_{r}$
, where
![]() $\unicode[STIX]{x1D70C}_{i}$
is a cuspidal irreducible representation of
$\unicode[STIX]{x1D70C}_{i}$
is a cuspidal irreducible representation of
![]() $\text{GL}_{m_{i}}(\text{D})$
, for
$\text{GL}_{m_{i}}(\text{D})$
, for
![]() $i\in \{1,\ldots ,r\}$
, and
$i\in \{1,\ldots ,r\}$
, and
![]() $m_{1}+\cdots +m_{r}=m$
. Write
$m_{1}+\cdots +m_{r}=m$
. Write
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}_{i}$
for the endo-class of
$\boldsymbol{\unicode[STIX]{x1D6E9}}_{i}$
for the endo-class of
![]() $\unicode[STIX]{x1D70C}_{i}$
and
$\unicode[STIX]{x1D70C}_{i}$
and
![]() $g_{i}$
for the degree of
$g_{i}$
for the degree of
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}_{i}$
. We define the semi-simple endo-class of
$\boldsymbol{\unicode[STIX]{x1D6E9}}_{i}$
. We define the semi-simple endo-class of
![]() $\unicode[STIX]{x1D70B}$
to be the formal sum
$\unicode[STIX]{x1D70B}$
to be the formal sum
in the free abelian semigroup generated by all
![]() $\text{F}$
-endo-classes. It depends only on the inertial class of the cuspidal support of
$\text{F}$
-endo-classes. It depends only on the inertial class of the cuspidal support of
![]() $\unicode[STIX]{x1D70B}$
.
$\unicode[STIX]{x1D70B}$
.
Note that if
![]() $\unicode[STIX]{x1D70B}$
is a simple irreducible representation with endo-class
$\unicode[STIX]{x1D70B}$
is a simple irreducible representation with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
, then its semi-simple endo-class is
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
, then its semi-simple endo-class is
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}(\unicode[STIX]{x1D70B})=(n/g)\cdot \boldsymbol{\unicode[STIX]{x1D6E9}}$
where
$\boldsymbol{\unicode[STIX]{x1D6E9}}(\unicode[STIX]{x1D70B})=(n/g)\cdot \boldsymbol{\unicode[STIX]{x1D6E9}}$
where
![]() $g$
is the degree of
$g$
is the degree of
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
.
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
.
The following theorem, which is our first main result, generalizes Proposition 5.8.
Theorem 5.10. Two irreducible complex representations are linked if and only if they have the same semi-simple endo-class.
Proof. Any two linked irreducible complex representations automatically have the same semi-simple endo-class. We therefore start with two irreducible complex representations
![]() $\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}$
and
![]() $\unicode[STIX]{x1D70B}\text{sp}\prime$
with the same semi-simple endo-class. By [Reference Mínguez and SécherreMS14b, Théorème 4.16], the representation
$\unicode[STIX]{x1D70B}\text{sp}\prime$
with the same semi-simple endo-class. By [Reference Mínguez and SécherreMS14b, Théorème 4.16], the representation
![]() $\unicode[STIX]{x1D70B}$
can be written as
$\unicode[STIX]{x1D70B}$
can be written as
where
![]() $\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2},\ldots ,\unicode[STIX]{x1D70B}_{k}$
are simple irreducible representations whose inertial cuspidal supports are pairwise distinct, and this decomposition is unique up to renumbering. We have the following straightforward lemma.
$\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2},\ldots ,\unicode[STIX]{x1D70B}_{k}$
are simple irreducible representations whose inertial cuspidal supports are pairwise distinct, and this decomposition is unique up to renumbering. We have the following straightforward lemma.
Lemma 5.11. Let
![]() $\unicode[STIX]{x1D6FF}$
be an irreducible complex representation of
$\unicode[STIX]{x1D6FF}$
be an irreducible complex representation of
![]() $\text{GL}_{m-k}(\text{D})$
for some integer
$\text{GL}_{m-k}(\text{D})$
for some integer
![]() $k\in \{1,\ldots ,m-1\}$
. Let
$k\in \{1,\ldots ,m-1\}$
. Let
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D70E}\text{sp}\prime$
be two irreducible complex representations of
$\unicode[STIX]{x1D70E}\text{sp}\prime$
be two irreducible complex representations of
![]() $\text{GL}_{k}(\text{D})$
, and let
$\text{GL}_{k}(\text{D})$
, and let
![]() $\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}$
and
![]() $\unicode[STIX]{x1D70B}\text{sp}\prime$
be irreducible subquotients of
$\unicode[STIX]{x1D70B}\text{sp}\prime$
be irreducible subquotients of
![]() $\unicode[STIX]{x1D70E}\times \unicode[STIX]{x1D6FF}$
and
$\unicode[STIX]{x1D70E}\times \unicode[STIX]{x1D6FF}$
and
![]() $\unicode[STIX]{x1D70E}\text{sp}\prime \times \unicode[STIX]{x1D6FF}$
, respectively. If
$\unicode[STIX]{x1D70E}\text{sp}\prime \times \unicode[STIX]{x1D6FF}$
, respectively. If
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D70E}\text{sp}\prime$
are linked, then
$\unicode[STIX]{x1D70E}\text{sp}\prime$
are linked, then
![]() $\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}$
and
![]() $\unicode[STIX]{x1D70B}\text{sp}\prime$
are linked.
$\unicode[STIX]{x1D70B}\text{sp}\prime$
are linked.
For each
![]() $i\in \{1,\ldots ,k\}$
, thanks to Lemma 5.11 and Proposition 5.8 we may and will assume that
$i\in \{1,\ldots ,k\}$
, thanks to Lemma 5.11 and Proposition 5.8 we may and will assume that
![]() $\unicode[STIX]{x1D70B}_{i}$
is a discrete series representation of the form
$\unicode[STIX]{x1D70B}_{i}$
is a discrete series representation of the form
![]() $\text{L}(\unicode[STIX]{x1D70C}_{i},r_{i})$
for some cuspidal representation
$\text{L}(\unicode[STIX]{x1D70C}_{i},r_{i})$
for some cuspidal representation
![]() $\unicode[STIX]{x1D70C}_{i}$
of
$\unicode[STIX]{x1D70C}_{i}$
of
![]() $\text{GL}_{m_{i}}(\text{D})$
with the same endo-class as
$\text{GL}_{m_{i}}(\text{D})$
with the same endo-class as
![]() $\unicode[STIX]{x1D70B}_{i}$
and for some integer
$\unicode[STIX]{x1D70B}_{i}$
and for some integer
![]() $r_{i}$
, such that
$r_{i}$
, such that
![]() $m_{1}r_{1}+\cdots +m_{k}r_{k}=m$
. We may even assume that
$m_{1}r_{1}+\cdots +m_{k}r_{k}=m$
. We may even assume that
![]() $\unicode[STIX]{x1D70C}_{i}$
has minimal degree among all cuspidal irreducible representations of
$\unicode[STIX]{x1D70C}_{i}$
has minimal degree among all cuspidal irreducible representations of
![]() $\text{GL}_{a}(\text{D})$
,
$\text{GL}_{a}(\text{D})$
,
![]() $a\geqslant 1$
, with the same endo-class as
$a\geqslant 1$
, with the same endo-class as
![]() $\unicode[STIX]{x1D70B}_{i}$
. This amounts to saying that
$\unicode[STIX]{x1D70B}_{i}$
. This amounts to saying that
![]() $m_{i}$
is equal to
$m_{i}$
is equal to
![]() $g_{i}/(g_{i},d)$
, where
$g_{i}/(g_{i},d)$
, where
![]() $g_{i}$
is the degree of the endo-class of
$g_{i}$
is the degree of the endo-class of
![]() $\unicode[STIX]{x1D70B}_{i}$
.
$\unicode[STIX]{x1D70B}_{i}$
.
Moreover, if
![]() $\unicode[STIX]{x1D70C}_{i}$
and
$\unicode[STIX]{x1D70C}_{i}$
and
![]() $\unicode[STIX]{x1D70C}_{j}$
have the same endo-class for some
$\unicode[STIX]{x1D70C}_{j}$
have the same endo-class for some
![]() $i,j\in \{1,\ldots ,k\}$
, then they have the same degree, and so they are linked. We may thus assume that
$i,j\in \{1,\ldots ,k\}$
, then they have the same degree, and so they are linked. We may thus assume that
![]() $\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{k}$
have distinct endo-classes, denoted by
$\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{k}$
have distinct endo-classes, denoted by
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}_{1},\ldots ,\boldsymbol{\unicode[STIX]{x1D6E9}}_{k}$
, respectively.
$\boldsymbol{\unicode[STIX]{x1D6E9}}_{1},\ldots ,\boldsymbol{\unicode[STIX]{x1D6E9}}_{k}$
, respectively.
Similarly, we may assume that the representation
![]() $\unicode[STIX]{x1D70B}\text{sp}\prime$
decomposes as a product
$\unicode[STIX]{x1D70B}\text{sp}\prime$
decomposes as a product
![]() $\unicode[STIX]{x1D70B}\text{sp}\prime _{1}\times \unicode[STIX]{x1D70B}\text{sp}\prime _{2}\times \cdots \times \unicode[STIX]{x1D70B}\text{sp}\prime _{t}$
, where
$\unicode[STIX]{x1D70B}\text{sp}\prime _{1}\times \unicode[STIX]{x1D70B}\text{sp}\prime _{2}\times \cdots \times \unicode[STIX]{x1D70B}\text{sp}\prime _{t}$
, where
![]() $\unicode[STIX]{x1D70B}\text{sp}\prime _{j}$
is a discrete series representation of the form
$\unicode[STIX]{x1D70B}\text{sp}\prime _{j}$
is a discrete series representation of the form
![]() $\text{L}(\unicode[STIX]{x1D70C}_{j}^{\prime },s_{j}^{})$
for some cuspidal representation
$\text{L}(\unicode[STIX]{x1D70C}_{j}^{\prime },s_{j}^{})$
for some cuspidal representation
![]() $\unicode[STIX]{x1D70C}\text{sp}\prime _{j}$
of
$\unicode[STIX]{x1D70C}\text{sp}\prime _{j}$
of
![]() $\text{GL}_{m_{j}^{\prime }}(\text{D})$
and some integer
$\text{GL}_{m_{j}^{\prime }}(\text{D})$
and some integer
![]() $s_{j}^{}\geqslant 1$
, and we may assume that the endo-classes
$s_{j}^{}\geqslant 1$
, and we may assume that the endo-classes
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}\text{sp}\prime _{1},\ldots ,\boldsymbol{\unicode[STIX]{x1D6E9}}\text{sp}\prime _{t}$
of
$\boldsymbol{\unicode[STIX]{x1D6E9}}\text{sp}\prime _{1},\ldots ,\boldsymbol{\unicode[STIX]{x1D6E9}}\text{sp}\prime _{t}$
of
![]() $\unicode[STIX]{x1D70C}_{1}^{\prime },\ldots ,\unicode[STIX]{x1D70C}_{t}^{\prime }$
are distinct. It follows that
$\unicode[STIX]{x1D70C}_{1}^{\prime },\ldots ,\unicode[STIX]{x1D70C}_{t}^{\prime }$
are distinct. It follows that
![]() $k=t$
and, up to renumbering, we may assume that we have
$k=t$
and, up to renumbering, we may assume that we have
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}_{i}^{\prime }=\boldsymbol{\unicode[STIX]{x1D6E9}}_{i}^{}$
for each
$\boldsymbol{\unicode[STIX]{x1D6E9}}_{i}^{\prime }=\boldsymbol{\unicode[STIX]{x1D6E9}}_{i}^{}$
for each
![]() $i\in \{1,\ldots ,k\}$
. It then follows that
$i\in \{1,\ldots ,k\}$
. It then follows that
![]() $\unicode[STIX]{x1D70C}\text{sp}\prime _{i}$
and
$\unicode[STIX]{x1D70C}\text{sp}\prime _{i}$
and
![]() $\unicode[STIX]{x1D70C}_{i}^{}$
have the same degree by minimality of
$\unicode[STIX]{x1D70C}_{i}^{}$
have the same degree by minimality of
![]() $m_{i}$
.
$m_{i}$
.
Since
![]() $\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}$
and
![]() $\unicode[STIX]{x1D70B}\text{sp}\prime$
have the same semi-simple endo-class, we have
$\unicode[STIX]{x1D70B}\text{sp}\prime$
have the same semi-simple endo-class, we have
![]() $s_{i}=r_{i}$
for all
$s_{i}=r_{i}$
for all
![]() $i$
, so
$i$
, so
![]() $\unicode[STIX]{x1D70B}_{i}^{}$
and
$\unicode[STIX]{x1D70B}_{i}^{}$
and
![]() $\unicode[STIX]{x1D70B}\text{sp}\prime _{i}$
have the same degree. Proposition 5.8 then implies that
$\unicode[STIX]{x1D70B}\text{sp}\prime _{i}$
have the same degree. Proposition 5.8 then implies that
![]() $\unicode[STIX]{x1D70B}_{i}^{}$
and
$\unicode[STIX]{x1D70B}_{i}^{}$
and
![]() $\unicode[STIX]{x1D70B}\text{sp}\prime _{i}$
are linked. Theorem 5.10 now follows from Lemma 5.11 again.◻
$\unicode[STIX]{x1D70B}\text{sp}\prime _{i}$
are linked. Theorem 5.10 now follows from Lemma 5.11 again.◻
6 Application to the local Jacquet–Langlands correspondence
We fix
![]() $n=md$
and write
$n=md$
and write
![]() $\text{G}=\text{GL}_{m}(\text{D})$
and
$\text{G}=\text{GL}_{m}(\text{D})$
and
![]() $\text{H}=\text{GL}_{n}(\text{F})$
. As in the introduction, we write
$\text{H}=\text{GL}_{n}(\text{F})$
. As in the introduction, we write
![]() $\mathscr{D}(\text{G},\mathbf{C})$
for the set of all isomorphism classes of complex discrete series representations of
$\mathscr{D}(\text{G},\mathbf{C})$
for the set of all isomorphism classes of complex discrete series representations of
![]() $\text{G}$
, and similarly for
$\text{G}$
, and similarly for
![]() $\text{H}$
. We write
$\text{H}$
. We write
for the local Jacquet–Langlands correspondence.
6.1
We fix an isomorphism of fields
![]() $\unicode[STIX]{x1D704}_{\ell }:\mathbf{C}\simeq \overline{\mathbf{Q}}_{\ell }$
and write (as in [Reference Mínguez and SécherreMS17])
$\unicode[STIX]{x1D704}_{\ell }:\mathbf{C}\simeq \overline{\mathbf{Q}}_{\ell }$
and write (as in [Reference Mínguez and SécherreMS17])
for the
![]() $\ell$
-adic local Jacquet–Langlands correspondence between
$\ell$
-adic local Jacquet–Langlands correspondence between
![]() $\ell$
-adic discrete series representations of
$\ell$
-adic discrete series representations of
![]() $\text{G}$
and
$\text{G}$
and
![]() $\text{H}$
. The correspondence (6.2) does not depend on the choice of
$\text{H}$
. The correspondence (6.2) does not depend on the choice of
![]() $\unicode[STIX]{x1D704}_{\ell }$
(see [Reference Mínguez and SécherreMS17, Remarque 10.1]). According to [Reference BadulescuBad07, § 3.1], there is a unique surjective group homomorphism
$\unicode[STIX]{x1D704}_{\ell }$
(see [Reference Mínguez and SécherreMS17, Remarque 10.1]). According to [Reference BadulescuBad07, § 3.1], there is a unique surjective group homomorphism
where
![]() $\mathscr{R}(\text{G},\overline{\mathbf{Q}}_{\ell })$
is the Grothendieck group of finite-length
$\mathscr{R}(\text{G},\overline{\mathbf{Q}}_{\ell })$
is the Grothendieck group of finite-length
![]() $\ell$
-adic representations of
$\ell$
-adic representations of
![]() $\text{G}$
, with the following property: given positive integers
$\text{G}$
, with the following property: given positive integers
![]() $n_{1},\ldots ,n_{r}$
such that
$n_{1},\ldots ,n_{r}$
such that
![]() $n_{1}+\cdots +n_{r}=n$
and an
$n_{1}+\cdots +n_{r}=n$
and an
![]() $\ell$
-adic discrete series representation
$\ell$
-adic discrete series representation
![]() $\widetilde{\unicode[STIX]{x1D70E}}_{i}$
of
$\widetilde{\unicode[STIX]{x1D70E}}_{i}$
of
![]() $\text{GL}_{n_{i}}(\text{F})$
for each
$\text{GL}_{n_{i}}(\text{F})$
for each
![]() $i$
, the image of the product
$i$
, the image of the product
![]() $\widetilde{\unicode[STIX]{x1D70E}}_{1}\times \cdots \times \widetilde{\unicode[STIX]{x1D70E}}_{r}$
by
$\widetilde{\unicode[STIX]{x1D70E}}_{1}\times \cdots \times \widetilde{\unicode[STIX]{x1D70E}}_{r}$
by
![]() $\widetilde{\text{}\text{J}}_{\ell }$
is
$\widetilde{\text{}\text{J}}_{\ell }$
is
![]() $0$
if
$0$
if
![]() $n_{i}$
is not divisible by
$n_{i}$
is not divisible by
![]() $d$
for at least one
$d$
for at least one
![]() $i$
, and is
$i$
, and is
![]() $\widetilde{\unicode[STIX]{x1D70B}}_{1}\times \cdots \times \widetilde{\unicode[STIX]{x1D70B}}_{r}$
otherwise, where
$\widetilde{\unicode[STIX]{x1D70B}}_{1}\times \cdots \times \widetilde{\unicode[STIX]{x1D70B}}_{r}$
otherwise, where
![]() $n_{i}=m_{i}d$
and
$n_{i}=m_{i}d$
and
![]() $\widetilde{\unicode[STIX]{x1D70B}}_{i}$
is the
$\widetilde{\unicode[STIX]{x1D70B}}_{i}$
is the
![]() $\ell$
-adic discrete series representation of
$\ell$
-adic discrete series representation of
![]() $\text{GL}_{m_{i}}(\text{D})$
whose Jacquet–Langlands transfer is
$\text{GL}_{m_{i}}(\text{D})$
whose Jacquet–Langlands transfer is
![]() $\widetilde{\unicode[STIX]{x1D70E}}_{i}$
for each
$\widetilde{\unicode[STIX]{x1D70E}}_{i}$
for each
![]() $i$
.
$i$
.
By [Reference Mínguez and SécherreMS17, Théorème 12.4], there exists a unique surjective group homomorphism of Grothendieck groups
![]() $\text{}\text{J}_{\ell }:\mathscr{R}(\text{H},\overline{\mathbf{F}}_{\ell })\rightarrow \mathscr{R}(\text{G},\overline{\mathbf{F}}_{\ell })$
such that the diagram
$\text{}\text{J}_{\ell }:\mathscr{R}(\text{H},\overline{\mathbf{F}}_{\ell })\rightarrow \mathscr{R}(\text{G},\overline{\mathbf{F}}_{\ell })$
such that the diagram

is commutative, where
![]() $\mathscr{R}(\text{G},\overline{\mathbf{Q}}_{\ell })^{\text{e}}$
is the subgroup of
$\mathscr{R}(\text{G},\overline{\mathbf{Q}}_{\ell })^{\text{e}}$
is the subgroup of
![]() $\mathscr{R}(\text{G},\overline{\mathbf{Q}}_{\ell })$
generated by integral irreducible representations and
$\mathscr{R}(\text{G},\overline{\mathbf{Q}}_{\ell })$
generated by integral irreducible representations and
![]() $\mathscr{R}(\text{G},\overline{\mathbf{F}}_{\ell })$
is the Grothendieck group of
$\mathscr{R}(\text{G},\overline{\mathbf{F}}_{\ell })$
is the Grothendieck group of
![]() $\ell$
-modular representations of
$\ell$
-modular representations of
![]() $\text{G}$
.
$\text{G}$
.
Proposition 6.1. Let
![]() $\widetilde{\unicode[STIX]{x1D70B}}_{1}$
and
$\widetilde{\unicode[STIX]{x1D70B}}_{1}$
and
![]() $\widetilde{\unicode[STIX]{x1D70B}}_{2}$
be
$\widetilde{\unicode[STIX]{x1D70B}}_{2}$
be
![]() $\ell$
-adic discrete series representations of
$\ell$
-adic discrete series representations of
![]() $\text{G}$
, and write
$\text{G}$
, and write
![]() $\widetilde{\unicode[STIX]{x1D70E}}_{1}$
and
$\widetilde{\unicode[STIX]{x1D70E}}_{1}$
and
![]() $\widetilde{\unicode[STIX]{x1D70E}}_{2}$
for their Jacquet–Langlands transfers to
$\widetilde{\unicode[STIX]{x1D70E}}_{2}$
for their Jacquet–Langlands transfers to
![]() $\text{H}$
, respectively. If
$\text{H}$
, respectively. If
![]() $\widetilde{\unicode[STIX]{x1D70E}}_{1}$
and
$\widetilde{\unicode[STIX]{x1D70E}}_{1}$
and
![]() $\widetilde{\unicode[STIX]{x1D70E}}_{2}$
are in the same
$\widetilde{\unicode[STIX]{x1D70E}}_{2}$
are in the same
![]() $\ell$
-block of
$\ell$
-block of
![]() $\text{H}$
, then
$\text{H}$
, then
![]() $\widetilde{\unicode[STIX]{x1D70B}}_{1}$
and
$\widetilde{\unicode[STIX]{x1D70B}}_{1}$
and
![]() $\widetilde{\unicode[STIX]{x1D70B}}_{2}$
are in the same
$\widetilde{\unicode[STIX]{x1D70B}}_{2}$
are in the same
![]() $\ell$
-block of
$\ell$
-block of
![]() $\text{G}$
.
$\text{G}$
.
Proof. Let us write
![]() $\widetilde{\unicode[STIX]{x1D70E}}_{i}=\text{L}(\widetilde{\unicode[STIX]{x1D70C}}_{i},r_{i})$
and
$\widetilde{\unicode[STIX]{x1D70E}}_{i}=\text{L}(\widetilde{\unicode[STIX]{x1D70C}}_{i},r_{i})$
and
![]() $k_{i}=k(\widetilde{\unicode[STIX]{x1D70C}}_{i})$
for
$k_{i}=k(\widetilde{\unicode[STIX]{x1D70C}}_{i})$
for
![]() $i=1,2$
. Then
$i=1,2$
. Then
![]() $k_{1}r_{1}=k_{2}r_{2}$
, which we denote by
$k_{1}r_{1}=k_{2}r_{2}$
, which we denote by
![]() $v$
, and the mod-
$v$
, and the mod-
![]() $\ell$
inertial supercuspidal support of
$\ell$
inertial supercuspidal support of
![]() $\widetilde{\unicode[STIX]{x1D70E}}_{1}$
and
$\widetilde{\unicode[STIX]{x1D70E}}_{1}$
and
![]() $\widetilde{\unicode[STIX]{x1D70E}}_{2}$
contains the supercuspidal pair
$\widetilde{\unicode[STIX]{x1D70E}}_{2}$
contains the supercuspidal pair
with
![]() $uv=m$
and for some mod-
$uv=m$
and for some mod-
![]() $\ell$
supercuspidal representation
$\ell$
supercuspidal representation
![]() $\unicode[STIX]{x1D70F}$
of
$\unicode[STIX]{x1D70F}$
of
![]() $\text{GL}_{u}(\text{D})$
. Fix an
$\text{GL}_{u}(\text{D})$
. Fix an
![]() $\ell$
-adic lift
$\ell$
-adic lift
![]() $\widetilde{\unicode[STIX]{x1D70F}}$
of
$\widetilde{\unicode[STIX]{x1D70F}}$
of
![]() $\unicode[STIX]{x1D70F}$
and write
$\unicode[STIX]{x1D70F}$
and write
![]() $\widetilde{\unicode[STIX]{x1D70E}}=\text{L}(\widetilde{\unicode[STIX]{x1D70F}},v)$
. The representation
$\widetilde{\unicode[STIX]{x1D70E}}=\text{L}(\widetilde{\unicode[STIX]{x1D70F}},v)$
. The representation
![]() $\widetilde{\unicode[STIX]{x1D70E}}$
is in the same
$\widetilde{\unicode[STIX]{x1D70E}}$
is in the same
![]() $\ell$
-block as
$\ell$
-block as
![]() $\widetilde{\unicode[STIX]{x1D70E}}_{1}$
and
$\widetilde{\unicode[STIX]{x1D70E}}_{1}$
and
![]() $\widetilde{\unicode[STIX]{x1D70E}}_{2}$
, by Lemma 4.5. If we write
$\widetilde{\unicode[STIX]{x1D70E}}_{2}$
, by Lemma 4.5. If we write
![]() $\widetilde{\unicode[STIX]{x1D70B}}$
for the
$\widetilde{\unicode[STIX]{x1D70B}}$
for the
![]() $\ell$
-adic discrete series representation of
$\ell$
-adic discrete series representation of
![]() $\text{G}$
whose transfer to
$\text{G}$
whose transfer to
![]() $\text{H}$
is
$\text{H}$
is
![]() $\widetilde{\unicode[STIX]{x1D70E}}$
, then it is enough to prove that
$\widetilde{\unicode[STIX]{x1D70E}}$
, then it is enough to prove that
![]() $\widetilde{\unicode[STIX]{x1D70B}}$
is in the same
$\widetilde{\unicode[STIX]{x1D70B}}$
is in the same
![]() $\ell$
-block as
$\ell$
-block as
![]() $\widetilde{\unicode[STIX]{x1D70B}}_{1}$
.
$\widetilde{\unicode[STIX]{x1D70B}}_{1}$
.
In the remainder of the proof, it will be more convenient to deal with Speh representations than with discrete series representations, as in [Reference Mínguez and SécherreMS17]. We therefore apply the Zelevinski involution to
![]() $\widetilde{\unicode[STIX]{x1D70B}},\widetilde{\unicode[STIX]{x1D70B}}_{1}$
and
$\widetilde{\unicode[STIX]{x1D70B}},\widetilde{\unicode[STIX]{x1D70B}}_{1}$
and
![]() $\widetilde{\unicode[STIX]{x1D70E}},\widetilde{\unicode[STIX]{x1D70E}}_{1}$
and thus get
$\widetilde{\unicode[STIX]{x1D70E}},\widetilde{\unicode[STIX]{x1D70E}}_{1}$
and thus get
![]() $\ell$
-adic Speh representations.
$\ell$
-adic Speh representations.
Let us write
![]() $\widetilde{\unicode[STIX]{x1D70E}}^{\ast }$
for the Zelevinski dual of
$\widetilde{\unicode[STIX]{x1D70E}}^{\ast }$
for the Zelevinski dual of
![]() $\widetilde{\unicode[STIX]{x1D70E}}$
. Its reduction mod
$\widetilde{\unicode[STIX]{x1D70E}}$
. Its reduction mod
![]() $\ell$
is the
$\ell$
is the
![]() $\ell$
-modular super-Speh representation
$\ell$
-modular super-Speh representation
![]() $\text{Z}(\unicode[STIX]{x1D70F},v)$
, by [Reference Mínguez and SécherreMS14a, Théorème 9.39]. If we write
$\text{Z}(\unicode[STIX]{x1D70F},v)$
, by [Reference Mínguez and SécherreMS14a, Théorème 9.39]. If we write
![]() $\widetilde{\unicode[STIX]{x1D70B}}^{\ast }=\text{Z}(\widetilde{\unicode[STIX]{x1D6FC}},t)$
for the Zelevinski dual of
$\widetilde{\unicode[STIX]{x1D70B}}^{\ast }=\text{Z}(\widetilde{\unicode[STIX]{x1D6FC}},t)$
for the Zelevinski dual of
![]() $\widetilde{\unicode[STIX]{x1D70B}}$
, for some
$\widetilde{\unicode[STIX]{x1D70B}}$
, for some
![]() $t$
dividing
$t$
dividing
![]() $m$
and some cuspidal irreducible representation
$m$
and some cuspidal irreducible representation
![]() $\widetilde{\unicode[STIX]{x1D6FC}}$
of
$\widetilde{\unicode[STIX]{x1D6FC}}$
of
![]() $\text{GL}_{m/t}(\text{D})$
, then its reduction mod
$\text{GL}_{m/t}(\text{D})$
, then its reduction mod
![]() $\ell$
contains the Speh representation
$\ell$
contains the Speh representation
![]() $\text{Z}(\unicode[STIX]{x1D6FC},t)$
where
$\text{Z}(\unicode[STIX]{x1D6FC},t)$
where
![]() $\unicode[STIX]{x1D6FC}$
is an irreducible component of the reduction mod
$\unicode[STIX]{x1D6FC}$
is an irreducible component of the reduction mod
![]() $\ell$
of
$\ell$
of
![]() $\widetilde{\unicode[STIX]{x1D6FC}}$
(see for instance [Reference Mínguez and SécherreMS17, Proposition 1.10]). The cuspidal representation
$\widetilde{\unicode[STIX]{x1D6FC}}$
(see for instance [Reference Mínguez and SécherreMS17, Proposition 1.10]). The cuspidal representation
![]() $\unicode[STIX]{x1D6FC}$
need not be supercuspidal but, according to Proposition 3.1, it can be written as
$\unicode[STIX]{x1D6FC}$
need not be supercuspidal but, according to Proposition 3.1, it can be written as
![]() $\text{Sp}(\unicode[STIX]{x1D6FD},k)$
for
$\text{Sp}(\unicode[STIX]{x1D6FD},k)$
for
![]() $k=k(\unicode[STIX]{x1D6FC})$
and some supercuspidal irreducible representation
$k=k(\unicode[STIX]{x1D6FC})$
and some supercuspidal irreducible representation
![]() $\unicode[STIX]{x1D6FD}$
.
$\unicode[STIX]{x1D6FD}$
.
We now look at the reduction mod
![]() $\ell$
of the Zelevinski dual of
$\ell$
of the Zelevinski dual of
![]() $\widetilde{\unicode[STIX]{x1D70E}}_{1}$
. It is
$\widetilde{\unicode[STIX]{x1D70E}}_{1}$
. It is
![]() $\text{Z}(\unicode[STIX]{x1D70C}_{1},r_{1})$
where
$\text{Z}(\unicode[STIX]{x1D70C}_{1},r_{1})$
where
![]() $\unicode[STIX]{x1D70C}_{1}$
, the reduction mod
$\unicode[STIX]{x1D70C}_{1}$
, the reduction mod
![]() $\ell$
of
$\ell$
of
![]() $\widetilde{\unicode[STIX]{x1D70C}}_{1}$
, can be written as
$\widetilde{\unicode[STIX]{x1D70C}}_{1}$
, can be written as
![]() $\text{Sp}(\unicode[STIX]{x1D70F}\unicode[STIX]{x1D712},k_{1})$
for some unramified character
$\text{Sp}(\unicode[STIX]{x1D70F}\unicode[STIX]{x1D712},k_{1})$
for some unramified character
![]() $\unicode[STIX]{x1D712}$
. By twisting
$\unicode[STIX]{x1D712}$
. By twisting
![]() $\widetilde{\unicode[STIX]{x1D70B}}_{1}$
by an unramified character of
$\widetilde{\unicode[STIX]{x1D70B}}_{1}$
by an unramified character of
![]() $\text{G}$
, we may assume that
$\text{G}$
, we may assume that
![]() $\unicode[STIX]{x1D712}$
is trivial. According to [Reference Mínguez and SécherreMS14a, Lemme 9.41], the representation
$\unicode[STIX]{x1D712}$
is trivial. According to [Reference Mínguez and SécherreMS14a, Lemme 9.41], the representation
![]() $\text{Z}(\unicode[STIX]{x1D70C}_{1},k_{1})$
decomposes as a
$\text{Z}(\unicode[STIX]{x1D70C}_{1},k_{1})$
decomposes as a
![]() $\mathbf{Z}$
-linear combination of products of the form
$\mathbf{Z}$
-linear combination of products of the form
with
![]() $v_{1}+\cdots +v_{r}=v$
and
$v_{1}+\cdots +v_{r}=v$
and
![]() $i_{1},\ldots ,i_{r}\in \mathbf{Z}$
, where
$i_{1},\ldots ,i_{r}\in \mathbf{Z}$
, where
![]() $\unicode[STIX]{x1D708}$
stands for the absolute value of the reduced norm, as usual. (For an explicit formula for this decomposition, see [Reference Mínguez and SécherreMS17, §§ 11 and 12].) Thanks to the commutative diagram above, the reduction modulo
$\unicode[STIX]{x1D708}$
stands for the absolute value of the reduced norm, as usual. (For an explicit formula for this decomposition, see [Reference Mínguez and SécherreMS17, §§ 11 and 12].) Thanks to the commutative diagram above, the reduction modulo
![]() $\ell$
of the Zelevinski dual of
$\ell$
of the Zelevinski dual of
![]() $\widetilde{\unicode[STIX]{x1D70B}}_{1}$
will be made of products of the form
$\widetilde{\unicode[STIX]{x1D70B}}_{1}$
will be made of products of the form
with
![]() $t_{1}+\cdots +t_{r}=t$
and
$t_{1}+\cdots +t_{r}=t$
and
![]() $i_{1},\ldots ,i_{r}\in \mathbf{Z}$
, all of whose irreducible subquotients have supercuspidal support inertially equivalent to
$i_{1},\ldots ,i_{r}\in \mathbf{Z}$
, all of whose irreducible subquotients have supercuspidal support inertially equivalent to
![]() $(\text{GL}_{w}(\text{D})\times \cdots \times \text{GL}_{w}(\text{D}),\unicode[STIX]{x1D6FD}\otimes \cdots \otimes \unicode[STIX]{x1D6FD})$
with
$(\text{GL}_{w}(\text{D})\times \cdots \times \text{GL}_{w}(\text{D}),\unicode[STIX]{x1D6FD}\otimes \cdots \otimes \unicode[STIX]{x1D6FD})$
with
![]() $wkt=m$
. The result follows from Corollary 4.4.◻
$wkt=m$
. The result follows from Corollary 4.4.◻
6.2
Proposition 6.1 implies that two complex discrete series representations
![]() $\unicode[STIX]{x1D70B}_{1}$
and
$\unicode[STIX]{x1D70B}_{1}$
and
![]() $\unicode[STIX]{x1D70B}_{2}$
of
$\unicode[STIX]{x1D70B}_{2}$
of
![]() $\text{G}$
are linked if their Jacquet–Langlands transfers are linked. We have the following refinement.
$\text{G}$
are linked if their Jacquet–Langlands transfers are linked. We have the following refinement.
Proposition 6.2. Let
![]() $\widetilde{\unicode[STIX]{x1D70B}}_{1}$
and
$\widetilde{\unicode[STIX]{x1D70B}}_{1}$
and
![]() $\widetilde{\unicode[STIX]{x1D70B}}_{2}$
be
$\widetilde{\unicode[STIX]{x1D70B}}_{2}$
be
![]() $\ell$
-adic discrete series representations of
$\ell$
-adic discrete series representations of
![]() $\text{G}$
, and write
$\text{G}$
, and write
![]() $\widetilde{\unicode[STIX]{x1D70E}}_{1}$
and
$\widetilde{\unicode[STIX]{x1D70E}}_{1}$
and
![]() $\widetilde{\unicode[STIX]{x1D70E}}_{2}$
for their Jacquet–Langlands transfers to
$\widetilde{\unicode[STIX]{x1D70E}}_{2}$
for their Jacquet–Langlands transfers to
![]() $\text{H}$
, respectively. Then
$\text{H}$
, respectively. Then
![]() $\widetilde{\unicode[STIX]{x1D70E}}_{1}$
and
$\widetilde{\unicode[STIX]{x1D70E}}_{1}$
and
![]() $\widetilde{\unicode[STIX]{x1D70E}}_{2}$
are in the same
$\widetilde{\unicode[STIX]{x1D70E}}_{2}$
are in the same
![]() $\ell$
-block of
$\ell$
-block of
![]() $\text{H}$
if and only if
$\text{H}$
if and only if
![]() $\widetilde{\unicode[STIX]{x1D70B}}_{1}$
and
$\widetilde{\unicode[STIX]{x1D70B}}_{1}$
and
![]() $\widetilde{\unicode[STIX]{x1D70B}}_{2}$
are in the same
$\widetilde{\unicode[STIX]{x1D70B}}_{2}$
are in the same
![]() $\ell$
-block of
$\ell$
-block of
![]() $\text{G}$
.
$\text{G}$
.
Proof. Proposition 6.1 implies that the
![]() $\ell$
-adic Jacquet–Langlands correspondence (6.2) induces a well-defined map from
$\ell$
-adic Jacquet–Langlands correspondence (6.2) induces a well-defined map from
![]() $\ell$
-blocks of discrete series representations of
$\ell$
-blocks of discrete series representations of
![]() $\text{H}$
to those of
$\text{H}$
to those of
![]() $\text{G}$
: given an
$\text{G}$
: given an
![]() $\ell$
-block of
$\ell$
-block of
![]() $\text{H}$
, if
$\text{H}$
, if
![]() $\widetilde{\unicode[STIX]{x1D70E}}$
is any
$\widetilde{\unicode[STIX]{x1D70E}}$
is any
![]() $\ell$
-adic discrete series representation in that block, then the
$\ell$
-adic discrete series representation in that block, then the
![]() $\ell$
-block of the transfer to
$\ell$
-block of the transfer to
![]() $\text{G}$
of
$\text{G}$
of
![]() $\widetilde{\unicode[STIX]{x1D70E}}$
is independent of the choice of
$\widetilde{\unicode[STIX]{x1D70E}}$
is independent of the choice of
![]() $\widetilde{\unicode[STIX]{x1D70E}}$
. This map also preserves depth so that, for any non-negative rational number
$\widetilde{\unicode[STIX]{x1D70E}}$
. This map also preserves depth so that, for any non-negative rational number
![]() $r\in \mathbf{Q}_{+}$
, we get a well-defined map from
$r\in \mathbf{Q}_{+}$
, we get a well-defined map from
![]() $\ell$
-blocks of discrete series representations of depth
$\ell$
-blocks of discrete series representations of depth
![]() $r$
of
$r$
of
![]() $\text{H}$
to
$\text{H}$
to
![]() $\ell$
-blocks of discrete series representations of depth
$\ell$
-blocks of discrete series representations of depth
![]() $r$
of
$r$
of
![]() $\text{G}$
. This map is between two finite sets of the same cardinality, since they are parametrized by the same objects: an endo-class of depth
$\text{G}$
. This map is between two finite sets of the same cardinality, since they are parametrized by the same objects: an endo-class of depth
![]() $r$
and, by Proposition 4.8, a parametrizing class up to reduction mod
$r$
and, by Proposition 4.8, a parametrizing class up to reduction mod
![]() $\ell$
. It is clearly surjective, and so is also injective.◻
$\ell$
. It is clearly surjective, and so is also injective.◻
Allowing
![]() $\ell$
to vary, we deduce the following result.
$\ell$
to vary, we deduce the following result.
Theorem 6.3. Two complex discrete series representations of
![]() $\text{G}$
are linked if and only if their transfers to
$\text{G}$
are linked if and only if their transfers to
![]() $\text{H}$
are linked.
$\text{H}$
are linked.
It follows that Proposition 5.8 (together with Remark 5.9) induces a map
depending on
![]() $\text{G}$
, where
$\text{G}$
, where
![]() $\mathscr{E}_{n}(\text{F})$
is the set of
$\mathscr{E}_{n}(\text{F})$
is the set of
![]() $\text{F}$
-endo-classes of degree dividing
$\text{F}$
-endo-classes of degree dividing
![]() $n$
. More precisely, given an endo-class
$n$
. More precisely, given an endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}\in \mathscr{E}_{n}(\text{F})$
and a complex discrete series representation
$\boldsymbol{\unicode[STIX]{x1D6E9}}\in \mathscr{E}_{n}(\text{F})$
and a complex discrete series representation
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $\text{G}$
of endo-class
$\text{G}$
of endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
, the endo-class of the Jacquet–Langlands transfer of
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
, the endo-class of the Jacquet–Langlands transfer of
![]() $\unicode[STIX]{x1D70B}$
to
$\unicode[STIX]{x1D70B}$
to
![]() $\text{H}$
depends only on
$\text{H}$
depends only on
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
: we denote it by
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
: we denote it by
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}_{1}(\boldsymbol{\unicode[STIX]{x1D6E9}})$
. This map does not depend on the choice of the isomorphisms
$\boldsymbol{\unicode[STIX]{x1D70B}}_{1}(\boldsymbol{\unicode[STIX]{x1D6E9}})$
. This map does not depend on the choice of the isomorphisms
![]() $\unicode[STIX]{x1D704}_{\ell }$
for
$\unicode[STIX]{x1D704}_{\ell }$
for
![]() $\ell$
dividing (5.1).
$\ell$
dividing (5.1).
Proposition 6.4. The map
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}_{1}$
is bijective.
$\boldsymbol{\unicode[STIX]{x1D70B}}_{1}$
is bijective.
Proof. This map is clearly surjective: given an endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}\in \mathscr{E}_{n}(\text{F})$
and any discrete series representation
$\boldsymbol{\unicode[STIX]{x1D6E9}}\in \mathscr{E}_{n}(\text{F})$
and any discrete series representation
![]() $\unicode[STIX]{x1D70E}\in \mathscr{D}(\text{H},\mathbf{C})$
with endo-class
$\unicode[STIX]{x1D70E}\in \mathscr{D}(\text{H},\mathbf{C})$
with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
, the endo-class of its inverse Jacquet–Langlands transfer
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
, the endo-class of its inverse Jacquet–Langlands transfer
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}^{-1}(\unicode[STIX]{x1D70E})\in \mathscr{D}(\text{G},\mathbf{C})$
is an antecedent of
$\boldsymbol{\unicode[STIX]{x1D70B}}^{-1}(\unicode[STIX]{x1D70E})\in \mathscr{D}(\text{G},\mathbf{C})$
is an antecedent of
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
by
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
by
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}_{1}$
.
$\boldsymbol{\unicode[STIX]{x1D70B}}_{1}$
.
Now let
![]() $\unicode[STIX]{x1D70B},\unicode[STIX]{x1D70B}\text{sp}\prime \in \mathscr{D}(\text{G},\mathbf{C})$
have Jacquet–Langlands transfers
$\unicode[STIX]{x1D70B},\unicode[STIX]{x1D70B}\text{sp}\prime \in \mathscr{D}(\text{G},\mathbf{C})$
have Jacquet–Langlands transfers
![]() $\unicode[STIX]{x1D70E}$
,
$\unicode[STIX]{x1D70E}$
,
![]() $\unicode[STIX]{x1D70E}\text{sp}\prime$
to
$\unicode[STIX]{x1D70E}\text{sp}\prime$
to
![]() $\text{H}$
with the same endo-class. By Proposition 5.8 and Remark 5.9, the representations
$\text{H}$
with the same endo-class. By Proposition 5.8 and Remark 5.9, the representations
![]() $\unicode[STIX]{x1D70E}$
,
$\unicode[STIX]{x1D70E}$
,
![]() $\unicode[STIX]{x1D70E}\text{sp}\prime$
are linked by a family of discrete series representations. By Theorem 6.3, the same holds for
$\unicode[STIX]{x1D70E}\text{sp}\prime$
are linked by a family of discrete series representations. By Theorem 6.3, the same holds for
![]() $\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}$
and
![]() $\unicode[STIX]{x1D70B}\text{sp}\prime$
. Thus they have the same endo-class.◻
$\unicode[STIX]{x1D70B}\text{sp}\prime$
. Thus they have the same endo-class.◻
Recall that the parametric degree of a cuspidal representation of
![]() $\text{G}$
has been defined in § 3.1.
$\text{G}$
has been defined in § 3.1.
Proposition 6.5. For every complex discrete series representation of
![]() $\text{G}$
, there is a cuspidal complex representation of
$\text{G}$
, there is a cuspidal complex representation of
![]() $\text{G}$
with the same endo-class and with parametric degree
$\text{G}$
with the same endo-class and with parametric degree
![]() $n$
.
$n$
.
Proof. Let
![]() $\unicode[STIX]{x1D70B}$
be a complex discrete series representation of
$\unicode[STIX]{x1D70B}$
be a complex discrete series representation of
![]() $\text{G}$
with endo-class
$\text{G}$
with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
. To find a complex cuspidal representation with the same endo-class and with parametric degree
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
. To find a complex cuspidal representation with the same endo-class and with parametric degree
![]() $n$
, we need to find a
$n$
, we need to find a
![]() $\text{Gal}(\boldsymbol{k}/\boldsymbol{d})$
-regular complex character
$\text{Gal}(\boldsymbol{k}/\boldsymbol{d})$
-regular complex character
![]() $\unicode[STIX]{x1D6FC}\in \text{X}$
which is also
$\unicode[STIX]{x1D6FC}\in \text{X}$
which is also
![]() $\text{Gal}(\boldsymbol{k}/\boldsymbol{e})$
-regular. The latter implies the former, so let us find a
$\text{Gal}(\boldsymbol{k}/\boldsymbol{e})$
-regular. The latter implies the former, so let us find a
![]() $\text{Gal}(\boldsymbol{k}/\boldsymbol{e})$
-regular character
$\text{Gal}(\boldsymbol{k}/\boldsymbol{e})$
-regular character
![]() $\unicode[STIX]{x1D6FC}\in \text{X}$
. For this, it is enough to choose for
$\unicode[STIX]{x1D6FC}\in \text{X}$
. For this, it is enough to choose for
![]() $\unicode[STIX]{x1D6FC}$
a generator of the cyclic group
$\unicode[STIX]{x1D6FC}$
a generator of the cyclic group
![]() $\text{X}$
.◻
$\text{X}$
.◻
As an immediate consequence we see that, given an endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
in
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
in
![]() $\mathscr{E}_{n}(\text{F})$
, if there is a single complex cuspidal representation
$\mathscr{E}_{n}(\text{F})$
, if there is a single complex cuspidal representation
![]() $\unicode[STIX]{x1D70C}$
of
$\unicode[STIX]{x1D70C}$
of
![]() $\text{G}$
with endo-class
$\text{G}$
with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
and parametric degree
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
and parametric degree
![]() $n$
such that
$n$
such that
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C})$
has endo-class
$\boldsymbol{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C})$
has endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
, then
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
, then
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}_{1}(\boldsymbol{\unicode[STIX]{x1D6E9}})$
is equal to
$\boldsymbol{\unicode[STIX]{x1D70B}}_{1}(\boldsymbol{\unicode[STIX]{x1D6E9}})$
is equal to
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
.
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
.
6.3
In this subsection the division algebra
![]() $\text{D}$
is fixed, but we allow the positive integer
$\text{D}$
is fixed, but we allow the positive integer
![]() $m$
to vary. Given an
$m$
to vary. Given an
![]() $m\geqslant 1$
, we write
$m\geqslant 1$
, we write
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}_{1,m}$
for the map (6.3) induced by the Jacquet–Langlands correspondence from
$\boldsymbol{\unicode[STIX]{x1D70B}}_{1,m}$
for the map (6.3) induced by the Jacquet–Langlands correspondence from
![]() $\mathscr{D}(\text{GL}_{m}(\text{D}),\mathbf{C})$
to
$\mathscr{D}(\text{GL}_{m}(\text{D}),\mathbf{C})$
to
![]() $\mathscr{D}(\text{GL}_{md}(\text{F}),\mathbf{C})$
. Recall (see Lemma 3.3) that associated with an endo-class
$\mathscr{D}(\text{GL}_{md}(\text{F}),\mathbf{C})$
. Recall (see Lemma 3.3) that associated with an endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}\in \mathscr{E}(\text{F})$
is an integer called its ramification index.
$\boldsymbol{\unicode[STIX]{x1D6E9}}\in \mathscr{E}(\text{F})$
is an integer called its ramification index.
Theorem 6.6.
![]() $(1)$
There is a unique map
$(1)$
There is a unique map
depending only on
![]() $\text{D}$
, such that for any integer
$\text{D}$
, such that for any integer
![]() $m\geqslant 1$
the restriction of
$m\geqslant 1$
the restriction of
![]() $\boldsymbol{j}$
to
$\boldsymbol{j}$
to
![]() $\mathscr{E}_{md}(\text{F})$
coincides with the map
$\mathscr{E}_{md}(\text{F})$
coincides with the map
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}_{1,m}$
.
$\boldsymbol{\unicode[STIX]{x1D70B}}_{1,m}$
.
![]() $(2)$
The map
$(2)$
The map
![]() $\boldsymbol{j}$
is bijective, and it is the identity on all essentially tame endo-classes (that is, all endo-classes whose ramification index is prime to
$\boldsymbol{j}$
is bijective, and it is the identity on all essentially tame endo-classes (that is, all endo-classes whose ramification index is prime to
![]() $p$
).
$p$
).
Proof. Uniqueness follows from the fact that
![]() $\mathscr{E}(\text{F})$
is the union of the
$\mathscr{E}(\text{F})$
is the union of the
![]() $\mathscr{E}_{md}(\text{F})$
for
$\mathscr{E}_{md}(\text{F})$
for
![]() $m\geqslant 1$
.
$m\geqslant 1$
.
In order to prove the existence of
![]() $\boldsymbol{j}$
, it suffices to prove that for all
$\boldsymbol{j}$
, it suffices to prove that for all
![]() $m,k\geqslant 1$
, the maps
$m,k\geqslant 1$
, the maps
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}_{1,m}$
and
$\boldsymbol{\unicode[STIX]{x1D70B}}_{1,m}$
and
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}_{1,k}$
coincide on
$\boldsymbol{\unicode[STIX]{x1D70B}}_{1,k}$
coincide on
![]() $\mathscr{E}_{md}(\text{F})\,\cap \,\mathscr{E}_{kd}(\text{F})=\mathscr{E}_{rd}(\text{F})$
, where
$\mathscr{E}_{md}(\text{F})\,\cap \,\mathscr{E}_{kd}(\text{F})=\mathscr{E}_{rd}(\text{F})$
, where
![]() $r$
denotes the greatest common divisor of
$r$
denotes the greatest common divisor of
![]() $m$
and
$m$
and
![]() $k$
. For this, let
$k$
. For this, let
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}\in \mathscr{E}_{rd}(\text{F})$
, and let
$\boldsymbol{\unicode[STIX]{x1D6E9}}\in \mathscr{E}_{rd}(\text{F})$
, and let
![]() $\unicode[STIX]{x1D70C}$
be a cuspidal irreducible representation of
$\unicode[STIX]{x1D70C}$
be a cuspidal irreducible representation of
![]() $\text{GL}_{r}(\text{D})$
with endo-class
$\text{GL}_{r}(\text{D})$
with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
and parametric degree
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
and parametric degree
![]() $rd$
. Its Jacquet–Langlands transfer to
$rd$
. Its Jacquet–Langlands transfer to
![]() $\text{GL}_{rd}(\text{F})$
is a cuspidal representation
$\text{GL}_{rd}(\text{F})$
is a cuspidal representation
![]() $\unicode[STIX]{x1D70E}$
, whose endo-class is denoted by
$\unicode[STIX]{x1D70E}$
, whose endo-class is denoted by
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}\text{sp}\prime$
. Then, for any
$\boldsymbol{\unicode[STIX]{x1D6E9}}\text{sp}\prime$
. Then, for any
![]() $a\geqslant 1$
, the discrete series representation
$a\geqslant 1$
, the discrete series representation
![]() $\text{L}(\unicode[STIX]{x1D70C},a)$
of
$\text{L}(\unicode[STIX]{x1D70C},a)$
of
![]() $\text{GL}_{ar}(\text{D})$
has endo-class
$\text{GL}_{ar}(\text{D})$
has endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
, and its transfer
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
, and its transfer
![]() $\text{L}(\unicode[STIX]{x1D70E},a)$
to
$\text{L}(\unicode[STIX]{x1D70E},a)$
to
![]() $\text{GL}_{ard}(\text{F})$
has endo-class
$\text{GL}_{ard}(\text{F})$
has endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}\text{sp}\prime$
. It follows that
$\boldsymbol{\unicode[STIX]{x1D6E9}}\text{sp}\prime$
. It follows that
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}_{1,m}(\boldsymbol{\unicode[STIX]{x1D6E9}})=\boldsymbol{\unicode[STIX]{x1D70B}}_{1,r}(\boldsymbol{\unicode[STIX]{x1D6E9}})=\boldsymbol{\unicode[STIX]{x1D6E9}}\text{sp}\prime$
. The bijectivity of
$\boldsymbol{\unicode[STIX]{x1D70B}}_{1,m}(\boldsymbol{\unicode[STIX]{x1D6E9}})=\boldsymbol{\unicode[STIX]{x1D70B}}_{1,r}(\boldsymbol{\unicode[STIX]{x1D6E9}})=\boldsymbol{\unicode[STIX]{x1D6E9}}\text{sp}\prime$
. The bijectivity of
![]() $\boldsymbol{j}$
follows from the fact that all the maps
$\boldsymbol{j}$
follows from the fact that all the maps
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}_{1,m}$
, for
$\boldsymbol{\unicode[STIX]{x1D70B}}_{1,m}$
, for
![]() $m\geqslant 1$
, are bijective.
$m\geqslant 1$
, are bijective.
To prove the second part of statement (2), given an essentially tame endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
, it suffices to find a single complex cuspidal representation
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
, it suffices to find a single complex cuspidal representation
![]() $\unicode[STIX]{x1D70C}$
of
$\unicode[STIX]{x1D70C}$
of
![]() $\text{G}$
with endo-class
$\text{G}$
with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
and parametric degree
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
and parametric degree
![]() $n$
such that
$n$
such that
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C})$
has endo-class
$\boldsymbol{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C})$
has endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
. But it follows from [Reference Bushnell and HenniartBH11a], which gives an explicit type-theoretic description of the Jacquet–Langlands transfer of complex cuspidal representations of
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
. But it follows from [Reference Bushnell and HenniartBH11a], which gives an explicit type-theoretic description of the Jacquet–Langlands transfer of complex cuspidal representations of
![]() $\text{G}$
with essentially tame endo-class and parametric degree
$\text{G}$
with essentially tame endo-class and parametric degree
![]() $n$
, that this is true of any complex cuspidal representation
$n$
, that this is true of any complex cuspidal representation
![]() $\unicode[STIX]{x1D70C}$
of
$\unicode[STIX]{x1D70C}$
of
![]() $\text{G}$
with endo-class
$\text{G}$
with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
and parametric degree
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
and parametric degree
![]() $n$
.◻
$n$
.◻
Remark 6.7. After this paper was written, Dotto proved the Endo-class Invariance Conjecture in [Reference DottoDot17]. Thus it is now known that the map
![]() $\boldsymbol{j}$
of Theorem 6.6 is in fact the identity.
$\boldsymbol{j}$
of Theorem 6.6 is in fact the identity.
7 Reduction to the maximal totally ramified case
We continue with the previous notation, so that
![]() $\text{G}=\text{GL}_{m}(\text{D})$
and
$\text{G}=\text{GL}_{m}(\text{D})$
and
![]() $\text{H}=\text{GL}_{n}(\text{F})$
. In this section, we closely follow the ideas of [Reference Bushnell and HenniartBH11a, § 6] to make a further reduction to the maximal totally ramified case (see § 1.1). All representations in this section are complex.
$\text{H}=\text{GL}_{n}(\text{F})$
. In this section, we closely follow the ideas of [Reference Bushnell and HenniartBH11a, § 6] to make a further reduction to the maximal totally ramified case (see § 1.1). All representations in this section are complex.
7.1
Let
![]() $\unicode[STIX]{x1D70B}$
be a cuspidal (complex) representation of
$\unicode[STIX]{x1D70B}$
be a cuspidal (complex) representation of
![]() $\text{G}$
with parametric degree
$\text{G}$
with parametric degree
![]() $n$
. Let
$n$
. Let
![]() $(\mathbf{\text{J}},\boldsymbol{\unicode[STIX]{x1D706}})$
be an extended maximal simple type of
$(\mathbf{\text{J}},\boldsymbol{\unicode[STIX]{x1D706}})$
be an extended maximal simple type of
![]() $\text{G}$
contained in
$\text{G}$
contained in
![]() $\unicode[STIX]{x1D70B}$
[Reference Mínguez and SécherreMS14b, § 3.1 and Théorème 3.11], attached to a simple stratum
$\unicode[STIX]{x1D70B}$
[Reference Mínguez and SécherreMS14b, § 3.1 and Théorème 3.11], attached to a simple stratum
![]() $[\mathfrak{a},\unicode[STIX]{x1D6FD}]$
and a simple character
$[\mathfrak{a},\unicode[STIX]{x1D6FD}]$
and a simple character
![]() $\unicode[STIX]{x1D703}\in \mathscr{C}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
. Write
$\unicode[STIX]{x1D703}\in \mathscr{C}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
. Write
![]() $\text{B}$
for the centralizer of
$\text{B}$
for the centralizer of
![]() $\unicode[STIX]{x1D6FD}$
in
$\unicode[STIX]{x1D6FD}$
in
![]() $\text{M}_{m}(\text{D})$
, so that
$\text{M}_{m}(\text{D})$
, so that
![]() $\text{B}\simeq \text{M}_{m\text{sp}\prime }(\text{D}\text{sp}\prime )$
for some integer
$\text{B}\simeq \text{M}_{m\text{sp}\prime }(\text{D}\text{sp}\prime )$
for some integer
![]() $m\text{sp}\prime \geqslant 1$
and
$m\text{sp}\prime \geqslant 1$
and
![]() $\text{F}[\unicode[STIX]{x1D6FD}]$
-division algebra
$\text{F}[\unicode[STIX]{x1D6FD}]$
-division algebra
![]() $\text{D}\text{sp}\prime$
. Fix a maximal unramified extension
$\text{D}\text{sp}\prime$
. Fix a maximal unramified extension
![]() $\text{L}$
of
$\text{L}$
of
![]() $\text{F}[\unicode[STIX]{x1D6FD}]$
in
$\text{F}[\unicode[STIX]{x1D6FD}]$
in
![]() $\text{B}$
, and write
$\text{B}$
, and write
![]() $\text{K}$
for the maximal unramified subextension of
$\text{K}$
for the maximal unramified subextension of
![]() $\text{L}$
over
$\text{L}$
over
![]() $\text{F}$
.
$\text{F}$
.
We fix a root of unity
![]() $\unicode[STIX]{x1D701}\in \text{K}$
of order relatively prime to
$\unicode[STIX]{x1D701}\in \text{K}$
of order relatively prime to
![]() $p$
such that
$p$
such that
![]() $\text{K}=\text{F}[\unicode[STIX]{x1D701}]$
. Write
$\text{K}=\text{F}[\unicode[STIX]{x1D701}]$
. Write
![]() $\text{G}_{\text{K}}$
for the centralizer of
$\text{G}_{\text{K}}$
for the centralizer of
![]() $\text{K}$
in
$\text{K}$
in
![]() $\text{G}$
. Let
$\text{G}$
. Let
![]() $u$
be a pro-unipotent, elliptic regular element of
$u$
be a pro-unipotent, elliptic regular element of
![]() $\text{G}_{\text{K}}$
in the sense of [Reference Bushnell and HenniartBH11a, § 1.6]. The element
$\text{G}_{\text{K}}$
in the sense of [Reference Bushnell and HenniartBH11a, § 1.6]. The element
![]() $h=\unicode[STIX]{x1D701}u$
then lies in the set
$h=\unicode[STIX]{x1D701}u$
then lies in the set
![]() $\text{G}_{\text{reg}}^{\text{ell}}$
of elliptic regular elements of
$\text{G}_{\text{reg}}^{\text{ell}}$
of elliptic regular elements of
![]() $\text{G}$
, so we have
$\text{G}$
, so we have
as in [Reference Bushnell and HenniartBH11a, (6.3.1)]. Write
![]() $\text{J}=\text{J}(\mathfrak{a},\unicode[STIX]{x1D6FD})=\mathbf{\text{J}}\,\cap \,\mathfrak{a}^{\times }$
. A coset
$\text{J}=\text{J}(\mathfrak{a},\unicode[STIX]{x1D6FD})=\mathbf{\text{J}}\,\cap \,\mathfrak{a}^{\times }$
. A coset
![]() $x\mathbf{\text{J}}$
can contribute to the sum only if
$x\mathbf{\text{J}}$
can contribute to the sum only if
![]() $x^{-1}hx\in \mathbf{\text{J}}$
or, equivalently,
$x^{-1}hx\in \mathbf{\text{J}}$
or, equivalently,
![]() $x^{-1}hx\in \text{J}$
. As in [Reference Bushnell and HenniartBH11a, 6.3 Lemma], such a coset
$x^{-1}hx\in \text{J}$
. As in [Reference Bushnell and HenniartBH11a, 6.3 Lemma], such a coset
![]() $x\mathbf{\text{J}}$
is contained in
$x\mathbf{\text{J}}$
is contained in
![]() $\text{N}_{\text{G}}(\text{K})\mathbf{\text{J}}$
, where
$\text{N}_{\text{G}}(\text{K})\mathbf{\text{J}}$
, where
![]() $\text{N}_{\text{G}}(\text{K})$
is the normalizer of
$\text{N}_{\text{G}}(\text{K})$
is the normalizer of
![]() $\text{K}$
in
$\text{K}$
in
![]() $\text{G}$
.
$\text{G}$
.
Write
![]() $\unicode[STIX]{x1D6F9}$
for the Galois group of
$\unicode[STIX]{x1D6F9}$
for the Galois group of
![]() $\text{K}/\text{F}$
and
$\text{K}/\text{F}$
and
![]() $\unicode[STIX]{x1D6E4}$
for that of
$\unicode[STIX]{x1D6E4}$
for that of
![]() $\text{L}/\text{F}[\unicode[STIX]{x1D6FD}]$
. Restriction of operators identifies
$\text{L}/\text{F}[\unicode[STIX]{x1D6FD}]$
. Restriction of operators identifies
![]() $\unicode[STIX]{x1D6E4}$
with a subgroup of
$\unicode[STIX]{x1D6E4}$
with a subgroup of
![]() $\unicode[STIX]{x1D6F9}$
. Write
$\unicode[STIX]{x1D6F9}$
. Write
![]() $\unicode[STIX]{x1D6F9}_{\text{t}}$
for the unique subgroup of
$\unicode[STIX]{x1D6F9}_{\text{t}}$
for the unique subgroup of
![]() $\unicode[STIX]{x1D6E4}$
(and hence of
$\unicode[STIX]{x1D6E4}$
(and hence of
![]() $\unicode[STIX]{x1D6F9}$
) of order
$\unicode[STIX]{x1D6F9}$
) of order
![]() $m\text{sp}\prime s(\unicode[STIX]{x1D70B})$
, where
$m\text{sp}\prime s(\unicode[STIX]{x1D70B})$
, where
![]() $s(\unicode[STIX]{x1D70B})$
is the integer introduced in § 3.1. Thanks to the description of the group
$s(\unicode[STIX]{x1D70B})$
is the integer introduced in § 3.1. Thanks to the description of the group
![]() $\mathbf{\text{J}}$
in [Reference SécherreSéc05b, 5.1], we observe that
$\mathbf{\text{J}}$
in [Reference SécherreSéc05b, 5.1], we observe that
![]() $\unicode[STIX]{x1D6F9}_{\text{t}}$
is the image of
$\unicode[STIX]{x1D6F9}_{\text{t}}$
is the image of
![]() $\mathbf{\text{J}}\,\cap \,\text{N}_{\text{G}}(\text{K})$
under the surjective map
$\mathbf{\text{J}}\,\cap \,\text{N}_{\text{G}}(\text{K})$
under the surjective map
![]() $\text{N}_{\text{G}}(\text{K})/\text{G}_{\text{K}}\rightarrow \unicode[STIX]{x1D6F9}$
. As in [Reference Bushnell and HenniartBH11a, (6.3.2)], we have
$\text{N}_{\text{G}}(\text{K})/\text{G}_{\text{K}}\rightarrow \unicode[STIX]{x1D6F9}$
. As in [Reference Bushnell and HenniartBH11a, (6.3.2)], we have
where
![]() $\mathbf{\text{J}}_{\text{K}}=\mathbf{\text{J}}\,\cap \,\text{G}_{\text{K}}$
.
$\mathbf{\text{J}}_{\text{K}}=\mathbf{\text{J}}\,\cap \,\text{G}_{\text{K}}$
.
Let us fix a uniformizer
![]() $\unicode[STIX]{x1D71B}_{\text{F}}$
of
$\unicode[STIX]{x1D71B}_{\text{F}}$
of
![]() $\text{F}$
. We choose an irreducible representation
$\text{F}$
. We choose an irreducible representation
![]() $\boldsymbol{\unicode[STIX]{x1D705}}$
of
$\boldsymbol{\unicode[STIX]{x1D705}}$
of
![]() $\mathbf{\text{J}}$
such that:
$\mathbf{\text{J}}$
such that:
(1) the restriction of
 $\boldsymbol{\unicode[STIX]{x1D705}}$
to
$\boldsymbol{\unicode[STIX]{x1D705}}$
to
 $\text{J}$
is a
$\text{J}$
is a
 $\unicode[STIX]{x1D6FD}$
-extension of
$\unicode[STIX]{x1D6FD}$
-extension of
 $\unicode[STIX]{x1D703}$
;
$\unicode[STIX]{x1D703}$
;(2) the character
 $\det (\boldsymbol{\unicode[STIX]{x1D705}})$
has order a power of
$\det (\boldsymbol{\unicode[STIX]{x1D705}})$
has order a power of
 $p$
;
$p$
;(3) the automorphism
 $\boldsymbol{\unicode[STIX]{x1D705}}(\unicode[STIX]{x1D71B}_{\text{F}})$
is the identity.
$\boldsymbol{\unicode[STIX]{x1D705}}(\unicode[STIX]{x1D71B}_{\text{F}})$
is the identity.
Note that such a representation is not unique. We now write
which carries an action of
![]() $\mathbf{\text{J}}$
given by
$\mathbf{\text{J}}$
given by
![]() $g\cdot f=\boldsymbol{\unicode[STIX]{x1D706}}(g)\circ f\circ \boldsymbol{\unicode[STIX]{x1D705}}(g)^{-1}$
for
$g\cdot f=\boldsymbol{\unicode[STIX]{x1D706}}(g)\circ f\circ \boldsymbol{\unicode[STIX]{x1D705}}(g)^{-1}$
for
![]() $g\in \mathbf{\text{J}}$
and
$g\in \mathbf{\text{J}}$
and
![]() $f\in \boldsymbol{\unicode[STIX]{x1D70E}}$
. This representation is irreducible and trivial on
$f\in \boldsymbol{\unicode[STIX]{x1D70E}}$
. This representation is irreducible and trivial on
![]() $\text{J}^{1}=\text{J}^{1}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
, and we have the decomposition
$\text{J}^{1}=\text{J}^{1}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
, and we have the decomposition
![]() $\boldsymbol{\unicode[STIX]{x1D706}}=\boldsymbol{\unicode[STIX]{x1D705}}\,\otimes \,\boldsymbol{\unicode[STIX]{x1D70E}}$
. As in [Reference Bushnell and HenniartBH11a, (6.4.1)], this gives
$\boldsymbol{\unicode[STIX]{x1D706}}=\boldsymbol{\unicode[STIX]{x1D705}}\,\otimes \,\boldsymbol{\unicode[STIX]{x1D70E}}$
. As in [Reference Bushnell and HenniartBH11a, (6.4.1)], this gives
We are now going to interpret the sum over
![]() $\text{G}_{\text{K}}/\mathbf{\text{J}}_{\text{K}}$
as the trace of a cuspidal irreducible representation of
$\text{G}_{\text{K}}/\mathbf{\text{J}}_{\text{K}}$
as the trace of a cuspidal irreducible representation of
![]() $\text{G}_{\text{K}}$
.
$\text{G}_{\text{K}}$
.
7.2
Write
![]() $\unicode[STIX]{x1D703}_{\text{K}}$
for the restriction of
$\unicode[STIX]{x1D703}_{\text{K}}$
for the restriction of
![]() $\unicode[STIX]{x1D703}$
to
$\unicode[STIX]{x1D703}$
to
![]() $\text{H}^{1}(\mathfrak{a},\unicode[STIX]{x1D6FD})\,\cap \,\text{G}_{\text{K}}$
, which is the interior
$\text{H}^{1}(\mathfrak{a},\unicode[STIX]{x1D6FD})\,\cap \,\text{G}_{\text{K}}$
, which is the interior
![]() $\text{K}/\text{F}$
-lift of the simple character
$\text{K}/\text{F}$
-lift of the simple character
![]() $\unicode[STIX]{x1D703}$
in the sense of [Reference Broussous, Sécherre and StevensBSS12, § 5]. The group
$\unicode[STIX]{x1D703}$
in the sense of [Reference Broussous, Sécherre and StevensBSS12, § 5]. The group
![]() $\mathbf{\text{J}}_{\text{K}}$
is also the normalizer of
$\mathbf{\text{J}}_{\text{K}}$
is also the normalizer of
![]() $\unicode[STIX]{x1D703}_{\text{K}}$
in
$\unicode[STIX]{x1D703}_{\text{K}}$
in
![]() $\text{G}_{\text{K}}$
. We choose an irreducible representation
$\text{G}_{\text{K}}$
. We choose an irreducible representation
![]() $\boldsymbol{\unicode[STIX]{x1D705}}_{\text{K}}$
of
$\boldsymbol{\unicode[STIX]{x1D705}}_{\text{K}}$
of
![]() $\mathbf{\text{J}}_{\text{K}}$
such that:
$\mathbf{\text{J}}_{\text{K}}$
such that:
(1) the restriction of
 $\boldsymbol{\unicode[STIX]{x1D705}}_{\text{K}}$
to
$\boldsymbol{\unicode[STIX]{x1D705}}_{\text{K}}$
to
 $\text{J}_{\text{K}}$
is a
$\text{J}_{\text{K}}$
is a
 $\unicode[STIX]{x1D6FD}$
-extension of
$\unicode[STIX]{x1D6FD}$
-extension of
 $\unicode[STIX]{x1D703}_{\text{K}}$
;
$\unicode[STIX]{x1D703}_{\text{K}}$
;(2) the character
 $\det (\boldsymbol{\unicode[STIX]{x1D705}}_{\text{K}})$
has order a power of
$\det (\boldsymbol{\unicode[STIX]{x1D705}}_{\text{K}})$
has order a power of
 $p$
;
$p$
;(3) the automorphism
 $\boldsymbol{\unicode[STIX]{x1D705}}_{\text{K}}(\unicode[STIX]{x1D71B}_{\text{F}})$
is the identity.
$\boldsymbol{\unicode[STIX]{x1D705}}_{\text{K}}(\unicode[STIX]{x1D71B}_{\text{F}})$
is the identity.
Again, such a choice may not be unique. The pair
![]() $(\mathbf{\text{J}}_{\text{K}},\boldsymbol{\unicode[STIX]{x1D705}}_{\text{K}})$
is an extended maximal simple type in
$(\mathbf{\text{J}}_{\text{K}},\boldsymbol{\unicode[STIX]{x1D705}}_{\text{K}})$
is an extended maximal simple type in
![]() $\text{G}_{\text{K}}$
. It thus defines a cuspidal irreducible representation
$\text{G}_{\text{K}}$
. It thus defines a cuspidal irreducible representation
![]() $\unicode[STIX]{x1D70C}$
of
$\unicode[STIX]{x1D70C}$
of
![]() $\text{G}_{\text{K}}$
. By [Reference Bushnell and HenniartBH10, (3.4.3) and (5.6.2)], there is a sign
$\text{G}_{\text{K}}$
. By [Reference Bushnell and HenniartBH10, (3.4.3) and (5.6.2)], there is a sign
![]() $\unicode[STIX]{x1D716}\in \{-1,+1\}$
such that
$\unicode[STIX]{x1D716}\in \{-1,+1\}$
such that
As in [Reference Bushnell and HenniartBH11a, (6.4.2)], this gives
We do not know whether a result similar to [Reference Bushnell and HenniartBH11a, 6.5 Lemma] holds, that is, we do not know whether the
![]() $\unicode[STIX]{x1D6F9}$
-stabilizers of
$\unicode[STIX]{x1D6F9}$
-stabilizers of
![]() $\unicode[STIX]{x1D70C}$
and of its inertial class are both equal to
$\unicode[STIX]{x1D70C}$
and of its inertial class are both equal to
![]() $\unicode[STIX]{x1D6E4}$
. However, let
$\unicode[STIX]{x1D6E4}$
. However, let
![]() $\unicode[STIX]{x1D6F9}_{0}$
denote the stabilizer in
$\unicode[STIX]{x1D6F9}_{0}$
denote the stabilizer in
![]() $\unicode[STIX]{x1D6F9}$
of the inertial class of
$\unicode[STIX]{x1D6F9}$
of the inertial class of
![]() $\unicode[STIX]{x1D70C}$
and let
$\unicode[STIX]{x1D70C}$
and let
![]() $\text{X}_{0}$
be a set of representatives for
$\text{X}_{0}$
be a set of representatives for
![]() $\unicode[STIX]{x1D6F9}$
mod
$\unicode[STIX]{x1D6F9}$
mod
![]() $\unicode[STIX]{x1D6F9}_{0}$
. For
$\unicode[STIX]{x1D6F9}_{0}$
. For
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6F9}_{0}$
there is an unramified character
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6F9}_{0}$
there is an unramified character
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FE}}$
of
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FE}}$
of
![]() $\text{G}_{\text{K}}$
such that
$\text{G}_{\text{K}}$
such that
![]() $\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D6FE}^{-1}}\simeq \unicode[STIX]{x1D70C}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FE}}$
. Since
$\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D6FE}^{-1}}\simeq \unicode[STIX]{x1D70C}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FE}}$
. Since
![]() $u$
is pro-unipotent (and hence compact), we have
$u$
is pro-unipotent (and hence compact), we have
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FC}^{-1}}(u)=1$
for all
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FC}^{-1}}(u)=1$
for all
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F9}/\unicode[STIX]{x1D6F9}_{\text{t}}$
. Therefore (7.1) can be rewritten as
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F9}/\unicode[STIX]{x1D6F9}_{\text{t}}$
. Therefore (7.1) can be rewritten as
Note that the map
is not identically zero on the set of
![]() $\text{K}/\text{F}$
-regular roots of unity, by [Reference Silberger and ZinkSZ00, Theorem 1.1(ii)]. Thus there is an
$\text{K}/\text{F}$
-regular roots of unity, by [Reference Silberger and ZinkSZ00, Theorem 1.1(ii)]. Thus there is an
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F9}$
such that the coefficient
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F9}$
such that the coefficient
![]() $w(\unicode[STIX]{x1D701}^{\unicode[STIX]{x1D6FC}})$
in (7.2) is nonzero.
$w(\unicode[STIX]{x1D701}^{\unicode[STIX]{x1D6FC}})$
in (7.2) is nonzero.
7.3
Now write
![]() $\unicode[STIX]{x1D70B}\text{sp}\prime$
for the Jacquet–Langlands transfer of
$\unicode[STIX]{x1D70B}\text{sp}\prime$
for the Jacquet–Langlands transfer of
![]() $\unicode[STIX]{x1D70B}$
to
$\unicode[STIX]{x1D70B}$
to
![]() $\text{H}$
. Since
$\text{H}$
. Since
![]() $\unicode[STIX]{x1D70B}$
has parametric degree
$\unicode[STIX]{x1D70B}$
has parametric degree
![]() $n$
, the torsion number
$n$
, the torsion number
![]() $t(\unicode[STIX]{x1D70B})$
is equal to the degree of
$t(\unicode[STIX]{x1D70B})$
is equal to the degree of
![]() $\text{K}$
over
$\text{K}$
over
![]() $\text{F}$
. We now do for
$\text{F}$
. We now do for
![]() $\unicode[STIX]{x1D70B}\text{sp}\prime$
what we did for
$\unicode[STIX]{x1D70B}\text{sp}\prime$
what we did for
![]() $\unicode[STIX]{x1D70B}$
.
$\unicode[STIX]{x1D70B}$
.
Let
![]() $(\mathbf{\text{J}}\text{sp}\prime ,\boldsymbol{\unicode[STIX]{x1D706}}\text{sp}\prime )$
be an extended maximal simple type of
$(\mathbf{\text{J}}\text{sp}\prime ,\boldsymbol{\unicode[STIX]{x1D706}}\text{sp}\prime )$
be an extended maximal simple type of
![]() $\text{H}$
contained in
$\text{H}$
contained in
![]() $\unicode[STIX]{x1D70B}\text{sp}\prime$
, attached to a simple stratum
$\unicode[STIX]{x1D70B}\text{sp}\prime$
, attached to a simple stratum
![]() $[\mathfrak{a}\text{sp}\prime ,\unicode[STIX]{x1D6FD}\text{sp}\prime ]$
. Write
$[\mathfrak{a}\text{sp}\prime ,\unicode[STIX]{x1D6FD}\text{sp}\prime ]$
. Write
![]() $\text{B}\text{sp}\prime$
for the centralizer of
$\text{B}\text{sp}\prime$
for the centralizer of
![]() $\unicode[STIX]{x1D6FD}\text{sp}\prime$
in
$\unicode[STIX]{x1D6FD}\text{sp}\prime$
in
![]() $\text{M}_{n}(\text{F})$
, fix a maximal unramified extension
$\text{M}_{n}(\text{F})$
, fix a maximal unramified extension
![]() $\text{L}\text{sp}\prime$
of
$\text{L}\text{sp}\prime$
of
![]() $\text{F}[\unicode[STIX]{x1D6FD}\text{sp}\prime ]$
in
$\text{F}[\unicode[STIX]{x1D6FD}\text{sp}\prime ]$
in
![]() $\text{B}\text{sp}\prime$
and write
$\text{B}\text{sp}\prime$
and write
![]() $\text{K}\text{sp}\prime$
for the maximal unramified subextension of
$\text{K}\text{sp}\prime$
for the maximal unramified subextension of
![]() $\text{L}\text{sp}\prime$
over
$\text{L}\text{sp}\prime$
over
![]() $\text{F}$
. The relation
$\text{F}$
. The relation
![]() $t(\unicode[STIX]{x1D70B})=t(\unicode[STIX]{x1D70B}\text{sp}\prime )$
, together with the fact that
$t(\unicode[STIX]{x1D70B})=t(\unicode[STIX]{x1D70B}\text{sp}\prime )$
, together with the fact that
![]() $\unicode[STIX]{x1D70B}\text{sp}\prime$
also has parametric degree
$\unicode[STIX]{x1D70B}\text{sp}\prime$
also has parametric degree
![]() $n$
, implies that
$n$
, implies that
![]() $\text{K}\text{sp}\prime$
and
$\text{K}\text{sp}\prime$
and
![]() $\text{K}$
have the same degree over
$\text{K}$
have the same degree over
![]() $\text{F}$
. Therefore, we may identify the maximal unramified subextension of
$\text{F}$
. Therefore, we may identify the maximal unramified subextension of
![]() $\text{L}\text{sp}\prime /\text{F}$
with
$\text{L}\text{sp}\prime /\text{F}$
with
![]() $\text{K}$
.
$\text{K}$
.
We have an analogue
![]() $\boldsymbol{\unicode[STIX]{x1D70E}}\text{sp}\prime$
of
$\boldsymbol{\unicode[STIX]{x1D70E}}\text{sp}\prime$
of
![]() $\boldsymbol{\unicode[STIX]{x1D70E}}$
and an analogue
$\boldsymbol{\unicode[STIX]{x1D70E}}$
and an analogue
![]() $\unicode[STIX]{x1D70C}\text{sp}\prime$
of
$\unicode[STIX]{x1D70C}\text{sp}\prime$
of
![]() $\unicode[STIX]{x1D70C}$
in the argument of the previous subsection, so that we get
$\unicode[STIX]{x1D70C}$
in the argument of the previous subsection, so that we get
where
![]() $\unicode[STIX]{x1D701}\in \text{K}$
is as above,
$\unicode[STIX]{x1D701}\in \text{K}$
is as above,
![]() $u\text{sp}\prime$
is a pro-unipotent elliptic regular element of the centralizer
$u\text{sp}\prime$
is a pro-unipotent elliptic regular element of the centralizer
![]() $\text{H}_{\text{K}}$
of
$\text{H}_{\text{K}}$
of
![]() $\text{K}$
in
$\text{K}$
in
![]() $\text{H}$
,
$\text{H}$
,
![]() $\unicode[STIX]{x1D716}\text{sp}\prime \in \{-1,+1\}$
is a sign, and the subgroups
$\unicode[STIX]{x1D716}\text{sp}\prime \in \{-1,+1\}$
is a sign, and the subgroups
![]() $\unicode[STIX]{x1D6F9}_{\text{t}}^{\prime }$
,
$\unicode[STIX]{x1D6F9}_{\text{t}}^{\prime }$
,
![]() $\unicode[STIX]{x1D6F9}\text{sp}\prime _{0}$
and
$\unicode[STIX]{x1D6F9}\text{sp}\prime _{0}$
and
![]() $\text{X}_{0}^{\prime }$
are defined as in the previous subsection. If
$\text{X}_{0}^{\prime }$
are defined as in the previous subsection. If
![]() $\unicode[STIX]{x1D701}u\text{sp}\prime$
is chosen to have the same reduced characteristic polynomial over
$\unicode[STIX]{x1D701}u\text{sp}\prime$
is chosen to have the same reduced characteristic polynomial over
![]() $\text{F}$
as
$\text{F}$
as
![]() $\unicode[STIX]{x1D701}u$
, this is equal to
$\unicode[STIX]{x1D701}u$
, this is equal to
![]() $(-1)^{n-m}\cdot \text{tr}\,\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D701}u)$
, by the trace relation characterizing the Jacquet–Langlands correspondence. We thus get
$(-1)^{n-m}\cdot \text{tr}\,\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D701}u)$
, by the trace relation characterizing the Jacquet–Langlands correspondence. We thus get
where the function
![]() $w$
and its analogue
$w$
and its analogue
![]() $w\text{sp}\prime$
are defined by (7.3).
$w\text{sp}\prime$
are defined by (7.3).
We apply [Reference Bushnell and HenniartBH11a, 6.6 Lemma] (note that
![]() $\unicode[STIX]{x1D70C}$
has maximal parametric degree since
$\unicode[STIX]{x1D70C}$
has maximal parametric degree since
![]() $\text{L}/\text{K}$
is maximal). The
$\text{L}/\text{K}$
is maximal). The
![]() $\unicode[STIX]{x1D70C}\text{sp}\prime ^{\unicode[STIX]{x1D6FC}\text{sp}\prime ^{-1}}$
,
$\unicode[STIX]{x1D70C}\text{sp}\prime ^{\unicode[STIX]{x1D6FC}\text{sp}\prime ^{-1}}$
,
![]() $\unicode[STIX]{x1D6FC}\text{sp}\prime \in \text{X}\text{sp}\prime _{0}$
, are not unramified twists of each other, and the same holds for the Jacquet–Langlands transfers to
$\unicode[STIX]{x1D6FC}\text{sp}\prime \in \text{X}\text{sp}\prime _{0}$
, are not unramified twists of each other, and the same holds for the Jacquet–Langlands transfers to
![]() $\text{H}_{\text{K}}$
of the
$\text{H}_{\text{K}}$
of the
![]() $\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D6FC}^{-1}}$
,
$\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D6FC}^{-1}}$
,
![]() $\unicode[STIX]{x1D6FC}\in \text{X}_{0}$
. Thanks to the linear independence of characters, it follows that there is an
$\unicode[STIX]{x1D6FC}\in \text{X}_{0}$
. Thanks to the linear independence of characters, it follows that there is an
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F9}$
such that
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F9}$
such that
for some unramified character
![]() $\unicode[STIX]{x1D712}$
of
$\unicode[STIX]{x1D712}$
of
![]() $\text{H}_{\text{K}}$
, where
$\text{H}_{\text{K}}$
, where
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}_{\text{K}}$
is the local Jacquet–Langlands correspondence from
$\boldsymbol{\unicode[STIX]{x1D70B}}_{\text{K}}$
is the local Jacquet–Langlands correspondence from
![]() $\text{G}_{\text{K}}$
to
$\text{G}_{\text{K}}$
to
![]() $\text{H}_{\text{K}}$
.
$\text{H}_{\text{K}}$
.
Assume now that
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}_{\text{K}}$
preserves
$\boldsymbol{\unicode[STIX]{x1D70B}}_{\text{K}}$
preserves
![]() $\text{K}$
-endo-classes for maximal totally ramified cuspidal representations of
$\text{K}$
-endo-classes for maximal totally ramified cuspidal representations of
![]() $\text{G}_{\text{K}}$
. Write
$\text{G}_{\text{K}}$
. Write
![]() $\mathscr{E}(\text{F})$
for the set of endo-classes over
$\mathscr{E}(\text{F})$
for the set of endo-classes over
![]() $\text{F}$
, and likewise
$\text{F}$
, and likewise
![]() $\mathscr{E}(\text{K})$
. The representations
$\mathscr{E}(\text{K})$
. The representations
![]() $\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D6FC}^{-1}}$
and
$\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D6FC}^{-1}}$
and
![]() $\unicode[STIX]{x1D70C}\text{sp}\prime$
have the same endo-class in
$\unicode[STIX]{x1D70C}\text{sp}\prime$
have the same endo-class in
![]() $\mathscr{E}(\text{K})$
. But the
$\mathscr{E}(\text{K})$
. But the
![]() $\text{K}$
-endo-class of
$\text{K}$
-endo-class of
![]() $\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D6FC}^{-1}}$
(respectively, of
$\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D6FC}^{-1}}$
(respectively, of
![]() $\unicode[STIX]{x1D70C}\text{sp}\prime$
) is a
$\unicode[STIX]{x1D70C}\text{sp}\prime$
) is a
![]() $\text{K}/\text{F}$
-lift of the
$\text{K}/\text{F}$
-lift of the
![]() $\text{F}$
-endo-class of
$\text{F}$
-endo-class of
![]() $\unicode[STIX]{x1D70B}$
(respectively, of
$\unicode[STIX]{x1D70B}$
(respectively, of
![]() $\unicode[STIX]{x1D70B}\text{sp}\prime$
) in the sense of [Reference Bushnell and HenniartBH96, Definition 9.7]. It follows (for instance by applying the restriction map of [Reference Bushnell and HenniartBH96, Corollary 9.13] from
$\unicode[STIX]{x1D70B}\text{sp}\prime$
) in the sense of [Reference Bushnell and HenniartBH96, Definition 9.7]. It follows (for instance by applying the restriction map of [Reference Bushnell and HenniartBH96, Corollary 9.13] from
![]() $\mathscr{E}(\text{K})$
to
$\mathscr{E}(\text{K})$
to
![]() $\mathscr{E}(\text{F})$
) that
$\mathscr{E}(\text{F})$
) that
![]() $\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}$
and
![]() $\unicode[STIX]{x1D70B}\text{sp}\prime$
have the same
$\unicode[STIX]{x1D70B}\text{sp}\prime$
have the same
![]() $\text{F}$
-endo-class. Thus we have proved Theorem A of the introduction, restated here.
$\text{F}$
-endo-class. Thus we have proved Theorem A of the introduction, restated here.
Theorem 7.1. Assume that, for all
![]() $\text{F}$
and
$\text{F}$
and
![]() $n$
and for all maximal totally ramified, cuspidal irreducible complex representations
$n$
and for all maximal totally ramified, cuspidal irreducible complex representations
![]() $\unicode[STIX]{x1D70C}$
of
$\unicode[STIX]{x1D70C}$
of
![]() $\text{G}$
, the representations
$\text{G}$
, the representations
![]() $\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D70C}$
and
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C})$
have the same endo-class. Then the map
$\boldsymbol{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C})$
have the same endo-class. Then the map
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}_{1}$
is the identity.
$\boldsymbol{\unicode[STIX]{x1D70B}}_{1}$
is the identity.
8 Explicit Jacquet–Langlands correspondence up to unramified twist
Now let us fix an endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}\in \mathscr{E}_{n}(\text{F})$
and suppose that
$\boldsymbol{\unicode[STIX]{x1D6E9}}\in \mathscr{E}_{n}(\text{F})$
and suppose that
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}_{1}(\boldsymbol{\unicode[STIX]{x1D6E9}})=\boldsymbol{\unicode[STIX]{x1D6E9}}$
. Write
$\boldsymbol{\unicode[STIX]{x1D70B}}_{1}(\boldsymbol{\unicode[STIX]{x1D6E9}})=\boldsymbol{\unicode[STIX]{x1D6E9}}$
. Write
![]() $\mathscr{D}_{0}(\text{G},\boldsymbol{\unicode[STIX]{x1D6E9}})$
for the set of inertial classes of discrete series representations of
$\mathscr{D}_{0}(\text{G},\boldsymbol{\unicode[STIX]{x1D6E9}})$
for the set of inertial classes of discrete series representations of
![]() $\text{G}$
with endo-class
$\text{G}$
with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
. The local Jacquet–Langlands correspondence (6.1) thus induces a bijective map
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
. The local Jacquet–Langlands correspondence (6.1) thus induces a bijective map
The cuspidal support induces a bijection between
![]() $\mathscr{D}_{0}(\text{G},\boldsymbol{\unicode[STIX]{x1D6E9}})$
and the set of inertial classes of simple supercuspidal pairs of
$\mathscr{D}_{0}(\text{G},\boldsymbol{\unicode[STIX]{x1D6E9}})$
and the set of inertial classes of simple supercuspidal pairs of
![]() $\text{G}$
with endo-class
$\text{G}$
with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
.
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
.
8.1
We fix a simple stratum
![]() $[\mathfrak{a},\unicode[STIX]{x1D6FD}]$
in
$[\mathfrak{a},\unicode[STIX]{x1D6FD}]$
in
![]() $\text{M}_{m}(\text{D})$
such that
$\text{M}_{m}(\text{D})$
such that
![]() $\mathfrak{b}=\mathfrak{a}\,\cap \,\text{B}$
is maximal in
$\mathfrak{b}=\mathfrak{a}\,\cap \,\text{B}$
is maximal in
![]() $\text{B}$
, together with a simple character
$\text{B}$
, together with a simple character
![]() $\unicode[STIX]{x1D703}\in \mathscr{C}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
with endo-class
$\unicode[STIX]{x1D703}\in \mathscr{C}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
and a
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
and a
![]() $\unicode[STIX]{x1D6FD}$
-extension
$\unicode[STIX]{x1D6FD}$
-extension
![]() $\unicode[STIX]{x1D705}$
of
$\unicode[STIX]{x1D705}$
of
![]() $\unicode[STIX]{x1D703}$
. The integer
$\unicode[STIX]{x1D703}$
. The integer
![]() $m\text{sp}\prime$
coming from (3.3) is
$m\text{sp}\prime$
coming from (3.3) is
![]() $m\text{sp}\prime =m(d,g)/g$
, where
$m\text{sp}\prime =m(d,g)/g$
, where
![]() $g$
denotes the degree of
$g$
denotes the degree of
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
. Write
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
. Write
![]() $\text{X}$
for the group of complex characters of
$\text{X}$
for the group of complex characters of
![]() $\boldsymbol{k}^{\times }$
. Thanks to Proposition 3.5 (see also (3.7)), we have a bijective map
$\boldsymbol{k}^{\times }$
. Thanks to Proposition 3.5 (see also (3.7)), we have a bijective map
where
![]() $\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D6FC})$
is the inertial class of discrete series representations of
$\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D6FC})$
is the inertial class of discrete series representations of
![]() $\text{G}$
that contain the simple type
$\text{G}$
that contain the simple type
![]() $\boldsymbol{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})$
.
$\boldsymbol{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})$
.
Similarly, we choose a maximal simple character
![]() $\unicode[STIX]{x1D703}\text{sp}\prime \in \mathscr{C}(\mathfrak{a}\text{sp}\prime ,\unicode[STIX]{x1D6FD}\text{sp}\prime )$
in
$\unicode[STIX]{x1D703}\text{sp}\prime \in \mathscr{C}(\mathfrak{a}\text{sp}\prime ,\unicode[STIX]{x1D6FD}\text{sp}\prime )$
in
![]() $\text{H}$
with endo-class
$\text{H}$
with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
, together with a maximal
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
, together with a maximal
![]() $\unicode[STIX]{x1D6FD}$
-extension
$\unicode[STIX]{x1D6FD}$
-extension
![]() $\unicode[STIX]{x1D705}\text{sp}\prime$
of
$\unicode[STIX]{x1D705}\text{sp}\prime$
of
![]() $\unicode[STIX]{x1D703}\text{sp}\prime$
. We fix a finite extension
$\unicode[STIX]{x1D703}\text{sp}\prime$
. We fix a finite extension
![]() $\boldsymbol{k}\text{sp}\prime$
of the residue field
$\boldsymbol{k}\text{sp}\prime$
of the residue field
![]() $\boldsymbol{e}\text{sp}\prime$
of
$\boldsymbol{e}\text{sp}\prime$
of
![]() $\text{F}[\unicode[STIX]{x1D6FD}\text{sp}\prime ]$
of degree
$\text{F}[\unicode[STIX]{x1D6FD}\text{sp}\prime ]$
of degree
![]() $n\text{sp}\prime =n/g$
, which gives us a parameter set
$n\text{sp}\prime =n/g$
, which gives us a parameter set
![]() $\text{X}\text{sp}\prime /\unicode[STIX]{x1D6E4}\text{sp}\prime$
. We thus get a bijection
$\text{X}\text{sp}\prime /\unicode[STIX]{x1D6E4}\text{sp}\prime$
. We thus get a bijection
![]() $[\unicode[STIX]{x1D6FC}\text{sp}\prime ]\mapsto \unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D705}\text{sp}\prime ,\unicode[STIX]{x1D6FC}\text{sp}\prime )$
between
$[\unicode[STIX]{x1D6FC}\text{sp}\prime ]\mapsto \unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D705}\text{sp}\prime ,\unicode[STIX]{x1D6FC}\text{sp}\prime )$
between
![]() $\text{X}\text{sp}\prime /\unicode[STIX]{x1D6E4}\text{sp}\prime$
and
$\text{X}\text{sp}\prime /\unicode[STIX]{x1D6E4}\text{sp}\prime$
and
![]() $\mathscr{D}_{0}(\text{H},\boldsymbol{\unicode[STIX]{x1D6E9}})$
, similar to (8.2).
$\mathscr{D}_{0}(\text{H},\boldsymbol{\unicode[STIX]{x1D6E9}})$
, similar to (8.2).
Let us fix an isomorphism of
![]() $\boldsymbol{f}$
-extensions
$\boldsymbol{f}$
-extensions
![]() $\boldsymbol{e}\simeq \boldsymbol{e}\text{sp}\prime$
, where
$\boldsymbol{e}\simeq \boldsymbol{e}\text{sp}\prime$
, where
![]() $\boldsymbol{f}$
denotes the residue field of
$\boldsymbol{f}$
denotes the residue field of
![]() $\text{F}$
. We may thus assume that
$\text{F}$
. We may thus assume that
![]() $\boldsymbol{k}\text{sp}\prime =\boldsymbol{k}$
, which identifies the parameter sets
$\boldsymbol{k}\text{sp}\prime =\boldsymbol{k}$
, which identifies the parameter sets
![]() $\text{X}\text{sp}\prime /\unicode[STIX]{x1D6E4}\text{sp}\prime$
and
$\text{X}\text{sp}\prime /\unicode[STIX]{x1D6E4}\text{sp}\prime$
and
![]() $\text{X}/\unicode[STIX]{x1D6E4}$
. Let
$\text{X}/\unicode[STIX]{x1D6E4}$
. Let
![]() $\unicode[STIX]{x1D6F6}$
be the unique bijective map such that the diagram
$\unicode[STIX]{x1D6F6}$
be the unique bijective map such that the diagram

is commutative, where the vertical maps are given by (8.2) and its analogue for
![]() $\text{H}$
. It depends on the choice of the maximal
$\text{H}$
. It depends on the choice of the maximal
![]() $\unicode[STIX]{x1D6FD}$
-extensions
$\unicode[STIX]{x1D6FD}$
-extensions
![]() $\unicode[STIX]{x1D705}$
and
$\unicode[STIX]{x1D705}$
and
![]() $\unicode[STIX]{x1D705}\text{sp}\prime$
, as well as on the
$\unicode[STIX]{x1D705}\text{sp}\prime$
, as well as on the
![]() $\boldsymbol{f}$
-isomorphism
$\boldsymbol{f}$
-isomorphism
![]() $\boldsymbol{e}\simeq \boldsymbol{e}\text{sp}\prime$
(see Remark 3.7 for the dependency in
$\boldsymbol{e}\simeq \boldsymbol{e}\text{sp}\prime$
(see Remark 3.7 for the dependency in
![]() $\boldsymbol{k}$
). We would like to describe
$\boldsymbol{k}$
). We would like to describe
![]() $\unicode[STIX]{x1D6F6}$
. The purpose of Proposition 8.8 below is to show that, in a certain sense, by considering various
$\unicode[STIX]{x1D6F6}$
. The purpose of Proposition 8.8 below is to show that, in a certain sense, by considering various
![]() $m\geqslant 1$
such that
$m\geqslant 1$
such that
![]() $md$
is divisible by the degree of
$md$
is divisible by the degree of
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
, one can reduce the computation of
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
, one can reduce the computation of
![]() $\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FC}])$
to the case where
$\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FC}])$
to the case where
![]() $\unicode[STIX]{x1D6FC}$
is suitably regular.
$\unicode[STIX]{x1D6FC}$
is suitably regular.
By Proposition 5.5 and Corollary 6.2, we have the following fact.
Proposition 8.1. For any prime number
![]() $\ell$
, the bijection
$\ell$
, the bijection
![]() $\unicode[STIX]{x1D6F6}$
is compatible with taking
$\unicode[STIX]{x1D6F6}$
is compatible with taking
![]() $\ell$
-regular parts. More precisely, the
$\ell$
-regular parts. More precisely, the
![]() $\unicode[STIX]{x1D6E4}$
-orbits of
$\unicode[STIX]{x1D6E4}$
-orbits of
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \text{X}$
have the same
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \text{X}$
have the same
![]() $\ell$
-regular part if and only if the
$\ell$
-regular part if and only if the
![]() $\unicode[STIX]{x1D6E4}$
-orbits
$\unicode[STIX]{x1D6E4}$
-orbits
![]() $\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FC}])$
and
$\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FC}])$
and
![]() $\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FD}])$
have the same
$\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FD}])$
have the same
![]() $\ell$
-regular part.
$\ell$
-regular part.
Proposition 8.1 suggests that, with a suitable choice of
![]() $\ell$
, it may be possible to deduce
$\ell$
, it may be possible to deduce
![]() $\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FC}])$
from the knowledge of
$\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FC}])$
from the knowledge of
![]() $\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FD}])$
. We will illustrate this idea in Proposition 8.8 below.
$\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FD}])$
. We will illustrate this idea in Proposition 8.8 below.
8.2
We first give another property of the map
![]() $\unicode[STIX]{x1D6F6}$
. Set
$\unicode[STIX]{x1D6F6}$
. Set
![]() $n\text{sp}\prime =n/g=m\text{sp}\prime d\text{sp}\prime$
. Given
$n\text{sp}\prime =n/g=m\text{sp}\prime d\text{sp}\prime$
. Given
![]() $\unicode[STIX]{x1D6FC}\in \text{X}$
, let
$\unicode[STIX]{x1D6FC}\in \text{X}$
, let
![]() $f$
be the cardinality of its
$f$
be the cardinality of its
![]() $\unicode[STIX]{x1D6E4}$
-orbit, and write
$\unicode[STIX]{x1D6E4}$
-orbit, and write
Recall that
![]() $d\text{sp}\prime$
is the degree of
$d\text{sp}\prime$
is the degree of
![]() $\boldsymbol{d}$
over
$\boldsymbol{d}$
over
![]() $\boldsymbol{e}$
(the residue field of
$\boldsymbol{e}$
(the residue field of
![]() $\text{F}[\unicode[STIX]{x1D6FD}]$
), so
$\text{F}[\unicode[STIX]{x1D6FD}]$
), so
![]() $d\text{sp}\prime =d/(d,g)$
. Note that the cardinality of its
$d\text{sp}\prime =d/(d,g)$
. Note that the cardinality of its
![]() $\text{Gal}(\boldsymbol{k}/\boldsymbol{d})$
-orbit is equal to
$\text{Gal}(\boldsymbol{k}/\boldsymbol{d})$
-orbit is equal to
![]() $f/(f,d\text{sp}\prime )$
, which was denoted by
$f/(f,d\text{sp}\prime )$
, which was denoted by
![]() $u$
in § 3.3.
$u$
in § 3.3.
Definition 8.2. We call the integer
![]() $f$
the parametric degree of
$f$
the parametric degree of
![]() $\unicode[STIX]{x1D6FC}\in \text{X}$
.
$\unicode[STIX]{x1D6FC}\in \text{X}$
.
This is related to the notion of parametric degree for a discrete series representation as follows: any discrete series representation in
![]() $\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D6FC})$
has parametric degree
$\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D6FC})$
has parametric degree
![]() $fg$
.
$fg$
.
Since the local Jacquet–Langlands correspondence preserves the parametric degree (see [Reference Bushnell and HenniartBH11a]), we have the following result.
Lemma 8.3. For all
![]() $\unicode[STIX]{x1D6FC}\in \text{X}$
, the parametric degrees of
$\unicode[STIX]{x1D6FC}\in \text{X}$
, the parametric degrees of
![]() $[\unicode[STIX]{x1D6FC}]$
and
$[\unicode[STIX]{x1D6FC}]$
and
![]() $\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FC}])$
are equal.
$\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FC}])$
are equal.
Note that
![]() $\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D6FC})$
is made of cuspidal representations with cuspidal Jacquet–Langlands transfers if and only if
$\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D6FC})$
is made of cuspidal representations with cuspidal Jacquet–Langlands transfers if and only if
![]() $f=n\text{sp}\prime$
, that is, if and only if
$f=n\text{sp}\prime$
, that is, if and only if
![]() $\unicode[STIX]{x1D6FC}$
is
$\unicode[STIX]{x1D6FC}$
is
![]() $\boldsymbol{e}$
-regular. Indeed, from [Reference Bushnell and HenniartBH11a], a discrete series representation of
$\boldsymbol{e}$
-regular. Indeed, from [Reference Bushnell and HenniartBH11a], a discrete series representation of
![]() $\text{G}$
is cuspidal with cuspidal Jacquet–Langlands transfer if and only if its parametric degree is
$\text{G}$
is cuspidal with cuspidal Jacquet–Langlands transfer if and only if its parametric degree is
![]() $n$
.
$n$
.
8.3
Let
![]() $a\geqslant 1$
be a positive integer. We consider the simple stratum
$a\geqslant 1$
be a positive integer. We consider the simple stratum
![]() $[\mathfrak{a}^{\ast },\unicode[STIX]{x1D6FD}]$
in
$[\mathfrak{a}^{\ast },\unicode[STIX]{x1D6FD}]$
in
![]() $\text{M}_{am}(\text{D})$
, where
$\text{M}_{am}(\text{D})$
, where
![]() $\mathfrak{a}^{\ast }$
is the hereditary order
$\mathfrak{a}^{\ast }$
is the hereditary order
![]() $\text{M}_{a}(\mathfrak{a})$
, and write
$\text{M}_{a}(\mathfrak{a})$
, and write
![]() $\unicode[STIX]{x1D703}^{\ast }\in \mathscr{C}(\mathfrak{a}^{\ast },\unicode[STIX]{x1D6FD})$
for the transfer of
$\unicode[STIX]{x1D703}^{\ast }\in \mathscr{C}(\mathfrak{a}^{\ast },\unicode[STIX]{x1D6FD})$
for the transfer of
![]() $\unicode[STIX]{x1D703}$
in the sense of [Reference SécherreSéc04, 3.3.3]. Associated with
$\unicode[STIX]{x1D703}$
in the sense of [Reference SécherreSéc04, 3.3.3]. Associated with
![]() $\unicode[STIX]{x1D705}$
is a coherent choice of a maximal
$\unicode[STIX]{x1D705}$
is a coherent choice of a maximal
![]() $\unicode[STIX]{x1D6FD}$
-extension
$\unicode[STIX]{x1D6FD}$
-extension
![]() $\unicode[STIX]{x1D705}^{\ast }$
of the simple character
$\unicode[STIX]{x1D705}^{\ast }$
of the simple character
![]() $\unicode[STIX]{x1D703}^{\ast }$
(see [Reference Mínguez and SécherreMS14b, Remarque 5.17]). We fix a finite extension
$\unicode[STIX]{x1D703}^{\ast }$
(see [Reference Mínguez and SécherreMS14b, Remarque 5.17]). We fix a finite extension
![]() $\boldsymbol{k}^{\ast }$
of
$\boldsymbol{k}^{\ast }$
of
![]() $\boldsymbol{k}$
of degree
$\boldsymbol{k}$
of degree
![]() $a$
. Write
$a$
. Write
![]() $\text{X}^{\ast }$
for the group of complex characters of
$\text{X}^{\ast }$
for the group of complex characters of
![]() $\boldsymbol{k}^{\ast \times }$
and
$\boldsymbol{k}^{\ast \times }$
and
![]() $\unicode[STIX]{x1D6E4}^{\ast }$
for the Galois group of
$\unicode[STIX]{x1D6E4}^{\ast }$
for the Galois group of
![]() $\boldsymbol{k}^{\ast }/\boldsymbol{e}$
. Repeating the arguments of § 8.1 with
$\boldsymbol{k}^{\ast }/\boldsymbol{e}$
. Repeating the arguments of § 8.1 with
![]() $\text{GL}_{am}(\text{D})$
and
$\text{GL}_{am}(\text{D})$
and
![]() $\text{GL}_{an}(\text{F})$
, we get a bijective map
$\text{GL}_{an}(\text{F})$
, we get a bijective map
![]() $\unicode[STIX]{x1D6F6}^{\ast }:\text{X}^{\ast }/\unicode[STIX]{x1D6E4}^{\ast }\rightarrow \text{X}^{\ast }/\unicode[STIX]{x1D6E4}^{\ast }$
. We have the following straightforward result.
$\unicode[STIX]{x1D6F6}^{\ast }:\text{X}^{\ast }/\unicode[STIX]{x1D6E4}^{\ast }\rightarrow \text{X}^{\ast }/\unicode[STIX]{x1D6E4}^{\ast }$
. We have the following straightforward result.
Lemma 8.4. Let
![]() $[\unicode[STIX]{x1D6FC}]\in \text{X}/\unicode[STIX]{x1D6E4}$
, and let
$[\unicode[STIX]{x1D6FC}]\in \text{X}/\unicode[STIX]{x1D6E4}$
, and let
![]() $\text{L}(\unicode[STIX]{x1D70C},r)$
be in the inertial class
$\text{L}(\unicode[STIX]{x1D70C},r)$
be in the inertial class
![]() $\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D6FC})$
for some integer
$\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D6FC})$
for some integer
![]() $r$
dividing
$r$
dividing
![]() $m$
and some irreducible cuspidal representation
$m$
and some irreducible cuspidal representation
![]() $\unicode[STIX]{x1D70C}$
of
$\unicode[STIX]{x1D70C}$
of
![]() $\text{GL}_{m/r}(\text{D})$
. Then
$\text{GL}_{m/r}(\text{D})$
. Then
![]() $\text{L}(\unicode[STIX]{x1D70C},ar)$
is in the inertial class
$\text{L}(\unicode[STIX]{x1D70C},ar)$
is in the inertial class
![]() $\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D705}^{\ast },\unicode[STIX]{x1D6FC}^{\ast })$
, where
$\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D705}^{\ast },\unicode[STIX]{x1D6FC}^{\ast })$
, where
![]() $\unicode[STIX]{x1D6FC}^{\ast }$
is the character
$\unicode[STIX]{x1D6FC}^{\ast }$
is the character
![]() $\unicode[STIX]{x1D6FC}\circ \text{N}_{\boldsymbol{k}^{\ast }/\boldsymbol{k}}$
of
$\unicode[STIX]{x1D6FC}\circ \text{N}_{\boldsymbol{k}^{\ast }/\boldsymbol{k}}$
of
![]() $\boldsymbol{k}^{\ast \times }$
.
$\boldsymbol{k}^{\ast \times }$
.
Proof. With the notation of § 3.3 and writing
![]() $\text{M}$
for the Levi subgroup
$\text{M}$
for the Levi subgroup
![]() $\text{G}\times \cdots \times \text{G}\subseteq \text{GL}_{am}(\text{D})$
and
$\text{G}\times \cdots \times \text{G}\subseteq \text{GL}_{am}(\text{D})$
and
![]() $\text{U}$
for the unipotent radical of the parabolic subgroup composed of upper
$\text{U}$
for the unipotent radical of the parabolic subgroup composed of upper
![]() $a\times a$
block-triangular matrices of
$a\times a$
block-triangular matrices of
![]() $\text{GL}_{am}(\text{D})$
, this follows from the fact that the representation of
$\text{GL}_{am}(\text{D})$
, this follows from the fact that the representation of
![]() $\text{J}(\mathfrak{a}_{r}^{\ast },\unicode[STIX]{x1D6FD})\,\cap \,\text{M}$
on the
$\text{J}(\mathfrak{a}_{r}^{\ast },\unicode[STIX]{x1D6FD})\,\cap \,\text{M}$
on the
![]() $\text{J}(\mathfrak{a}_{r}^{\ast },\unicode[STIX]{x1D6FD})\,\cap \,\text{U}$
-invariant subspace of the transfer
$\text{J}(\mathfrak{a}_{r}^{\ast },\unicode[STIX]{x1D6FD})\,\cap \,\text{U}$
-invariant subspace of the transfer
![]() $\unicode[STIX]{x1D705}_{ar}^{\ast }$
of
$\unicode[STIX]{x1D705}_{ar}^{\ast }$
of
![]() $\unicode[STIX]{x1D705}^{\ast }$
to
$\unicode[STIX]{x1D705}^{\ast }$
to
![]() $\text{J}(\mathfrak{a}_{ar}^{\ast },\unicode[STIX]{x1D6FD})$
is
$\text{J}(\mathfrak{a}_{ar}^{\ast },\unicode[STIX]{x1D6FD})$
is
![]() $\unicode[STIX]{x1D705}\otimes \cdots \otimes \unicode[STIX]{x1D705}$
.◻
$\unicode[STIX]{x1D705}\otimes \cdots \otimes \unicode[STIX]{x1D705}$
.◻
For
![]() $\unicode[STIX]{x1D6FC}\in \text{X}$
, the orbit
$\unicode[STIX]{x1D6FC}\in \text{X}$
, the orbit
![]() $[\unicode[STIX]{x1D6FC}^{\ast }]$
depends only on
$[\unicode[STIX]{x1D6FC}^{\ast }]$
depends only on
![]() $[\unicode[STIX]{x1D6FC}]$
, and we denote it
$[\unicode[STIX]{x1D6FC}]$
, and we denote it
![]() $[\unicode[STIX]{x1D6FC}]^{\ast }$
. By Lemma 8.4 we therefore have
$[\unicode[STIX]{x1D6FC}]^{\ast }$
. By Lemma 8.4 we therefore have
for any character
![]() $\unicode[STIX]{x1D6FC}\in \text{X}$
.
$\unicode[STIX]{x1D6FC}\in \text{X}$
.
Given
![]() $\unicode[STIX]{x1D6FC}\in \text{X}$
, we write
$\unicode[STIX]{x1D6FC}\in \text{X}$
, we write
![]() $f$
for its parametric degree and
$f$
for its parametric degree and
![]() $\boldsymbol{e}[\unicode[STIX]{x1D6FC}]$
for the subfield of
$\boldsymbol{e}[\unicode[STIX]{x1D6FC}]$
for the subfield of
![]() $\boldsymbol{k}$
of degree
$\boldsymbol{k}$
of degree
![]() $f$
over
$f$
over
![]() $\boldsymbol{e}$
.
$\boldsymbol{e}$
.
Lemma 8.5. Let
![]() $\unicode[STIX]{x1D6FC}\in \text{X}$
. There exist an integer
$\unicode[STIX]{x1D6FC}\in \text{X}$
. There exist an integer
![]() $a\geqslant 1$
, a prime number
$a\geqslant 1$
, a prime number
![]() $\ell \neq p$
not dividing the order of
$\ell \neq p$
not dividing the order of
![]() $\boldsymbol{e}[\unicode[STIX]{x1D6FC}]^{\times }$
and an
$\boldsymbol{e}[\unicode[STIX]{x1D6FC}]^{\times }$
and an
![]() $\boldsymbol{e}$
-regular character
$\boldsymbol{e}$
-regular character
![]() $\unicode[STIX]{x1D6FD}\in \text{X}^{\ast }$
such that
$\unicode[STIX]{x1D6FD}\in \text{X}^{\ast }$
such that
![]() $\unicode[STIX]{x1D6FD}\equiv \unicode[STIX]{x1D6FC}^{\ast }$
mod
$\unicode[STIX]{x1D6FD}\equiv \unicode[STIX]{x1D6FC}^{\ast }$
mod
![]() $\ell$
.
$\ell$
.
Proof. First recall the following result, known as Zsigmondy’s Theorem [Reference ZsigmondyZsi92].
Lemma 8.6. Let
![]() $b,r\geqslant 2$
be integers. There exists a prime number
$b,r\geqslant 2$
be integers. There exists a prime number
![]() $\ell$
which divides
$\ell$
which divides
![]() $b^{r}-1$
but not
$b^{r}-1$
but not
![]() $b^{i}-1$
for any
$b^{i}-1$
for any
![]() $i\in \{1,\ldots ,r-1\}$
, except when
$i\in \{1,\ldots ,r-1\}$
, except when
![]() $r=6$
and
$r=6$
and
![]() $b=2$
, and when
$b=2$
, and when
![]() $r=2$
and
$r=2$
and
![]() $b=2^{k}-1$
for some
$b=2^{k}-1$
for some
![]() $k\geqslant 1$
.
$k\geqslant 1$
.
Let us write
![]() $\text{Q}$
for the cardinality of
$\text{Q}$
for the cardinality of
![]() $\boldsymbol{e}$
, and let us fix an
$\boldsymbol{e}$
, and let us fix an
![]() $a\geqslant 1$
such that
$a\geqslant 1$
such that
![]() $an\text{sp}\prime >6f$
. Applying Lemma 8.6 with
$an\text{sp}\prime >6f$
. Applying Lemma 8.6 with
![]() $b=\text{Q}^{f}$
and
$b=\text{Q}^{f}$
and
![]() $r=an\text{sp}\prime /f$
, we obtain a prime number
$r=an\text{sp}\prime /f$
, we obtain a prime number
![]() $\ell$
dividing
$\ell$
dividing
![]() $b^{r}-1$
but not dividing
$b^{r}-1$
but not dividing
![]() $b^{i}-1$
for any
$b^{i}-1$
for any
![]() $i\in \{1,\ldots ,r-1\}$
. It follows that
$i\in \{1,\ldots ,r-1\}$
. It follows that
![]() $b$
has order
$b$
has order
![]() $r$
in the group
$r$
in the group
![]() $(\mathbf{Z}/\ell \mathbf{Z})^{\times }$
.
$(\mathbf{Z}/\ell \mathbf{Z})^{\times }$
.
Let
![]() $\unicode[STIX]{x1D709}$
be a non-trivial character of
$\unicode[STIX]{x1D709}$
be a non-trivial character of
![]() $\boldsymbol{k}^{\ast \times }$
of order
$\boldsymbol{k}^{\ast \times }$
of order
![]() $\ell$
. Then the character
$\ell$
. Then the character
![]() $\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D709}\unicode[STIX]{x1D6FC}^{\ast }$
is congruent to
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D709}\unicode[STIX]{x1D6FC}^{\ast }$
is congruent to
![]() $\unicode[STIX]{x1D6FC}^{\ast }$
mod
$\unicode[STIX]{x1D6FC}^{\ast }$
mod
![]() $\ell$
. Since the order of
$\ell$
. Since the order of
![]() $\unicode[STIX]{x1D6FC}$
is prime to
$\unicode[STIX]{x1D6FC}$
is prime to
![]() $\ell$
(for it divides
$\ell$
(for it divides
![]() $b-1$
), the cardinality of the
$b-1$
), the cardinality of the
![]() $\unicode[STIX]{x1D6E4}$
-orbit of
$\unicode[STIX]{x1D6E4}$
-orbit of
![]() $\unicode[STIX]{x1D6FD}$
is the least common multiple of
$\unicode[STIX]{x1D6FD}$
is the least common multiple of
![]() $f$
and the order of
$f$
and the order of
![]() $\text{Q}$
in
$\text{Q}$
in
![]() $(\mathbf{Z}/\ell \mathbf{Z})^{\times }$
. This cardinality is equal to
$(\mathbf{Z}/\ell \mathbf{Z})^{\times }$
. This cardinality is equal to
![]() $fr=an\text{sp}\prime$
, and hence
$fr=an\text{sp}\prime$
, and hence
![]() $\unicode[STIX]{x1D6FD}$
is
$\unicode[STIX]{x1D6FD}$
is
![]() $\boldsymbol{e}$
-regular.◻
$\boldsymbol{e}$
-regular.◻
Remark 8.7. (1) The choice
![]() $a=1$
is not always possible. For instance, if
$a=1$
is not always possible. For instance, if
![]() $\unicode[STIX]{x1D6FC}$
is trivial,
$\unicode[STIX]{x1D6FC}$
is trivial,
![]() $\boldsymbol{e}$
has seven elements and
$\boldsymbol{e}$
has seven elements and
![]() $n\text{sp}\prime =2$
, then no prime number
$n\text{sp}\prime =2$
, then no prime number
![]() $\ell$
satisfies the required condition. We thank Guy Henniart for a suggestion that led us to introduce the process described here.
$\ell$
satisfies the required condition. We thank Guy Henniart for a suggestion that led us to introduce the process described here.
(2) The proof of Lemma 8.5 shows that for any character
![]() $\unicode[STIX]{x1D6FC}\in \text{X}$
, we can choose
$\unicode[STIX]{x1D6FC}\in \text{X}$
, we can choose
![]() $a$
to be any integer greater than or equal to
$a$
to be any integer greater than or equal to
![]() $7$
. Moreover, the choices of
$7$
. Moreover, the choices of
![]() $a$
and
$a$
and
![]() $\ell$
depend only on the parametric degree
$\ell$
depend only on the parametric degree
![]() $f$
, not on
$f$
, not on
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.
(3) Note that
![]() $\ell$
cannot be
$\ell$
cannot be
![]() $2$
. Indeed, we have
$2$
. Indeed, we have
![]() $\ell \neq p$
, and if
$\ell \neq p$
, and if
![]() $p$
is odd, then the fact that
$p$
is odd, then the fact that
![]() $\ell$
does not divide
$\ell$
does not divide
![]() $\text{Q}^{f}-1$
(the order of
$\text{Q}^{f}-1$
(the order of
![]() $\boldsymbol{e}[\unicode[STIX]{x1D6FC}]^{\times }$
) implies that
$\boldsymbol{e}[\unicode[STIX]{x1D6FC}]^{\times }$
) implies that
![]() $\ell \neq 2$
.
$\ell \neq 2$
.
With the notation of Lemma 8.5, we get the following result.
Proposition 8.8. Assume that
![]() $\unicode[STIX]{x1D6F6}^{\ast }([\unicode[STIX]{x1D6FD}])=[\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D707}]$
for some character
$\unicode[STIX]{x1D6F6}^{\ast }([\unicode[STIX]{x1D6FD}])=[\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D707}]$
for some character
![]() $\unicode[STIX]{x1D707}\in \text{X}^{\ast }$
. Then
$\unicode[STIX]{x1D707}\in \text{X}^{\ast }$
. Then
![]() $\unicode[STIX]{x1D707}_{\ell }=\unicode[STIX]{x1D708}^{\ast }$
for some character
$\unicode[STIX]{x1D707}_{\ell }=\unicode[STIX]{x1D708}^{\ast }$
for some character
![]() $\unicode[STIX]{x1D708}\in \text{X}$
and we have
$\unicode[STIX]{x1D708}\in \text{X}$
and we have
![]() $\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FC}])=[\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D708}]$
.
$\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FC}])=[\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D708}]$
.
Proof. Let us write
![]() $\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FC}])=[\unicode[STIX]{x1D6FC}\text{sp}\prime ]$
for some
$\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FC}])=[\unicode[STIX]{x1D6FC}\text{sp}\prime ]$
for some
![]() $\unicode[STIX]{x1D6FC}\text{sp}\prime \in \text{X}$
. Then
$\unicode[STIX]{x1D6FC}\text{sp}\prime \in \text{X}$
. Then
![]() $[\unicode[STIX]{x1D6FC}\text{sp}\prime ^{\ast }]\equiv [\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D707}]$
mod
$[\unicode[STIX]{x1D6FC}\text{sp}\prime ^{\ast }]\equiv [\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D707}]$
mod
![]() $\ell$
. By Lemma 8.3, the parametric degree of
$\ell$
. By Lemma 8.3, the parametric degree of
![]() $\unicode[STIX]{x1D6FC}\text{sp}\prime$
is
$\unicode[STIX]{x1D6FC}\text{sp}\prime$
is
![]() $f$
, and so
$f$
, and so
![]() $\boldsymbol{e}[\unicode[STIX]{x1D6FC}\text{sp}\prime ]=\boldsymbol{e}[\unicode[STIX]{x1D6FC}]$
. It follows that
$\boldsymbol{e}[\unicode[STIX]{x1D6FC}\text{sp}\prime ]=\boldsymbol{e}[\unicode[STIX]{x1D6FC}]$
. It follows that
![]() $\ell$
does not divide the order of
$\ell$
does not divide the order of
![]() $\unicode[STIX]{x1D6FC}\text{sp}\prime$
. Write
$\unicode[STIX]{x1D6FC}\text{sp}\prime$
. Write
![]() $\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D709}\unicode[STIX]{x1D6FC}^{\ast }$
for some character
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D709}\unicode[STIX]{x1D6FC}^{\ast }$
for some character
![]() $\unicode[STIX]{x1D709}$
whose order is a power of
$\unicode[STIX]{x1D709}$
whose order is a power of
![]() $\ell$
. Taking
$\ell$
. Taking
![]() $\ell$
-regular parts, we get
$\ell$
-regular parts, we get
![]() $[\unicode[STIX]{x1D6FC}\text{sp}\prime ^{\ast }]_{\ell }^{}=[\unicode[STIX]{x1D6FC}\text{sp}\prime ^{\ast }]=[\unicode[STIX]{x1D6FC}^{\ast }\unicode[STIX]{x1D707}_{\ell }^{}]$
. Changing
$[\unicode[STIX]{x1D6FC}\text{sp}\prime ^{\ast }]_{\ell }^{}=[\unicode[STIX]{x1D6FC}\text{sp}\prime ^{\ast }]=[\unicode[STIX]{x1D6FC}^{\ast }\unicode[STIX]{x1D707}_{\ell }^{}]$
. Changing
![]() $\unicode[STIX]{x1D6FC}\text{sp}\prime$
in its
$\unicode[STIX]{x1D6FC}\text{sp}\prime$
in its
![]() $\unicode[STIX]{x1D6E4}$
-orbit, we may assume that
$\unicode[STIX]{x1D6E4}$
-orbit, we may assume that
![]() $\unicode[STIX]{x1D6FC}\text{sp}\prime ^{\ast }=\unicode[STIX]{x1D6FC}^{\ast }\unicode[STIX]{x1D707}_{\ell }^{}$
. Thus
$\unicode[STIX]{x1D6FC}\text{sp}\prime ^{\ast }=\unicode[STIX]{x1D6FC}^{\ast }\unicode[STIX]{x1D707}_{\ell }^{}$
. Thus
![]() $\unicode[STIX]{x1D707}_{\ell }=\unicode[STIX]{x1D708}^{\ast }$
for some
$\unicode[STIX]{x1D707}_{\ell }=\unicode[STIX]{x1D708}^{\ast }$
for some
![]() $\unicode[STIX]{x1D708}\in \text{X}$
. Since
$\unicode[STIX]{x1D708}\in \text{X}$
. Since
![]() $\text{N}_{\boldsymbol{k}^{\ast }/\boldsymbol{k}}$
is surjective, we get
$\text{N}_{\boldsymbol{k}^{\ast }/\boldsymbol{k}}$
is surjective, we get
![]() $\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FC}])=[\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D708}]$
.◻
$\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FC}])=[\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D708}]$
.◻
9 The essentially tame case
The purpose of this section is to illustrate Proposition 8.8 in the essentially tame case. Assume that
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
is essentially tame; we then have
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
is essentially tame; we then have
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}_{1}(\boldsymbol{\unicode[STIX]{x1D6E9}})=\boldsymbol{\unicode[STIX]{x1D6E9}}$
by Corollary 6.6. As in § 8.1, we will fix maximal simple characters
$\boldsymbol{\unicode[STIX]{x1D70B}}_{1}(\boldsymbol{\unicode[STIX]{x1D6E9}})=\boldsymbol{\unicode[STIX]{x1D6E9}}$
by Corollary 6.6. As in § 8.1, we will fix maximal simple characters
![]() $\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x1D703}$
and
![]() $\unicode[STIX]{x1D703}\text{sp}\prime$
in
$\unicode[STIX]{x1D703}\text{sp}\prime$
in
![]() $\text{G}$
and
$\text{G}$
and
![]() $\text{H}$
with endo-class
$\text{H}$
with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
, but we must be careful here: for our purpose, these choices have to be compatible, in a sense that we will define in § 9.1.
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
, but we must be careful here: for our purpose, these choices have to be compatible, in a sense that we will define in § 9.1.
That we need to take care of this compatibility was brought to our attention by the work of Dotto [Reference DottoDot17], who resolved this rigidity problem in essentially the same way, though with a slightly different language.
Recall (Corollary 6.6 and Lemma 3.3) that the tameness assumption on
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
means that
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
means that
![]() $\text{F}[\unicode[STIX]{x1D6FD}]$
is tamely ramified over
$\text{F}[\unicode[STIX]{x1D6FD}]$
is tamely ramified over
![]() $\text{F}$
, for any simple stratum
$\text{F}$
, for any simple stratum
![]() $[\mathfrak{a},\unicode[STIX]{x1D6FD}]$
and any simple character
$[\mathfrak{a},\unicode[STIX]{x1D6FD}]$
and any simple character
![]() $\unicode[STIX]{x1D703}\in \mathscr{C}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
of endo-class
$\unicode[STIX]{x1D703}\in \mathscr{C}(\mathfrak{a},\unicode[STIX]{x1D6FD})$
of endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
. We will see other properties of essentially tame endo-classes below. We also refer the reader to [Reference Bushnell and HenniartBH05b, § 1] for more details.
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
. We will see other properties of essentially tame endo-classes below. We also refer the reader to [Reference Bushnell and HenniartBH05b, § 1] for more details.
As in § 8, we write
![]() $g$
for the degree of
$g$
for the degree of
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
and set
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
and set
![]() $n\text{sp}\prime =n/g$
.
$n\text{sp}\prime =n/g$
.
9.1
In order to formulate our Compatibility Assumption below, it is convenient to use the notion of ps-character defined in [Reference Broussous, Sécherre and StevensBSS12, Definition 1.5]. Fix once and for all a separable closure
![]() $\overline{\text{F}}$
of
$\overline{\text{F}}$
of
![]() $\text{F}$
. Its residue field
$\text{F}$
. Its residue field
![]() $\overline{\boldsymbol{f}}$
is an algebraic closure of the residue field
$\overline{\boldsymbol{f}}$
is an algebraic closure of the residue field
![]() $\boldsymbol{f}$
of
$\boldsymbol{f}$
of
![]() $\text{F}$
. Let
$\text{F}$
. Let
![]() $\boldsymbol{k}$
be the unique extension of
$\boldsymbol{k}$
be the unique extension of
![]() $\boldsymbol{f}$
of degree
$\boldsymbol{f}$
of degree
![]() $n\text{sp}\prime$
contained in
$n\text{sp}\prime$
contained in
![]() $\overline{\boldsymbol{f}}$
and write
$\overline{\boldsymbol{f}}$
and write
![]() $\text{X}$
for the group of complex characters of
$\text{X}$
for the group of complex characters of
![]() $\boldsymbol{k}^{\times }$
.
$\boldsymbol{k}^{\times }$
.
Let us fix a ps-character
![]() $(\unicode[STIX]{x1D6E9},0,\unicode[STIX]{x1D6FD})$
of endo-class
$(\unicode[STIX]{x1D6E9},0,\unicode[STIX]{x1D6FD})$
of endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
with
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
with
![]() $\unicode[STIX]{x1D6FD}\in \overline{\text{F}}$
. Write
$\unicode[STIX]{x1D6FD}\in \overline{\text{F}}$
. Write
![]() $\text{E}$
for the field
$\text{E}$
for the field
![]() $\text{F}[\unicode[STIX]{x1D6FD}]$
and
$\text{F}[\unicode[STIX]{x1D6FD}]$
and
![]() $\boldsymbol{e}$
for its residue field, which canonically identifies with an extension of
$\boldsymbol{e}$
for its residue field, which canonically identifies with an extension of
![]() $\boldsymbol{f}$
contained in
$\boldsymbol{f}$
contained in
![]() $\boldsymbol{k}$
. Write
$\boldsymbol{k}$
. Write
![]() $\unicode[STIX]{x1D6E4}$
for the Galois group of
$\unicode[STIX]{x1D6E4}$
for the Galois group of
![]() $\boldsymbol{k}$
over
$\boldsymbol{k}$
over
![]() $\boldsymbol{e}$
. Since
$\boldsymbol{e}$
. Since
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
is essentially tame,
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
is essentially tame,
![]() $\text{E}$
is tamely ramified over
$\text{E}$
is tamely ramified over
![]() $\text{F}$
.
$\text{F}$
.
We now fix a homomorphism
![]() $\unicode[STIX]{x1D704}:\text{E}\rightarrow \text{M}_{m}(\text{D})$
of
$\unicode[STIX]{x1D704}:\text{E}\rightarrow \text{M}_{m}(\text{D})$
of
![]() $\text{F}$
-algebras and a principal order
$\text{F}$
-algebras and a principal order
![]() $\mathfrak{a}$
in
$\mathfrak{a}$
in
![]() $\text{M}_{m}(\text{D})$
normalized by
$\text{M}_{m}(\text{D})$
normalized by
![]() $\unicode[STIX]{x1D704}\text{E}^{\times }$
, such that the intersection
$\unicode[STIX]{x1D704}\text{E}^{\times }$
, such that the intersection
![]() $\mathfrak{b}$
of
$\mathfrak{b}$
of
![]() $\mathfrak{a}$
with the centralizer
$\mathfrak{a}$
with the centralizer
![]() $\text{B}$
of
$\text{B}$
of
![]() $\unicode[STIX]{x1D704}\text{E}$
in
$\unicode[STIX]{x1D704}\text{E}$
in
![]() $\text{M}_{m}(\text{D})$
is a maximal order. By [Reference Broussous, Sécherre and StevensBSS12, Definition 1.5], this gives us a maximal simple stratum
$\text{M}_{m}(\text{D})$
is a maximal order. By [Reference Broussous, Sécherre and StevensBSS12, Definition 1.5], this gives us a maximal simple stratum
![]() $[\mathfrak{a},\unicode[STIX]{x1D704}\unicode[STIX]{x1D6FD}]$
in
$[\mathfrak{a},\unicode[STIX]{x1D704}\unicode[STIX]{x1D6FD}]$
in
![]() $\text{M}_{m}(\text{D})$
and a maximal simple character
$\text{M}_{m}(\text{D})$
and a maximal simple character
![]() $\unicode[STIX]{x1D703}\in \mathscr{C}(\mathfrak{a},\unicode[STIX]{x1D704}\unicode[STIX]{x1D6FD})$
of endo-class
$\unicode[STIX]{x1D703}\in \mathscr{C}(\mathfrak{a},\unicode[STIX]{x1D704}\unicode[STIX]{x1D6FD})$
of endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
. This also defines an
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
. This also defines an
![]() $\boldsymbol{f}$
-isomorphism
$\boldsymbol{f}$
-isomorphism
where
![]() $\boldsymbol{e}_{\unicode[STIX]{x1D704}}$
denotes the residue field of
$\boldsymbol{e}_{\unicode[STIX]{x1D704}}$
denotes the residue field of
![]() $\unicode[STIX]{x1D704}\text{E}$
. As in § 3.3, we fix an extension
$\unicode[STIX]{x1D704}\text{E}$
. As in § 3.3, we fix an extension
![]() $\boldsymbol{k}_{\unicode[STIX]{x1D704}}$
of
$\boldsymbol{k}_{\unicode[STIX]{x1D704}}$
of
![]() $\boldsymbol{e}_{\unicode[STIX]{x1D704}}$
. Write
$\boldsymbol{e}_{\unicode[STIX]{x1D704}}$
. Write
![]() $\text{X}_{\unicode[STIX]{x1D704}}$
for the group of complex characters of
$\text{X}_{\unicode[STIX]{x1D704}}$
for the group of complex characters of
![]() $(\boldsymbol{k}_{\unicode[STIX]{x1D704}})^{\times }$
and
$(\boldsymbol{k}_{\unicode[STIX]{x1D704}})^{\times }$
and
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D704}}$
for the Galois group of
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D704}}$
for the Galois group of
![]() $\boldsymbol{k}_{\unicode[STIX]{x1D704}}$
over
$\boldsymbol{k}_{\unicode[STIX]{x1D704}}$
over
![]() $\boldsymbol{e}_{\unicode[STIX]{x1D704}}$
. The
$\boldsymbol{e}_{\unicode[STIX]{x1D704}}$
. The
![]() $\boldsymbol{f}$
-isomorphism
$\boldsymbol{f}$
-isomorphism
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D704}}$
allows us to identify
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D704}}$
allows us to identify
![]() $\text{X}/\unicode[STIX]{x1D6E4}$
and
$\text{X}/\unicode[STIX]{x1D6E4}$
and
![]() $\text{X}_{\unicode[STIX]{x1D704}}/\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D704}}$
. Write
$\text{X}_{\unicode[STIX]{x1D704}}/\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D704}}$
. Write
![]() $\unicode[STIX]{x1D705}$
for the unique
$\unicode[STIX]{x1D705}$
for the unique
![]() $\unicode[STIX]{x1D6FD}$
-extension of
$\unicode[STIX]{x1D6FD}$
-extension of
![]() $\unicode[STIX]{x1D703}$
whose determinant has order a power of
$\unicode[STIX]{x1D703}$
whose determinant has order a power of
![]() $p$
. This choice gives us a bijective map between
$p$
. This choice gives us a bijective map between
![]() $\text{X}_{\unicode[STIX]{x1D704}}/\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D704}}$
and
$\text{X}_{\unicode[STIX]{x1D704}}/\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D704}}$
and
![]() $\mathscr{D}_{0}(\text{G},\boldsymbol{\unicode[STIX]{x1D6E9}})$
as in (8.2). Composing with the identification above, we get a bijection
$\mathscr{D}_{0}(\text{G},\boldsymbol{\unicode[STIX]{x1D6E9}})$
as in (8.2). Composing with the identification above, we get a bijection
denoted by
![]() $\boldsymbol{\unicode[STIX]{x1D714}}$
, which depends on the various choices we have made.
$\boldsymbol{\unicode[STIX]{x1D714}}$
, which depends on the various choices we have made.
Using the same ps-character
![]() $(\unicode[STIX]{x1D6E9},0,\unicode[STIX]{x1D6FD})$
as above, we now make similar choices for
$(\unicode[STIX]{x1D6E9},0,\unicode[STIX]{x1D6FD})$
as above, we now make similar choices for
![]() $\text{H}$
: an
$\text{H}$
: an
![]() $\text{F}$
-homomorphism
$\text{F}$
-homomorphism
![]() $\unicode[STIX]{x1D704}\text{sp}\prime :\text{E}\rightarrow \text{M}_{n}(\text{F})$
and a principal order
$\unicode[STIX]{x1D704}\text{sp}\prime :\text{E}\rightarrow \text{M}_{n}(\text{F})$
and a principal order
![]() $\mathfrak{a}\text{sp}\prime$
. This gives us a maximal simple character
$\mathfrak{a}\text{sp}\prime$
. This gives us a maximal simple character
![]() $\unicode[STIX]{x1D703}\text{sp}\prime$
, which is the transfer of
$\unicode[STIX]{x1D703}\text{sp}\prime$
, which is the transfer of
![]() $\unicode[STIX]{x1D703}$
in the sense of [Reference SécherreSéc04, § 3.3.3]. Let
$\unicode[STIX]{x1D703}$
in the sense of [Reference SécherreSéc04, § 3.3.3]. Let
![]() $\unicode[STIX]{x1D705}\text{sp}\prime$
be its unique
$\unicode[STIX]{x1D705}\text{sp}\prime$
be its unique
![]() $\unicode[STIX]{x1D6FD}$
-extension whose determinant has order a power of
$\unicode[STIX]{x1D6FD}$
-extension whose determinant has order a power of
![]() $p$
. This gives us a bijection
$p$
. This gives us a bijection
![]() $\text{X}/\unicode[STIX]{x1D6E4}\rightarrow \mathscr{D}_{0}(\text{H},\boldsymbol{\unicode[STIX]{x1D6E9}})$
, denoted by
$\text{X}/\unicode[STIX]{x1D6E4}\rightarrow \mathscr{D}_{0}(\text{H},\boldsymbol{\unicode[STIX]{x1D6E9}})$
, denoted by
![]() $\boldsymbol{\unicode[STIX]{x1D714}}\text{sp}\prime$
. Putting the bijections
$\boldsymbol{\unicode[STIX]{x1D714}}\text{sp}\prime$
. Putting the bijections
![]() $\boldsymbol{\unicode[STIX]{x1D714}}$
and
$\boldsymbol{\unicode[STIX]{x1D714}}$
and
![]() $\boldsymbol{\unicode[STIX]{x1D714}}\text{sp}\prime$
and the inertial Jacquet–Langlands correspondence
$\boldsymbol{\unicode[STIX]{x1D714}}\text{sp}\prime$
and the inertial Jacquet–Langlands correspondence
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}_{0}$
of (8.1) together, we get a permutation
$\boldsymbol{\unicode[STIX]{x1D70B}}_{0}$
of (8.1) together, we get a permutation
![]() $\unicode[STIX]{x1D6F6}=\boldsymbol{\unicode[STIX]{x1D714}}\text{sp}\prime ^{-1}\circ \boldsymbol{\unicode[STIX]{x1D70B}}_{0}\circ \boldsymbol{\unicode[STIX]{x1D714}}$
of
$\unicode[STIX]{x1D6F6}=\boldsymbol{\unicode[STIX]{x1D714}}\text{sp}\prime ^{-1}\circ \boldsymbol{\unicode[STIX]{x1D70B}}_{0}\circ \boldsymbol{\unicode[STIX]{x1D714}}$
of
![]() $\text{X}/\unicode[STIX]{x1D6E4}$
.
$\text{X}/\unicode[STIX]{x1D6E4}$
.
Remark 9.1. This permutation depends a priori on the choice of the ps-character
![]() $(\unicode[STIX]{x1D6E9},0,\unicode[STIX]{x1D6FD})$
with endo-class
$(\unicode[STIX]{x1D6E9},0,\unicode[STIX]{x1D6FD})$
with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
, as well as on that of
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
, as well as on that of
![]() $\unicode[STIX]{x1D704},\mathfrak{a},\unicode[STIX]{x1D704}\text{sp}\prime ,\mathfrak{a}\text{sp}\prime$
. Under the Compatibility Assumption below, Theorem 9.3 will show that
$\unicode[STIX]{x1D704},\mathfrak{a},\unicode[STIX]{x1D704}\text{sp}\prime ,\mathfrak{a}\text{sp}\prime$
. Under the Compatibility Assumption below, Theorem 9.3 will show that
![]() $\unicode[STIX]{x1D6F6}$
is actually independent of these choices.
$\unicode[STIX]{x1D6F6}$
is actually independent of these choices.
We now go back to the simple character
![]() $\unicode[STIX]{x1D703}$
. Restricting it to the
$\unicode[STIX]{x1D703}$
. Restricting it to the
![]() $1$
-units of
$1$
-units of
![]() $\mathfrak{b}$
, it takes the form
$\mathfrak{b}$
, it takes the form
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D703}}\circ \text{Nrd}_{\text{B}}$
for a unique character
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D703}}\circ \text{Nrd}_{\text{B}}$
for a unique character
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D703}}$
of the
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D703}}$
of the
![]() $1$
-units
$1$
-units
![]() $1+\mathfrak{p}_{\unicode[STIX]{x1D704}\text{E}}$
, where
$1+\mathfrak{p}_{\unicode[STIX]{x1D704}\text{E}}$
, where
![]() $\text{Nrd}_{\text{B}}$
denotes the reduced norm of
$\text{Nrd}_{\text{B}}$
denotes the reduced norm of
![]() $\text{B}$
(see [Reference SécherreSéc04, 3.3.2]). Composing with
$\text{B}$
(see [Reference SécherreSéc04, 3.3.2]). Composing with
![]() $\unicode[STIX]{x1D704}$
, we get a character
$\unicode[STIX]{x1D704}$
, we get a character
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D703}}\,\circ \,\unicode[STIX]{x1D704}$
of
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D703}}\,\circ \,\unicode[STIX]{x1D704}$
of
![]() $1+\mathfrak{p}_{\text{E}}$
. Similarly, we have a character
$1+\mathfrak{p}_{\text{E}}$
. Similarly, we have a character
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D703}\text{sp}\prime }\,\circ \,\unicode[STIX]{x1D704}\text{sp}\prime$
of the same group.
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D703}\text{sp}\prime }\,\circ \,\unicode[STIX]{x1D704}\text{sp}\prime$
of the same group.
Compatibility Assumption. We assume that
on
![]() $1+\mathfrak{p}_{\text{E}}$
.
$1+\mathfrak{p}_{\text{E}}$
.
From now on, we assume that the Compatibility Assumption is satisfied. The character (9.2) of the
![]() $1$
-units
$1$
-units
![]() $1+\mathfrak{p}_{\text{E}}$
will be denoted by
$1+\mathfrak{p}_{\text{E}}$
will be denoted by
![]() $\unicode[STIX]{x1D709}_{0}$
.
$\unicode[STIX]{x1D709}_{0}$
.
Remark 9.2. Let
![]() $\mathscr{E}(\text{F})$
denote the set of all endo-classes over
$\mathscr{E}(\text{F})$
denote the set of all endo-classes over
![]() $\text{F}$
, and define
$\text{F}$
, and define
![]() $\mathscr{E}(\text{E})$
accordingly. There is a canonical map
$\mathscr{E}(\text{E})$
accordingly. There is a canonical map
given by [Reference Bushnell and HenniartBH96, Corollary 9.3] (see also [Reference Bushnell and HenniartBH14, ch. 2]), called the restriction map. It is surjective with finite fibres. According to [Reference Bushnell and HenniartBH05b, § 1.2], we can identify
![]() $\text{E}$
-endo-classes of degree
$\text{E}$
-endo-classes of degree
![]() $1$
with characters of
$1$
with characters of
![]() $1+\mathfrak{p}_{\text{E}}$
. The tameness assumption on
$1+\mathfrak{p}_{\text{E}}$
. The tameness assumption on
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
implies that the
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
implies that the
![]() $\text{E}/\text{F}$
-lifts of
$\text{E}/\text{F}$
-lifts of
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
, that is, the endo-classes in
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
, that is, the endo-classes in
![]() $\mathscr{E}(\text{E})$
whose restriction to
$\mathscr{E}(\text{E})$
whose restriction to
![]() $\mathscr{E}(\text{F})$
is
$\mathscr{E}(\text{F})$
is
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
, all have degree
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
, all have degree
![]() $1$
. Besides,
$1$
. Besides,
![]() $\unicode[STIX]{x1D709}_{0}$
is one of these lifts, and the map
$\unicode[STIX]{x1D709}_{0}$
is one of these lifts, and the map
![]() $\unicode[STIX]{x1D6FE}\mapsto \unicode[STIX]{x1D709}_{0}\circ \unicode[STIX]{x1D6FE}$
induces a bijection between
$\unicode[STIX]{x1D6FE}\mapsto \unicode[STIX]{x1D709}_{0}\circ \unicode[STIX]{x1D6FE}$
induces a bijection between
![]() $\text{Aut}_{\text{F}}(\text{E})$
and the set of
$\text{Aut}_{\text{F}}(\text{E})$
and the set of
![]() $\text{E}/\text{F}$
-lifts of
$\text{E}/\text{F}$
-lifts of
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
(see [Reference Bushnell and HenniartBH14, Corollary 2.4])). This gives us a full description of the
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
(see [Reference Bushnell and HenniartBH14, Corollary 2.4])). This gives us a full description of the
![]() $\text{E}/\text{F}$
-lifts of
$\text{E}/\text{F}$
-lifts of
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
.
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
.
Our purpose is to get a formula for
![]() $\unicode[STIX]{x1D6F6}$
. In § 9.4, we will use the results of [Reference Bushnell and HenniartBH11a] to compute the
$\unicode[STIX]{x1D6F6}$
. In § 9.4, we will use the results of [Reference Bushnell and HenniartBH11a] to compute the
![]() $\unicode[STIX]{x1D6E4}$
-orbit
$\unicode[STIX]{x1D6E4}$
-orbit
![]() $\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FC}])$
for
$\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FC}])$
for
![]() $\boldsymbol{e}$
-regular characters
$\boldsymbol{e}$
-regular characters
![]() $\unicode[STIX]{x1D6FC}\in \text{X}$
. We will then use Proposition 8.8 to extend this formula to all characters
$\unicode[STIX]{x1D6FC}\in \text{X}$
. We will then use Proposition 8.8 to extend this formula to all characters
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.
Theorem 9.3. There is a canonically determined character
![]() $\unicode[STIX]{x1D707}$
of
$\unicode[STIX]{x1D707}$
of
![]() $\boldsymbol{k}^{\times }$
, depending only on
$\boldsymbol{k}^{\times }$
, depending only on
![]() $m$
,
$m$
,
![]() $d$
and
$d$
and
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
, such that
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
, such that
![]() $\unicode[STIX]{x1D707}^{2}=1$
and
$\unicode[STIX]{x1D707}^{2}=1$
and
for all characters
![]() $\unicode[STIX]{x1D6FC}\in \text{X}$
.
$\unicode[STIX]{x1D6FC}\in \text{X}$
.
More precisely, we will see that the character
![]() $\unicode[STIX]{x1D707}$
is the ‘rectifier’ given by Bushnell and Henniart’s First Comparison Theorem [Reference Bushnell and HenniartBH11a, 6.1] together with Corollary 6.9 and (6.7.4) in [Reference Bushnell and HenniartBH11a]. Since the results from [Reference Bushnell and HenniartBH11a] we will use are formulated in terms of admissible pairs, we first have to translate them in terms of our
$\unicode[STIX]{x1D707}$
is the ‘rectifier’ given by Bushnell and Henniart’s First Comparison Theorem [Reference Bushnell and HenniartBH11a, 6.1] together with Corollary 6.9 and (6.7.4) in [Reference Bushnell and HenniartBH11a]. Since the results from [Reference Bushnell and HenniartBH11a] we will use are formulated in terms of admissible pairs, we first have to translate them in terms of our
![]() $\unicode[STIX]{x1D6FC}$
-parameters.
$\unicode[STIX]{x1D6FC}$
-parameters.
Let us write
![]() $\text{X}_{\text{reg}}$
for the set of
$\text{X}_{\text{reg}}$
for the set of
![]() $\boldsymbol{e}$
-regular characters in
$\boldsymbol{e}$
-regular characters in
![]() $\text{X}$
.
$\text{X}$
.
9.2
We first recall the definition of admissible pairs [Reference HoweHow77, Reference Bushnell and HenniartBH11a], and basic facts about them.
Definition 9.4. An admissible pair is a pair
![]() $(\text{L}/\text{F},\unicode[STIX]{x1D709})$
consisting of a finite, tamely ramified field extension
$(\text{L}/\text{F},\unicode[STIX]{x1D709})$
consisting of a finite, tamely ramified field extension
![]() $\text{L}/\text{F}$
and a character
$\text{L}/\text{F}$
and a character
![]() $\unicode[STIX]{x1D709}$
of
$\unicode[STIX]{x1D709}$
of
![]() $\text{L}^{\times }$
such that:
$\text{L}^{\times }$
such that:
(1)
 $\unicode[STIX]{x1D709}$
does not factor through
$\unicode[STIX]{x1D709}$
does not factor through
 $\text{N}_{\text{L}/\text{K}}$
for any field
$\text{N}_{\text{L}/\text{K}}$
for any field
 $\text{K}$
such that
$\text{K}$
such that
 $\text{F}\subseteq \text{K}\subsetneq \text{L}$
;
$\text{F}\subseteq \text{K}\subsetneq \text{L}$
;(2) if the restriction of
 $\unicode[STIX]{x1D709}$
to the
$\unicode[STIX]{x1D709}$
to the
 $1$
-units
$1$
-units
 $1+\mathfrak{p}_{\text{L}}$
factors through
$1+\mathfrak{p}_{\text{L}}$
factors through
 $\text{N}_{\text{L}/\text{K}}$
for some field
$\text{N}_{\text{L}/\text{K}}$
for some field
 $\text{K}$
such that
$\text{K}$
such that
 $\text{F}\subseteq \text{K}\subseteq \text{L}$
, then
$\text{F}\subseteq \text{K}\subseteq \text{L}$
, then
 $\text{L}/\text{K}$
is unramified.
$\text{L}/\text{K}$
is unramified.
Two admissible pairs
![]() $(\text{L}_{i}/\text{F},\unicode[STIX]{x1D709}_{i})$
,
$(\text{L}_{i}/\text{F},\unicode[STIX]{x1D709}_{i})$
,
![]() $i=1,2$
, are said to be isomorphic if there is an
$i=1,2$
, are said to be isomorphic if there is an
![]() $\text{F}$
-isomorphism
$\text{F}$
-isomorphism
![]() $\unicode[STIX]{x1D719}:\text{L}_{2}\rightarrow \text{L}_{1}$
such that
$\unicode[STIX]{x1D719}:\text{L}_{2}\rightarrow \text{L}_{1}$
such that
![]() $\unicode[STIX]{x1D709}_{2}=\unicode[STIX]{x1D709}_{1}\circ \unicode[STIX]{x1D719}$
. The degree of an admissible pair
$\unicode[STIX]{x1D709}_{2}=\unicode[STIX]{x1D709}_{1}\circ \unicode[STIX]{x1D719}$
. The degree of an admissible pair
![]() $(\text{L}/\text{F},\unicode[STIX]{x1D709})$
is
$(\text{L}/\text{F},\unicode[STIX]{x1D709})$
is
![]() $[\text{L}:\text{F}]$
. We also introduce the following definition, which will be convenient for our use.
$[\text{L}:\text{F}]$
. We also introduce the following definition, which will be convenient for our use.
Definition 9.5. Two admissible pairs
![]() $(\text{L}_{i}/\text{F},\unicode[STIX]{x1D709}_{i})$
for
$(\text{L}_{i}/\text{F},\unicode[STIX]{x1D709}_{i})$
for
![]() $i=1,2$
, are said to be inertially equivalent if there exist an unramified character
$i=1,2$
, are said to be inertially equivalent if there exist an unramified character
![]() $\unicode[STIX]{x1D712}$
of
$\unicode[STIX]{x1D712}$
of
![]() $\text{L}_{2}^{\times }$
and an isomorphism
$\text{L}_{2}^{\times }$
and an isomorphism
![]() $\unicode[STIX]{x1D719}:\text{L}_{2}\rightarrow \text{L}_{1}$
of extensions of
$\unicode[STIX]{x1D719}:\text{L}_{2}\rightarrow \text{L}_{1}$
of extensions of
![]() $\text{F}$
such that
$\text{F}$
such that
![]() $\unicode[STIX]{x1D712}\unicode[STIX]{x1D709}_{2}=\unicode[STIX]{x1D709}_{1}\circ \unicode[STIX]{x1D719}$
. We will write
$\unicode[STIX]{x1D712}\unicode[STIX]{x1D709}_{2}=\unicode[STIX]{x1D709}_{1}\circ \unicode[STIX]{x1D719}$
. We will write
![]() $[\text{L}_{1}/\text{F},\unicode[STIX]{x1D709}_{1}]$
for the inertial class of
$[\text{L}_{1}/\text{F},\unicode[STIX]{x1D709}_{1}]$
for the inertial class of
![]() $(\text{L}_{1}/\text{F},\unicode[STIX]{x1D709}_{1})$
.
$(\text{L}_{1}/\text{F},\unicode[STIX]{x1D709}_{1})$
.
Let
![]() $(\text{L}/\text{F},\unicode[STIX]{x1D709})$
be an admissible pair. By [Reference Bushnell and HenniartBH11a, 4.1 Lemma], there is a unique sub-extension
$(\text{L}/\text{F},\unicode[STIX]{x1D709})$
be an admissible pair. By [Reference Bushnell and HenniartBH11a, 4.1 Lemma], there is a unique sub-extension
![]() $\text{P}/\text{F}$
of
$\text{P}/\text{F}$
of
![]() $\text{L}/\text{F}$
such that
$\text{L}/\text{F}$
such that
![]() $\unicode[STIX]{x1D709}~|~1+\mathfrak{p}_{\text{L}}$
factors through the norm
$\unicode[STIX]{x1D709}~|~1+\mathfrak{p}_{\text{L}}$
factors through the norm
![]() $\text{N}_{\text{L}/\text{P}}$
and which is minimal for this property. It is called the parameter field of the admissible pair. Then
$\text{N}_{\text{L}/\text{P}}$
and which is minimal for this property. It is called the parameter field of the admissible pair. Then
![]() $\text{L}/\text{P}$
is unramified and, if we write
$\text{L}/\text{P}$
is unramified and, if we write
![]() $\unicode[STIX]{x1D709}~|~1+\mathfrak{p}_{\text{L}}=\unicode[STIX]{x1D709}_{1}\circ \text{N}_{\text{L}/\text{P}}$
for some character
$\unicode[STIX]{x1D709}~|~1+\mathfrak{p}_{\text{L}}=\unicode[STIX]{x1D709}_{1}\circ \text{N}_{\text{L}/\text{P}}$
for some character
![]() $\unicode[STIX]{x1D709}_{1}$
of
$\unicode[STIX]{x1D709}_{1}$
of
![]() $1+\mathfrak{p}_{\text{P}}$
, then
$1+\mathfrak{p}_{\text{P}}$
, then
![]() $(\text{P}/\text{F},\unicode[STIX]{x1D709}_{1})$
is an admissible
$(\text{P}/\text{F},\unicode[STIX]{x1D709}_{1})$
is an admissible
![]() $1$
-pair in the sense of [Reference Bushnell and HenniartBH11a, 3.3], that is,
$1$
-pair in the sense of [Reference Bushnell and HenniartBH11a, 3.3], that is,
![]() $\unicode[STIX]{x1D709}_{1}$
does not factor through
$\unicode[STIX]{x1D709}_{1}$
does not factor through
![]() $\text{N}_{\text{L}/\text{K}}$
for any field
$\text{N}_{\text{L}/\text{K}}$
for any field
![]() $\text{K}$
such that
$\text{K}$
such that
![]() $\text{F}\subseteq \text{K}\subsetneq \text{L}$
. According to [Reference Bushnell and HenniartBH05b, Theorem 1.3], there is a canonical bijective map between isomorphism classes of admissible
$\text{F}\subseteq \text{K}\subsetneq \text{L}$
. According to [Reference Bushnell and HenniartBH05b, Theorem 1.3], there is a canonical bijective map between isomorphism classes of admissible
![]() $1$
-pairs over
$1$
-pairs over
![]() $\text{F}$
and essentially tame endo-classes over
$\text{F}$
and essentially tame endo-classes over
![]() $\text{F}$
. Therefore, the admissible
$\text{F}$
. Therefore, the admissible
![]() $1$
-pair
$1$
-pair
![]() $(\text{P}/\text{F},\unicode[STIX]{x1D709}_{1})$
determines an essentially tame endo-class, which depends on the inertial class of
$(\text{P}/\text{F},\unicode[STIX]{x1D709}_{1})$
determines an essentially tame endo-class, which depends on the inertial class of
![]() $(\text{L}/\text{F},\unicode[STIX]{x1D709})$
only.
$(\text{L}/\text{F},\unicode[STIX]{x1D709})$
only.
Recall that we have fixed an endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
and a character
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
and a character
![]() $\unicode[STIX]{x1D709}_{0}$
of
$\unicode[STIX]{x1D709}_{0}$
of
![]() $1+\mathfrak{p}_{\text{E}}$
in the Compatibility Assumption of § 9.1.
$1+\mathfrak{p}_{\text{E}}$
in the Compatibility Assumption of § 9.1.
Lemma 9.6. Any admissible pair having endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
is isomorphic to an admissible pair
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
is isomorphic to an admissible pair
![]() $(\text{L}/\text{F},\unicode[STIX]{x1D709})$
with associated
$(\text{L}/\text{F},\unicode[STIX]{x1D709})$
with associated
![]() $1$
-pair
$1$
-pair
![]() $(\text{E}/\text{F},\unicode[STIX]{x1D709}_{0})$
.
$(\text{E}/\text{F},\unicode[STIX]{x1D709}_{0})$
.
Proof. Suppose that
![]() $(\text{L}/\text{F},\unicode[STIX]{x1D709})$
has endo-class
$(\text{L}/\text{F},\unicode[STIX]{x1D709})$
has endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
, and let
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
, and let
![]() $(\text{P}/\text{F},\unicode[STIX]{x1D709}_{1})$
be its associated admissible
$(\text{P}/\text{F},\unicode[STIX]{x1D709}_{1})$
be its associated admissible
![]() $1$
-pair. By looking at [Reference Bushnell and HenniartBH05b, § 1.3] in more detail, it follows that
$1$
-pair. By looking at [Reference Bushnell and HenniartBH05b, § 1.3] in more detail, it follows that
![]() $\text{P}$
is
$\text{P}$
is
![]() $\text{F}$
-isomorphic to
$\text{F}$
-isomorphic to
![]() $\text{E}$
. Up to isomorphism, we may therefore assume that
$\text{E}$
. Up to isomorphism, we may therefore assume that
![]() $\text{P}$
is equal to
$\text{P}$
is equal to
![]() $\text{E}$
. By Remark 9.2, the characters
$\text{E}$
. By Remark 9.2, the characters
![]() $\unicode[STIX]{x1D709}_{1}$
and
$\unicode[STIX]{x1D709}_{1}$
and
![]() $\unicode[STIX]{x1D709}_{0}$
of
$\unicode[STIX]{x1D709}_{0}$
of
![]() $1+\mathfrak{p}_{\text{E}}$
, which define the same endo-class
$1+\mathfrak{p}_{\text{E}}$
, which define the same endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
, are conjugate under the automorphism group
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
, are conjugate under the automorphism group
![]() $\text{Aut}_{\text{F}}(\text{E})$
. Therefore, up to isomorphism, we may assume that these characters
$\text{Aut}_{\text{F}}(\text{E})$
. Therefore, up to isomorphism, we may assume that these characters
![]() $\unicode[STIX]{x1D709}_{1}$
and
$\unicode[STIX]{x1D709}_{1}$
and
![]() $\unicode[STIX]{x1D709}_{0}$
are equal.◻
$\unicode[STIX]{x1D709}_{0}$
are equal.◻
9.3
Let
![]() $(\text{L}/\text{F},\unicode[STIX]{x1D709})$
be an admissible pair with endo-class
$(\text{L}/\text{F},\unicode[STIX]{x1D709})$
be an admissible pair with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
and degree
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
and degree
![]() $t$
dividing
$t$
dividing
![]() $n$
. By Lemma 9.6, we may assume that it has associated
$n$
. By Lemma 9.6, we may assume that it has associated
![]() $1$
-pair
$1$
-pair
![]() $(\text{E}/\text{F},\unicode[STIX]{x1D709}_{0})$
. We may also assume that
$(\text{E}/\text{F},\unicode[STIX]{x1D709}_{0})$
. We may also assume that
![]() $\text{L}$
is contained in
$\text{L}$
is contained in
![]() $\overline{\text{F}}$
. By [Reference Bushnell and HenniartBH11a, 4.3 Lemma 1], there is a unique character
$\overline{\text{F}}$
. By [Reference Bushnell and HenniartBH11a, 4.3 Lemma 1], there is a unique character
![]() $\unicode[STIX]{x1D709}_{\text{w}}$
of the group of units
$\unicode[STIX]{x1D709}_{\text{w}}$
of the group of units
![]() $\mathscr{O}_{\text{L}}^{\times }$
such that:
$\mathscr{O}_{\text{L}}^{\times }$
such that:
(1) the characters
 $\unicode[STIX]{x1D709}_{\text{w}}$
and
$\unicode[STIX]{x1D709}_{\text{w}}$
and
 $\unicode[STIX]{x1D709}$
coincide on the principal unit subgroup
$\unicode[STIX]{x1D709}$
coincide on the principal unit subgroup
 $1+\mathfrak{p}_{\text{L}}$
;
$1+\mathfrak{p}_{\text{L}}$
;(2) the order of
 $\unicode[STIX]{x1D709}_{\text{w}}$
is a power of
$\unicode[STIX]{x1D709}_{\text{w}}$
is a power of
 $p$
.
$p$
.
The character
![]() $\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}_{\text{w}}^{-1}$
of
$\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}_{\text{w}}^{-1}$
of
![]() $\mathscr{O}_{\text{L}}^{\times }$
is tamely ramified; thus it induces a character
$\mathscr{O}_{\text{L}}^{\times }$
is tamely ramified; thus it induces a character
![]() $\unicode[STIX]{x1D709}_{\text{t}}$
of
$\unicode[STIX]{x1D709}_{\text{t}}$
of
![]() $\boldsymbol{l}^{\times }$
, where
$\boldsymbol{l}^{\times }$
, where
![]() $\boldsymbol{l}$
is the residue field of
$\boldsymbol{l}$
is the residue field of
![]() $\text{L}$
. This character depends only on the inertial class of
$\text{L}$
. This character depends only on the inertial class of
![]() $(\text{L}/\text{F},\unicode[STIX]{x1D709})$
.
$(\text{L}/\text{F},\unicode[STIX]{x1D709})$
.
Since
![]() $(\text{L}/\text{F},\unicode[STIX]{x1D709})$
is an admissible pair with parameter field
$(\text{L}/\text{F},\unicode[STIX]{x1D709})$
is an admissible pair with parameter field
![]() $\text{E}$
, the residue field
$\text{E}$
, the residue field
![]() $\boldsymbol{l}$
is an extension of
$\boldsymbol{l}$
is an extension of
![]() $\boldsymbol{e}$
and
$\boldsymbol{e}$
and
![]() $\unicode[STIX]{x1D709}_{\text{t}}$
is an
$\unicode[STIX]{x1D709}_{\text{t}}$
is an
![]() $\boldsymbol{e}$
-regular character of
$\boldsymbol{e}$
-regular character of
![]() $\boldsymbol{l}^{\times }$
. Since
$\boldsymbol{l}^{\times }$
. Since
![]() $\text{L}\subseteq \overline{\text{F}}$
, the residue field
$\text{L}\subseteq \overline{\text{F}}$
, the residue field
![]() $\boldsymbol{l}$
naturally embeds in
$\boldsymbol{l}$
naturally embeds in
![]() $\boldsymbol{k}$
. Write
$\boldsymbol{k}$
. Write
![]() $\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D709}}$
for the character
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D709}}$
for the character
![]() $\unicode[STIX]{x1D709}_{\text{t}}\circ \text{N}_{\boldsymbol{k}/\boldsymbol{l}}$
of
$\unicode[STIX]{x1D709}_{\text{t}}\circ \text{N}_{\boldsymbol{k}/\boldsymbol{l}}$
of
![]() $\boldsymbol{k}^{\times }$
. Its parametric degree
$\boldsymbol{k}^{\times }$
. Its parametric degree
![]() $f$
is equal to
$f$
is equal to
![]() $[\text{L}:\text{E}]$
. We thus have
$[\text{L}:\text{E}]$
. We thus have
![]() $t=fg$
.
$t=fg$
.
We write
![]() $\mathscr{P}_{n}(\boldsymbol{\unicode[STIX]{x1D6E9}})$
for the set of inertial classes of admissible pairs with endo-class
$\mathscr{P}_{n}(\boldsymbol{\unicode[STIX]{x1D6E9}})$
for the set of inertial classes of admissible pairs with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
and degree dividing
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
and degree dividing
![]() $n$
.
$n$
.
Lemma 9.7.
![]() $(1)$
The character
$(1)$
The character
![]() $\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D709}}$
is
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D709}}$
is
![]() $\boldsymbol{e}$
-regular if and only if
$\boldsymbol{e}$
-regular if and only if
![]() $[\text{L}:\text{F}]=n$
.
$[\text{L}:\text{F}]=n$
.
![]() $(2)$
The map
$(2)$
The map
induces a bijection between the set of inertial classes of admissible pairs in
![]() $\mathscr{P}_{n}(\boldsymbol{\unicode[STIX]{x1D6E9}})$
and
$\mathscr{P}_{n}(\boldsymbol{\unicode[STIX]{x1D6E9}})$
and
![]() $\text{X}/\unicode[STIX]{x1D6E4}$
.
$\text{X}/\unicode[STIX]{x1D6E4}$
.
Proof. The character
![]() $\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D709}}$
is
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D709}}$
is
![]() $\boldsymbol{e}$
-regular if and only if
$\boldsymbol{e}$
-regular if and only if
![]() $f=n\text{sp}\prime$
. Multiplying by
$f=n\text{sp}\prime$
. Multiplying by
![]() $g$
, this is equivalent to
$g$
, this is equivalent to
![]() $t=n$
. This gives us the first part of the lemma.
$t=n$
. This gives us the first part of the lemma.
Given
![]() $\unicode[STIX]{x1D6FC}\in \text{X}$
, there is a uniquely determined field
$\unicode[STIX]{x1D6FC}\in \text{X}$
, there is a uniquely determined field
![]() $\boldsymbol{l}$
such that
$\boldsymbol{l}$
such that
![]() $\boldsymbol{e}\subseteq \boldsymbol{l}\subseteq \boldsymbol{k}$
and
$\boldsymbol{e}\subseteq \boldsymbol{l}\subseteq \boldsymbol{k}$
and
![]() $\unicode[STIX]{x1D6FC}$
factors through the norm
$\unicode[STIX]{x1D6FC}$
factors through the norm
![]() $\text{N}_{\boldsymbol{k}/\boldsymbol{l}}$
, and which is minimal for this property. Write
$\text{N}_{\boldsymbol{k}/\boldsymbol{l}}$
, and which is minimal for this property. Write
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}\circ \text{N}_{\boldsymbol{k}/\boldsymbol{l}}$
for some character
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}\circ \text{N}_{\boldsymbol{k}/\boldsymbol{l}}$
for some character
![]() $\unicode[STIX]{x1D6FD}$
of
$\unicode[STIX]{x1D6FD}$
of
![]() $\boldsymbol{l}^{\times }$
, which is
$\boldsymbol{l}^{\times }$
, which is
![]() $\boldsymbol{e}$
-regular by minimality of
$\boldsymbol{e}$
-regular by minimality of
![]() $\boldsymbol{l}$
. Let
$\boldsymbol{l}$
. Let
![]() $\text{L}$
be an unramified extension of
$\text{L}$
be an unramified extension of
![]() $\text{E}$
with residue field
$\text{E}$
with residue field
![]() $\boldsymbol{l}$
. Then
$\boldsymbol{l}$
. Then
![]() $\unicode[STIX]{x1D6FD}$
inflates to a tamely ramified character of the units subgroup of
$\unicode[STIX]{x1D6FD}$
inflates to a tamely ramified character of the units subgroup of
![]() $\text{L}$
, still denoted by
$\text{L}$
, still denoted by
![]() $\unicode[STIX]{x1D6FD}$
. Now write
$\unicode[STIX]{x1D6FD}$
. Now write
![]() $\unicode[STIX]{x1D709}_{\text{w}}$
for the character of
$\unicode[STIX]{x1D709}_{\text{w}}$
for the character of
![]() $\mathscr{O}_{\text{L}}^{\times }$
of
$\mathscr{O}_{\text{L}}^{\times }$
of
![]() $p$
-power order extending the character
$p$
-power order extending the character
![]() $\unicode[STIX]{x1D709}_{0}\circ \text{N}_{\text{L}/\text{E}}$
of the
$\unicode[STIX]{x1D709}_{0}\circ \text{N}_{\text{L}/\text{E}}$
of the
![]() $1$
-units of
$1$
-units of
![]() $\text{L}$
, and let
$\text{L}$
, and let
![]() $\unicode[STIX]{x1D709}$
be any character of
$\unicode[STIX]{x1D709}$
be any character of
![]() $\text{L}^{\times }$
extending
$\text{L}^{\times }$
extending
![]() $\unicode[STIX]{x1D709}_{\text{w}}\unicode[STIX]{x1D6FD}$
. Since the character
$\unicode[STIX]{x1D709}_{\text{w}}\unicode[STIX]{x1D6FD}$
. Since the character
![]() $\unicode[STIX]{x1D6FD}$
is
$\unicode[STIX]{x1D6FD}$
is
![]() $\boldsymbol{e}$
-regular, it follows that the pair
$\boldsymbol{e}$
-regular, it follows that the pair
![]() $(\text{L}/\text{F},\unicode[STIX]{x1D709})$
is admissible. The
$(\text{L}/\text{F},\unicode[STIX]{x1D709})$
is admissible. The
![]() $\unicode[STIX]{x1D6E4}$
-orbit
$\unicode[STIX]{x1D6E4}$
-orbit
![]() $[\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D709}}]$
associated with its inertial class is equal to
$[\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D709}}]$
associated with its inertial class is equal to
![]() $[\unicode[STIX]{x1D6FC}]$
. The map (9.3) is therefore surjective.
$[\unicode[STIX]{x1D6FC}]$
. The map (9.3) is therefore surjective.
We now assume that we have two admissible pairs
![]() $(\text{L}_{i}/\text{F},\unicode[STIX]{x1D709}_{i})$
for
$(\text{L}_{i}/\text{F},\unicode[STIX]{x1D709}_{i})$
for
![]() $i=1,2$
, with the same image
$i=1,2$
, with the same image
![]() $[\unicode[STIX]{x1D6FC}]$
in
$[\unicode[STIX]{x1D6FC}]$
in
![]() $\text{X}/\unicode[STIX]{x1D6E4}$
. For each
$\text{X}/\unicode[STIX]{x1D6E4}$
. For each
![]() $i$
, we may assume that
$i$
, we may assume that
![]() $(\text{L}_{i}/\text{F},\unicode[STIX]{x1D709}_{i})$
has associated
$(\text{L}_{i}/\text{F},\unicode[STIX]{x1D709}_{i})$
has associated
![]() $1$
-pair
$1$
-pair
![]() $(\text{E}/\text{F},\unicode[STIX]{x1D709}_{0})$
by Lemma 9.6, and we may further assume that
$(\text{E}/\text{F},\unicode[STIX]{x1D709}_{0})$
by Lemma 9.6, and we may further assume that
![]() $\text{L}_{i}\subseteq \overline{\text{F}}$
. The character
$\text{L}_{i}\subseteq \overline{\text{F}}$
. The character
![]() $\unicode[STIX]{x1D709}_{i}~|~1\,+\,\mathfrak{p}_{\text{L}_{i}}$
thus factors through
$\unicode[STIX]{x1D709}_{i}~|~1\,+\,\mathfrak{p}_{\text{L}_{i}}$
thus factors through
![]() $\text{N}_{\text{L}_{i}/\text{E}}$
and
$\text{N}_{\text{L}_{i}/\text{E}}$
and
![]() $\text{E}$
is minimal for this property. We have an
$\text{E}$
is minimal for this property. We have an
![]() $\boldsymbol{e}$
-regular character
$\boldsymbol{e}$
-regular character
![]() $\unicode[STIX]{x1D709}_{i,\text{t}}$
of
$\unicode[STIX]{x1D709}_{i,\text{t}}$
of
![]() $\boldsymbol{l}_{i}^{\times }$
, where
$\boldsymbol{l}_{i}^{\times }$
, where
![]() $\boldsymbol{l}_{i}$
is the residue field of
$\boldsymbol{l}_{i}$
is the residue field of
![]() $\text{L}_{i}$
. Since
$\text{L}_{i}$
. Since
![]() $[\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D709}_{1}}]$
and
$[\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D709}_{1}}]$
and
![]() $[\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D709}_{2}}]$
are equal, they have the same cardinality
$[\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D709}_{2}}]$
are equal, they have the same cardinality
![]() $f$
. The fields
$f$
. The fields
![]() $\boldsymbol{l}_{1}$
and
$\boldsymbol{l}_{1}$
and
![]() $\boldsymbol{l}_{2}$
therefore have the same degree over
$\boldsymbol{l}_{2}$
therefore have the same degree over
![]() $\boldsymbol{e}$
, and
$\boldsymbol{e}$
, and
![]() $\text{L}_{1}$
and
$\text{L}_{1}$
and
![]() $\text{L}_{2}$
have the same degree
$\text{L}_{2}$
have the same degree
![]() $f$
over
$f$
over
![]() $\text{E}$
. We thus have
$\text{E}$
. We thus have
![]() $\text{L}_{1}=\text{L}_{2}$
, denoted by
$\text{L}_{1}=\text{L}_{2}$
, denoted by
![]() $\text{L}$
. We now have two characters
$\text{L}$
. We now have two characters
![]() $\unicode[STIX]{x1D709}_{1,\text{t}}$
and
$\unicode[STIX]{x1D709}_{1,\text{t}}$
and
![]() $\unicode[STIX]{x1D709}_{2,\text{t}}$
of
$\unicode[STIX]{x1D709}_{2,\text{t}}$
of
![]() $\boldsymbol{l}^{\times }$
, which are conjugate under
$\boldsymbol{l}^{\times }$
, which are conjugate under
![]() $\text{Gal}(\boldsymbol{l}/\boldsymbol{e})$
. Changing again
$\text{Gal}(\boldsymbol{l}/\boldsymbol{e})$
. Changing again
![]() $(\text{L}_{2}/\text{F},\unicode[STIX]{x1D709}_{2})$
in its isomorphism class, we may assume that they are equal. Thus the admissible pairs
$(\text{L}_{2}/\text{F},\unicode[STIX]{x1D709}_{2})$
in its isomorphism class, we may assume that they are equal. Thus the admissible pairs
![]() $(\text{L}_{i}/\text{F},\unicode[STIX]{x1D709}_{i})$
for
$(\text{L}_{i}/\text{F},\unicode[STIX]{x1D709}_{i})$
for
![]() $i=1,2$
, are inertially equivalent.◻
$i=1,2$
, are inertially equivalent.◻
9.4
The Parametrization Theorem in [Reference Bushnell and HenniartBH11a, 6.1] gives us a canonical bijection
between isomorphism classes of admissible pairs of degree
![]() $n$
and isomorphism classes of essentially tame irreducible cuspidal representations of
$n$
and isomorphism classes of essentially tame irreducible cuspidal representations of
![]() $\text{G}$
(that is, cuspidal representations with essentially tame endo-class) of parametric degree
$\text{G}$
(that is, cuspidal representations with essentially tame endo-class) of parametric degree
![]() $n$
.
$n$
.
Lemma 9.9.
![]() $(1)$
Given an admissible pair
$(1)$
Given an admissible pair
![]() $(\text{L}/\text{F},\unicode[STIX]{x1D709})$
of degree
$(\text{L}/\text{F},\unicode[STIX]{x1D709})$
of degree
![]() $n$
with associated
$n$
with associated
![]() $1$
-pair
$1$
-pair
![]() $(\text{E}/\text{F},\unicode[STIX]{x1D709}_{0})$
, the irreducible cuspidal representation
$(\text{E}/\text{F},\unicode[STIX]{x1D709}_{0})$
, the irreducible cuspidal representation
![]() $\unicode[STIX]{x1D6F1}(\text{G},\unicode[STIX]{x1D709})$
belongs to the inertial class
$\unicode[STIX]{x1D6F1}(\text{G},\unicode[STIX]{x1D709})$
belongs to the inertial class
![]() $\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D709}})$
.
$\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D709}})$
.
![]() $(2)$
The bijection (9.4) induces a bijection between inertial classes of admissible pairs of degree
$(2)$
The bijection (9.4) induces a bijection between inertial classes of admissible pairs of degree
![]() $n$
and inertial classes of essentially tame cuspidal representations of
$n$
and inertial classes of essentially tame cuspidal representations of
![]() $\text{G}$
of parametric degree
$\text{G}$
of parametric degree
![]() $n$
.
$n$
.
Proof. By examining the construction of [Reference Bushnell and HenniartBH11a, 4.2 and 4.3], we see that an essentially tame irreducible cuspidal representation of endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
will correspond through (9.4) to an admissible pair
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
will correspond through (9.4) to an admissible pair
![]() $(\text{L}/\text{F},\unicode[STIX]{x1D709})$
with associated
$(\text{L}/\text{F},\unicode[STIX]{x1D709})$
with associated
![]() $1$
-pair
$1$
-pair
![]() $(\text{E}/\text{F},\unicode[STIX]{x1D709}_{0})$
if and only if it contains the maximal simple type
$(\text{E}/\text{F},\unicode[STIX]{x1D709}_{0})$
if and only if it contains the maximal simple type
![]() $\unicode[STIX]{x1D705}\,\otimes \,\unicode[STIX]{x1D70E}$
, where
$\unicode[STIX]{x1D705}\,\otimes \,\unicode[STIX]{x1D70E}$
, where
![]() $\unicode[STIX]{x1D70E}$
is the irreducible cuspidal representation of
$\unicode[STIX]{x1D70E}$
is the irreducible cuspidal representation of
![]() $\mathscr{G}$
whose Green parameter in
$\mathscr{G}$
whose Green parameter in
![]() $\text{X}/\unicode[STIX]{x1D6E4}$
is
$\text{X}/\unicode[STIX]{x1D6E4}$
is
![]() $[\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D709}}]$
. Comparing with the construction of § 3.3, the simple type
$[\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D709}}]$
. Comparing with the construction of § 3.3, the simple type
![]() $\unicode[STIX]{x1D705}\,\otimes \,\unicode[STIX]{x1D70E}$
is
$\unicode[STIX]{x1D705}\,\otimes \,\unicode[STIX]{x1D70E}$
is
![]() $\boldsymbol{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D709}})$
. This gives us the first part of the lemma.
$\boldsymbol{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D709}})$
. This gives us the first part of the lemma.
An inertial class of essentially tame cuspidal representations of
![]() $\text{G}$
with endo-class
$\text{G}$
with endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
has the form
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
has the form
![]() $\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D6FC})$
for some
$\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D6FC})$
for some
![]() $\unicode[STIX]{x1D6FC}\in \text{X}_{\text{reg}}$
. The second part of the lemma thus follows from Lemma 9.7.◻
$\unicode[STIX]{x1D6FC}\in \text{X}_{\text{reg}}$
. The second part of the lemma thus follows from Lemma 9.7.◻
We now prove Theorem 9.3 for
![]() $\boldsymbol{e}$
-regular characters of
$\boldsymbol{e}$
-regular characters of
![]() $\text{X}$
.
$\text{X}$
.
Proposition 9.10.
![]() $(1)$
There is a canonically determined character
$(1)$
There is a canonically determined character
![]() $\unicode[STIX]{x1D707}\in \text{X}$
, depending on
$\unicode[STIX]{x1D707}\in \text{X}$
, depending on
![]() $m$
,
$m$
,
![]() $d$
and
$d$
and
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
only, such that
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
only, such that
![]() $\unicode[STIX]{x1D707}^{2}=1$
and
$\unicode[STIX]{x1D707}^{2}=1$
and
for all characters
![]() $\unicode[STIX]{x1D6FC}\in \text{X}_{\text{reg}}$
.
$\unicode[STIX]{x1D6FC}\in \text{X}_{\text{reg}}$
.
![]() $(2)$
The character
$(2)$
The character
![]() $\unicode[STIX]{x1D707}$
is non-trivial if and only if
$\unicode[STIX]{x1D707}$
is non-trivial if and only if
![]() $p\neq 2$
and the integer
$p\neq 2$
and the integer
is odd, where the integers
![]() $u,v\geqslant 1$
are defined by
$u,v\geqslant 1$
are defined by
![]() $uv=n/w$
and
$uv=n/w$
and
![]() $v=d/(d,w)$
with
$v=d/(d,w)$
with
![]() $w=n/e(\text{E}/\text{F})$
.
$w=n/e(\text{E}/\text{F})$
.
Proof. Let
![]() $\unicode[STIX]{x1D6FC}\in \text{X}_{\text{reg}}$
and let
$\unicode[STIX]{x1D6FC}\in \text{X}_{\text{reg}}$
and let
![]() $(\text{L}/\text{F},\unicode[STIX]{x1D709})$
be an admissible pair of degree
$(\text{L}/\text{F},\unicode[STIX]{x1D709})$
be an admissible pair of degree
![]() $n$
and endo-class
$n$
and endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
whose inertial class is associated with
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
whose inertial class is associated with
![]() $[\unicode[STIX]{x1D6FC}]$
. By [Reference Bushnell and HenniartBH11a, Theorem A], there is a tamely ramified character
$[\unicode[STIX]{x1D6FC}]$
. By [Reference Bushnell and HenniartBH11a, Theorem A], there is a tamely ramified character
![]() $\unicode[STIX]{x1D708}$
of
$\unicode[STIX]{x1D708}$
of
![]() $\text{L}^{\times }$
such that
$\text{L}^{\times }$
such that
![]() $(\text{L}/\text{F},\unicode[STIX]{x1D709}\unicode[STIX]{x1D708})$
is admissible,
$(\text{L}/\text{F},\unicode[STIX]{x1D709}\unicode[STIX]{x1D708})$
is admissible,
![]() $\unicode[STIX]{x1D708}^{2}$
is trivial and the Jacquet–Langlands transfer of
$\unicode[STIX]{x1D708}^{2}$
is trivial and the Jacquet–Langlands transfer of
![]() $\unicode[STIX]{x1D6F1}(\text{G},\unicode[STIX]{x1D709})$
is
$\unicode[STIX]{x1D6F1}(\text{G},\unicode[STIX]{x1D709})$
is
![]() $\unicode[STIX]{x1D6F1}(\text{H},\unicode[STIX]{x1D709}\unicode[STIX]{x1D708})$
.
$\unicode[STIX]{x1D6F1}(\text{H},\unicode[STIX]{x1D709}\unicode[STIX]{x1D708})$
.
Now suppose that
![]() $(\text{L}/\text{F},\unicode[STIX]{x1D709})$
has associated
$(\text{L}/\text{F},\unicode[STIX]{x1D709})$
has associated
![]() $1$
-pair
$1$
-pair
![]() $(\text{E}/\text{F},\unicode[STIX]{x1D709}_{0})$
and
$(\text{E}/\text{F},\unicode[STIX]{x1D709}_{0})$
and
![]() $\text{L}$
is contained in
$\text{L}$
is contained in
![]() $\overline{\text{F}}$
. Since
$\overline{\text{F}}$
. Since
![]() $\text{L}/\text{F}$
has degree
$\text{L}/\text{F}$
has degree
![]() $n$
and
$n$
and
![]() $\text{L}$
is unramified over
$\text{L}$
is unramified over
![]() $\text{E}$
, the residue field of
$\text{E}$
, the residue field of
![]() $\text{L}$
canonically identifies with
$\text{L}$
canonically identifies with
![]() $\boldsymbol{k}$
. We write
$\boldsymbol{k}$
. We write
![]() $\unicode[STIX]{x1D707}$
for the character of
$\unicode[STIX]{x1D707}$
for the character of
![]() $\boldsymbol{k}^{\times }$
induced by the restriction of
$\boldsymbol{k}^{\times }$
induced by the restriction of
![]() $\unicode[STIX]{x1D708}$
to the units subgroup of
$\unicode[STIX]{x1D708}$
to the units subgroup of
![]() $\text{L}$
. This character is entirely described by [Reference Bushnell and HenniartBH11a, Corollary 6.9], which gives us assertion (2) of the proposition.
$\text{L}$
. This character is entirely described by [Reference Bushnell and HenniartBH11a, Corollary 6.9], which gives us assertion (2) of the proposition.
Taking inertial classes and using Lemma 9.9, the Jacquet–Langlands correspondence matches together the inertial class
![]() $\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D6FC})$
of
$\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D6FC})$
of
![]() $\unicode[STIX]{x1D6F1}(\text{G},\unicode[STIX]{x1D709})$
with that of
$\unicode[STIX]{x1D6F1}(\text{G},\unicode[STIX]{x1D709})$
with that of
![]() $\unicode[STIX]{x1D6F1}(\text{H},\unicode[STIX]{x1D709}\unicode[STIX]{x1D708})$
, and the latter can be written as
$\unicode[STIX]{x1D6F1}(\text{H},\unicode[STIX]{x1D709}\unicode[STIX]{x1D708})$
, and the latter can be written as
![]() $\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D705}\text{sp}\prime ,\unicode[STIX]{x1D6FC}\text{sp}\prime )$
for
$\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D705}\text{sp}\prime ,\unicode[STIX]{x1D6FC}\text{sp}\prime )$
for
![]() $[\unicode[STIX]{x1D6FC}\text{sp}\prime ]=[\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D709}\unicode[STIX]{x1D708}}]=[\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D707}]$
. The result follows.◻
$[\unicode[STIX]{x1D6FC}\text{sp}\prime ]=[\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D709}\unicode[STIX]{x1D708}}]=[\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D707}]$
. The result follows.◻
9.5
We now prove Theorem 9.3. Following Remark 8.7, let us fix an odd integer
![]() $a\geqslant 7$
. We will see below why it is convenient to choose
$a\geqslant 7$
. We will see below why it is convenient to choose
![]() $a$
odd. We use the notation introduced in § 8.3. In particular, we have
$a$
odd. We use the notation introduced in § 8.3. In particular, we have
![]() $\unicode[STIX]{x1D6FD}$
-extensions
$\unicode[STIX]{x1D6FD}$
-extensions
![]() $\unicode[STIX]{x1D705}^{\ast }$
and
$\unicode[STIX]{x1D705}^{\ast }$
and
![]() $\unicode[STIX]{x1D705}^{\prime \ast }$
and a permutation
$\unicode[STIX]{x1D705}^{\prime \ast }$
and a permutation
![]() $\unicode[STIX]{x1D6F6}^{\ast }$
of
$\unicode[STIX]{x1D6F6}^{\ast }$
of
![]() $\text{X}^{\ast }/\unicode[STIX]{x1D6E4}^{\ast }$
. We must pay attention to the fact that the determinants of
$\text{X}^{\ast }/\unicode[STIX]{x1D6E4}^{\ast }$
. We must pay attention to the fact that the determinants of
![]() $\unicode[STIX]{x1D705}^{\ast }$
and
$\unicode[STIX]{x1D705}^{\ast }$
and
![]() $\unicode[STIX]{x1D705}^{\prime \ast }$
have orders which may not be powers of
$\unicode[STIX]{x1D705}^{\prime \ast }$
have orders which may not be powers of
![]() $p$
, so Proposition 9.10 may not apply to
$p$
, so Proposition 9.10 may not apply to
![]() $\unicode[STIX]{x1D6F6}^{\ast }$
directly.
$\unicode[STIX]{x1D6F6}^{\ast }$
directly.
Let us write
![]() $\unicode[STIX]{x1D705}_{p}^{\ast }$
for the
$\unicode[STIX]{x1D705}_{p}^{\ast }$
for the
![]() $\unicode[STIX]{x1D6FD}$
-extension on
$\unicode[STIX]{x1D6FD}$
-extension on
![]() $\text{J}(\mathfrak{a}^{\ast },\unicode[STIX]{x1D704}\unicode[STIX]{x1D6FD})$
whose determinant has order a power of
$\text{J}(\mathfrak{a}^{\ast },\unicode[STIX]{x1D704}\unicode[STIX]{x1D6FD})$
whose determinant has order a power of
![]() $p$
. By Remark 3.11 there is a character
$p$
. By Remark 3.11 there is a character
![]() $\unicode[STIX]{x1D701}$
of
$\unicode[STIX]{x1D701}$
of
![]() $\text{J}(\mathfrak{a}^{\ast },\unicode[STIX]{x1D704}\unicode[STIX]{x1D6FD})$
trivial on
$\text{J}(\mathfrak{a}^{\ast },\unicode[STIX]{x1D704}\unicode[STIX]{x1D6FD})$
trivial on
![]() $\text{J}^{1}(\mathfrak{a}^{\ast },\unicode[STIX]{x1D704}\unicode[STIX]{x1D6FD})$
such that
$\text{J}^{1}(\mathfrak{a}^{\ast },\unicode[STIX]{x1D704}\unicode[STIX]{x1D6FD})$
such that
![]() $\unicode[STIX]{x1D705}_{p}^{\ast }=\unicode[STIX]{x1D705}^{\ast }\unicode[STIX]{x1D701}$
. This induces a character of
$\unicode[STIX]{x1D705}_{p}^{\ast }=\unicode[STIX]{x1D705}^{\ast }\unicode[STIX]{x1D701}$
. This induces a character of
![]() $\text{GL}_{m\text{sp}\prime }(\boldsymbol{d})$
of the form
$\text{GL}_{m\text{sp}\prime }(\boldsymbol{d})$
of the form
![]() $\unicode[STIX]{x1D712}\circ \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D704}}\circ \text{N}_{\boldsymbol{d}/\boldsymbol{e}_{\unicode[STIX]{x1D704}}}\circ \det$
for some character
$\unicode[STIX]{x1D712}\circ \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D704}}\circ \text{N}_{\boldsymbol{d}/\boldsymbol{e}_{\unicode[STIX]{x1D704}}}\circ \det$
for some character
![]() $\unicode[STIX]{x1D712}$
of
$\unicode[STIX]{x1D712}$
of
![]() $\boldsymbol{e}^{\times }$
.
$\boldsymbol{e}^{\times }$
.
Similarly, we have a
![]() $\unicode[STIX]{x1D6FD}$
-extension
$\unicode[STIX]{x1D6FD}$
-extension
![]() $\unicode[STIX]{x1D705}_{p}^{\prime \ast }$
whose determinant has order a power of
$\unicode[STIX]{x1D705}_{p}^{\prime \ast }$
whose determinant has order a power of
![]() $p$
, as well as characters
$p$
, as well as characters
![]() $\unicode[STIX]{x1D701}\text{sp}\prime$
and
$\unicode[STIX]{x1D701}\text{sp}\prime$
and
![]() $\unicode[STIX]{x1D712}\text{sp}\prime$
such that
$\unicode[STIX]{x1D712}\text{sp}\prime$
such that
![]() $\unicode[STIX]{x1D705}_{p}^{\prime \ast }=\unicode[STIX]{x1D705}^{\prime \ast }\unicode[STIX]{x1D701}\text{sp}\prime$
and
$\unicode[STIX]{x1D705}_{p}^{\prime \ast }=\unicode[STIX]{x1D705}^{\prime \ast }\unicode[STIX]{x1D701}\text{sp}\prime$
and
![]() $\unicode[STIX]{x1D701}\text{sp}\prime$
induces the character
$\unicode[STIX]{x1D701}\text{sp}\prime$
induces the character
![]() $\unicode[STIX]{x1D712}\text{sp}\prime \circ \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D704}\text{sp}\prime }\circ \det$
of
$\unicode[STIX]{x1D712}\text{sp}\prime \circ \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D704}\text{sp}\prime }\circ \det$
of
![]() $\text{GL}_{n\text{sp}\prime }(\boldsymbol{e}_{\unicode[STIX]{x1D704}\text{sp}\prime })$
. We write
$\text{GL}_{n\text{sp}\prime }(\boldsymbol{e}_{\unicode[STIX]{x1D704}\text{sp}\prime })$
. We write
![]() $\unicode[STIX]{x1D6F9}_{p}$
for the permutation of
$\unicode[STIX]{x1D6F9}_{p}$
for the permutation of
![]() $\text{X}^{\ast }/\unicode[STIX]{x1D6E4}^{\ast }$
corresponding to the maximal
$\text{X}^{\ast }/\unicode[STIX]{x1D6E4}^{\ast }$
corresponding to the maximal
![]() $\unicode[STIX]{x1D6FD}$
-extensions
$\unicode[STIX]{x1D6FD}$
-extensions
![]() $\unicode[STIX]{x1D705}_{p}^{\ast }$
and
$\unicode[STIX]{x1D705}_{p}^{\ast }$
and
![]() $\unicode[STIX]{x1D705}_{p}^{\prime \ast }$
. We write
$\unicode[STIX]{x1D705}_{p}^{\prime \ast }$
. We write
![]() $\unicode[STIX]{x1D6FF}$
for the character
$\unicode[STIX]{x1D6FF}$
for the character
![]() $(\unicode[STIX]{x1D712}\text{sp}\prime \unicode[STIX]{x1D712}^{-1})\circ \text{N}_{\boldsymbol{k}^{\ast }/\boldsymbol{e}}\in \text{X}^{\ast }$
.
$(\unicode[STIX]{x1D712}\text{sp}\prime \unicode[STIX]{x1D712}^{-1})\circ \text{N}_{\boldsymbol{k}^{\ast }/\boldsymbol{e}}\in \text{X}^{\ast }$
.
Lemma 9.11. The character
![]() $\unicode[STIX]{x1D6FF}$
is trivial.
$\unicode[STIX]{x1D6FF}$
is trivial.
Proof. Let
![]() $\unicode[STIX]{x1D6FD}\in \text{X}^{\ast }$
be an
$\unicode[STIX]{x1D6FD}\in \text{X}^{\ast }$
be an
![]() $\boldsymbol{e}$
-regular character. Applying Proposition 9.10 to
$\boldsymbol{e}$
-regular character. Applying Proposition 9.10 to
![]() $\unicode[STIX]{x1D6F9}_{p}$
gives us the equality
$\unicode[STIX]{x1D6F9}_{p}$
gives us the equality
![]() $\unicode[STIX]{x1D6F9}_{p}([\unicode[STIX]{x1D6FD}])=[\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D706}]$
where
$\unicode[STIX]{x1D6F9}_{p}([\unicode[STIX]{x1D6FD}])=[\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D706}]$
where
![]() $\unicode[STIX]{x1D706}\in \text{X}^{\ast }$
is the rectifying character corresponding to
$\unicode[STIX]{x1D706}\in \text{X}^{\ast }$
is the rectifying character corresponding to
![]() $am$
,
$am$
,
![]() $d$
and
$d$
and
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
. Since
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
. Since
![]() $a$
has been chosen to be odd, we have
$a$
has been chosen to be odd, we have
It follows that
![]() $\unicode[STIX]{x1D706}$
is trivial if and only if
$\unicode[STIX]{x1D706}$
is trivial if and only if
![]() $\unicode[STIX]{x1D707}$
is, that is,
$\unicode[STIX]{x1D707}$
is, that is,
![]() $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D707}^{\ast }$
. We thus get
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D707}^{\ast }$
. We thus get
![]() $\unicode[STIX]{x1D6F9}_{p}([\unicode[STIX]{x1D6FD}])=[\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D707}^{\ast }]$
.
$\unicode[STIX]{x1D6F9}_{p}([\unicode[STIX]{x1D6FD}])=[\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D707}^{\ast }]$
.
Now let
![]() $\unicode[STIX]{x1D700}$
be the character
$\unicode[STIX]{x1D700}$
be the character
![]() $\unicode[STIX]{x1D712}\circ \text{N}_{\boldsymbol{k}^{\ast }/\boldsymbol{e}}$
and define
$\unicode[STIX]{x1D712}\circ \text{N}_{\boldsymbol{k}^{\ast }/\boldsymbol{e}}$
and define
![]() $\unicode[STIX]{x1D700}\text{sp}\prime$
similarly. Comparing
$\unicode[STIX]{x1D700}\text{sp}\prime$
similarly. Comparing
![]() $\unicode[STIX]{x1D6F9}_{p}$
and
$\unicode[STIX]{x1D6F9}_{p}$
and
![]() $\unicode[STIX]{x1D6F6}^{\ast }$
, by Remark 3.11 we get
$\unicode[STIX]{x1D6F6}^{\ast }$
, by Remark 3.11 we get
![]() $\unicode[STIX]{x1D6F6}^{\ast }([\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D700}])=[\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D707}^{\ast }\unicode[STIX]{x1D700}\text{sp}\prime ]$
for all
$\unicode[STIX]{x1D6F6}^{\ast }([\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D700}])=[\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D707}^{\ast }\unicode[STIX]{x1D700}\text{sp}\prime ]$
for all
![]() $\boldsymbol{e}$
-regular character
$\boldsymbol{e}$
-regular character
![]() $\unicode[STIX]{x1D6FD}\in \text{X}^{\ast }$
. Since
$\unicode[STIX]{x1D6FD}\in \text{X}^{\ast }$
. Since
![]() $\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D700}^{-1}$
is
$\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D700}^{-1}$
is
![]() $\boldsymbol{e}$
-regular if and only if
$\boldsymbol{e}$
-regular if and only if
![]() $\unicode[STIX]{x1D6FD}$
is, this gives us
$\unicode[STIX]{x1D6FD}$
is, this gives us
for all
![]() $\boldsymbol{e}$
-regular
$\boldsymbol{e}$
-regular
![]() $\unicode[STIX]{x1D6FD}\in \text{X}^{\ast }$
.
$\unicode[STIX]{x1D6FD}\in \text{X}^{\ast }$
.
Now let
![]() $\unicode[STIX]{x1D6FC}\in \text{X}_{\text{reg}}$
. By Lemma 8.5 there are a prime number
$\unicode[STIX]{x1D6FC}\in \text{X}_{\text{reg}}$
. By Lemma 8.5 there are a prime number
![]() $\ell \neq p$
not dividing the order of
$\ell \neq p$
not dividing the order of
![]() $\boldsymbol{k}^{\times }$
and an
$\boldsymbol{k}^{\times }$
and an
![]() $\boldsymbol{e}$
-regular character
$\boldsymbol{e}$
-regular character
![]() $\unicode[STIX]{x1D6FD}\in \text{X}^{\ast }$
such that
$\unicode[STIX]{x1D6FD}\in \text{X}^{\ast }$
such that
![]() $\unicode[STIX]{x1D6FD}\equiv \unicode[STIX]{x1D6FC}^{\ast }$
mod
$\unicode[STIX]{x1D6FD}\equiv \unicode[STIX]{x1D6FC}^{\ast }$
mod
![]() $\ell$
. By (9.5) and Proposition 8.8 we get
$\ell$
. By (9.5) and Proposition 8.8 we get
![]() $\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FC}])=[\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D708}]$
for some
$\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FC}])=[\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D708}]$
for some
![]() $\unicode[STIX]{x1D708}\in \text{X}$
such that
$\unicode[STIX]{x1D708}\in \text{X}$
such that
![]() $\unicode[STIX]{x1D708}^{\ast }$
is the
$\unicode[STIX]{x1D708}^{\ast }$
is the
![]() $\ell$
-regular part of
$\ell$
-regular part of
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D707}^{\ast }$
. Since
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D707}^{\ast }$
. Since
![]() $\unicode[STIX]{x1D6FC}$
is
$\unicode[STIX]{x1D6FC}$
is
![]() $\boldsymbol{e}$
-regular, Proposition 9.10 applied to
$\boldsymbol{e}$
-regular, Proposition 9.10 applied to
![]() $\unicode[STIX]{x1D6F6}$
gives us
$\unicode[STIX]{x1D6F6}$
gives us
![]() $\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FC}])=[\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D707}]$
. Putting these equalities together, we get
$\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FC}])=[\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D707}]$
. Putting these equalities together, we get
The character
![]() $\unicode[STIX]{x1D6FF}$
can thus be written as
$\unicode[STIX]{x1D6FF}$
can thus be written as
![]() $\unicode[STIX]{x1D709}(\unicode[STIX]{x1D6FC}^{\ast }\unicode[STIX]{x1D707}^{\ast })^{\text{Q}^{i}-1}$
for some integer
$\unicode[STIX]{x1D709}(\unicode[STIX]{x1D6FC}^{\ast }\unicode[STIX]{x1D707}^{\ast })^{\text{Q}^{i}-1}$
for some integer
![]() $i\in \{0,\ldots ,n\text{sp}\prime -1\}$
and some
$i\in \{0,\ldots ,n\text{sp}\prime -1\}$
and some
![]() $\unicode[STIX]{x1D709}\in \text{X}^{\ast }$
whose order is a power of
$\unicode[STIX]{x1D709}\in \text{X}^{\ast }$
whose order is a power of
![]() $\ell$
. (Recall that
$\ell$
. (Recall that
![]() $\text{Q}$
is the cardinality of
$\text{Q}$
is the cardinality of
![]() $\boldsymbol{e}$
.) Since
$\boldsymbol{e}$
.) Since
![]() $\unicode[STIX]{x1D707}$
has order at most
$\unicode[STIX]{x1D707}$
has order at most
![]() $2$
, we get
$2$
, we get
![]() $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D709}(\unicode[STIX]{x1D6FC}^{\ast })^{\text{Q}^{i}-1}$
. Since the orders of
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D709}(\unicode[STIX]{x1D6FC}^{\ast })^{\text{Q}^{i}-1}$
. Since the orders of
![]() $\unicode[STIX]{x1D6FF}$
and
$\unicode[STIX]{x1D6FF}$
and
![]() $\unicode[STIX]{x1D707}^{\ast }$
both divide
$\unicode[STIX]{x1D707}^{\ast }$
both divide
![]() $\text{Q}-1$
, we have
$\text{Q}-1$
, we have
Since both
![]() $\text{Q}-1$
and the order of
$\text{Q}-1$
and the order of
![]() $\unicode[STIX]{x1D6FC}$
are prime to
$\unicode[STIX]{x1D6FC}$
are prime to
![]() $\ell$
, we get
$\ell$
, we get
![]() $\unicode[STIX]{x1D709}=1$
. Hence the order of
$\unicode[STIX]{x1D709}=1$
. Hence the order of
![]() $\unicode[STIX]{x1D6FC}$
, which we may assume to be
$\unicode[STIX]{x1D6FC}$
, which we may assume to be
![]() $\text{Q}^{n\text{sp}\prime }-1$
by choosing for
$\text{Q}^{n\text{sp}\prime }-1$
by choosing for
![]() $\unicode[STIX]{x1D6FC}$
a generator of
$\unicode[STIX]{x1D6FC}$
a generator of
![]() $\text{X}$
, divides
$\text{X}$
, divides
![]() $(\text{Q}^{i}-1)(\text{Q}-1)$
. This implies
$(\text{Q}^{i}-1)(\text{Q}-1)$
. This implies
![]() $i=0$
, so
$i=0$
, so
![]() $\unicode[STIX]{x1D6FF}$
is trivial as expected.◻
$\unicode[STIX]{x1D6FF}$
is trivial as expected.◻
Now let
![]() $\unicode[STIX]{x1D6FC}\in \text{X}$
be arbitrary. By Lemma 8.5 there are a prime number
$\unicode[STIX]{x1D6FC}\in \text{X}$
be arbitrary. By Lemma 8.5 there are a prime number
![]() $\ell \neq p$
not dividing the order of
$\ell \neq p$
not dividing the order of
![]() $\boldsymbol{e}[\unicode[STIX]{x1D6FC}]^{\times }$
and an
$\boldsymbol{e}[\unicode[STIX]{x1D6FC}]^{\times }$
and an
![]() $\boldsymbol{e}$
-regular character
$\boldsymbol{e}$
-regular character
![]() $\unicode[STIX]{x1D6FD}\in \text{X}^{\ast }$
such that
$\unicode[STIX]{x1D6FD}\in \text{X}^{\ast }$
such that
![]() $\unicode[STIX]{x1D6FD}$
is congruent to
$\unicode[STIX]{x1D6FD}$
is congruent to
![]() $\unicode[STIX]{x1D6FC}^{\ast }$
mod
$\unicode[STIX]{x1D6FC}^{\ast }$
mod
![]() $\ell$
. Since
$\ell$
. Since
![]() $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D707}^{\ast }$
, the identity (9.5) gives us
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D707}^{\ast }$
, the identity (9.5) gives us
![]() $\unicode[STIX]{x1D6F6}^{\ast }([\unicode[STIX]{x1D6FD}])=[\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D707}^{\ast }]$
. By Proposition 8.8, we have
$\unicode[STIX]{x1D6F6}^{\ast }([\unicode[STIX]{x1D6FD}])=[\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D707}^{\ast }]$
. By Proposition 8.8, we have
![]() $\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FC}])=[\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D708}]$
for some character
$\unicode[STIX]{x1D6F6}([\unicode[STIX]{x1D6FC}])=[\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D708}]$
for some character
![]() $\unicode[STIX]{x1D708}\in \text{X}$
such that
$\unicode[STIX]{x1D708}\in \text{X}$
such that
![]() $\unicode[STIX]{x1D708}^{\ast }$
is the
$\unicode[STIX]{x1D708}^{\ast }$
is the
![]() $\ell$
-regular part of
$\ell$
-regular part of
![]() $\unicode[STIX]{x1D707}^{\ast }$
. Thus
$\unicode[STIX]{x1D707}^{\ast }$
. Thus
![]() $\unicode[STIX]{x1D708}^{\ast }=\unicode[STIX]{x1D707}^{\ast }$
, which implies
$\unicode[STIX]{x1D708}^{\ast }=\unicode[STIX]{x1D707}^{\ast }$
, which implies
![]() $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D707}$
. This completes the proof of Theorem 9.3.
$\unicode[STIX]{x1D708}=\unicode[STIX]{x1D707}$
. This completes the proof of Theorem 9.3.
Corollary 9.12. The permutation
![]() $\unicode[STIX]{x1D6F6}$
does not depend on the choice of the
$\unicode[STIX]{x1D6F6}$
does not depend on the choice of the
![]() $\text{F}$
-embeddings
$\text{F}$
-embeddings
![]() $\unicode[STIX]{x1D704}$
and
$\unicode[STIX]{x1D704}$
and
![]() $\unicode[STIX]{x1D704}\text{sp}\prime$
and the orders
$\unicode[STIX]{x1D704}\text{sp}\prime$
and the orders
![]() $\mathfrak{a}$
and
$\mathfrak{a}$
and
![]() $\mathfrak{a}\text{sp}\prime$
, nor on the choice of the ps-character
$\mathfrak{a}\text{sp}\prime$
, nor on the choice of the ps-character
![]() $(\unicode[STIX]{x1D6E9},0,\unicode[STIX]{x1D6FD})$
of endo-class
$(\unicode[STIX]{x1D6E9},0,\unicode[STIX]{x1D6FD})$
of endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
.
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
.
9.6
We now reformulate Theorem 9.3 in terms of admissible pairs. Let
![]() $(\text{L}/\text{F},\unicode[STIX]{x1D709})$
be an admissible pair of degree dividing
$(\text{L}/\text{F},\unicode[STIX]{x1D709})$
be an admissible pair of degree dividing
![]() $n$
and endo-class
$n$
and endo-class
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
. The orbit
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
. The orbit
![]() $[\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D709}}]\in \text{X}/\unicode[STIX]{x1D6E4}$
given by (9.3) corresponds through (9.1) to an inertial class
$[\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D709}}]\in \text{X}/\unicode[STIX]{x1D6E4}$
given by (9.3) corresponds through (9.1) to an inertial class
![]() $\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D709}})$
of discrete series representations. Write
$\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D709}})$
of discrete series representations. Write
![]() $\unicode[STIX]{x1D6F1}_{0}(\text{G},\unicode[STIX]{x1D709})$
for this inertial class. The map
$\unicode[STIX]{x1D6F1}_{0}(\text{G},\unicode[STIX]{x1D709})$
for this inertial class. The map
is a bijection between
![]() $\mathscr{P}_{n}(\boldsymbol{\unicode[STIX]{x1D6E9}})$
and
$\mathscr{P}_{n}(\boldsymbol{\unicode[STIX]{x1D6E9}})$
and
![]() $\mathscr{D}_{0}(\text{G},\boldsymbol{\unicode[STIX]{x1D6E9}})$
. This map depends a priori on various choices.
$\mathscr{D}_{0}(\text{G},\boldsymbol{\unicode[STIX]{x1D6E9}})$
. This map depends a priori on various choices.
Theorem 9.13. Let
![]() $(\text{L}/\text{F},\unicode[STIX]{x1D709})$
be an admissible pair with degree dividing
$(\text{L}/\text{F},\unicode[STIX]{x1D709})$
be an admissible pair with degree dividing
![]() $n$
. There is a canonically determined tamely ramified character
$n$
. There is a canonically determined tamely ramified character
![]() $\unicode[STIX]{x1D707}$
of the units subgroup of
$\unicode[STIX]{x1D707}$
of the units subgroup of
![]() $\text{L}$
such that
$\text{L}$
such that
![]() $\unicode[STIX]{x1D707}^{2}=1$
and
$\unicode[STIX]{x1D707}^{2}=1$
and
It depends only on
![]() $m$
,
$m$
,
![]() $d$
and the restriction of
$d$
and the restriction of
![]() $\unicode[STIX]{x1D709}$
to the principal units
$\unicode[STIX]{x1D709}$
to the principal units
![]() $1+\mathfrak{p}_{\text{L}}$
.
$1+\mathfrak{p}_{\text{L}}$
.
Note that by
![]() $\unicode[STIX]{x1D6F1}_{0}(\text{H},\unicode[STIX]{x1D709}\unicode[STIX]{x1D707})$
we mean the inertial class corresponding to the pair
$\unicode[STIX]{x1D6F1}_{0}(\text{H},\unicode[STIX]{x1D709}\unicode[STIX]{x1D707})$
we mean the inertial class corresponding to the pair
![]() $[\text{L}/\text{F},\unicode[STIX]{x1D709}\hat{\unicode[STIX]{x1D707}}]$
for any choice of extension
$[\text{L}/\text{F},\unicode[STIX]{x1D709}\hat{\unicode[STIX]{x1D707}}]$
for any choice of extension
![]() $\hat{\unicode[STIX]{x1D707}}$
of
$\hat{\unicode[STIX]{x1D707}}$
of
![]() $\unicode[STIX]{x1D707}$
to
$\unicode[STIX]{x1D707}$
to
![]() $\text{L}^{\times }$
; this is independent of the choice of
$\text{L}^{\times }$
; this is independent of the choice of
![]() $\hat{\unicode[STIX]{x1D707}}$
.
$\hat{\unicode[STIX]{x1D707}}$
.
Remark 9.14. Let
![]() $t$
be the degree of
$t$
be the degree of
![]() $\text{L}/\text{F}$
and write
$\text{L}/\text{F}$
and write
![]() $s$
for the integer
$s$
for the integer
![]() $s(\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D709}})$
defined by (8.3). The parametric degree
$s(\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D709}})$
defined by (8.3). The parametric degree
![]() $f=[\text{L}:\text{E}]$
of
$f=[\text{L}:\text{E}]$
of
![]() $\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D709}}$
divides
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D709}}$
divides
![]() $m\text{sp}\prime d\text{sp}\prime$
. Therefore
$m\text{sp}\prime d\text{sp}\prime$
. Therefore
![]() $u=f/(f,d\text{sp}\prime )$
divides
$u=f/(f,d\text{sp}\prime )$
divides
![]() $m\text{sp}\prime s$
and hence
$m\text{sp}\prime s$
and hence
![]() $m\text{sp}\prime$
. Let us define an integer
$m\text{sp}\prime$
. Let us define an integer
![]() $r\geqslant 1$
by
$r\geqslant 1$
by
![]() $m\text{sp}\prime =ur$
, or equivalently by
$m\text{sp}\prime =ur$
, or equivalently by
![]() $n=rst$
. Any discrete series representation in
$n=rst$
. Any discrete series representation in
![]() $\unicode[STIX]{x1D6F1}_{0}(\text{G},\unicode[STIX]{x1D709})$
has the form
$\unicode[STIX]{x1D6F1}_{0}(\text{G},\unicode[STIX]{x1D709})$
has the form
![]() $\text{L}(\unicode[STIX]{x1D70C},r)$
for some cuspidal representation
$\text{L}(\unicode[STIX]{x1D70C},r)$
for some cuspidal representation
![]() $\unicode[STIX]{x1D70C}$
of
$\unicode[STIX]{x1D70C}$
of
![]() $\text{GL}_{m/r}(\text{D})$
with parametric degree
$\text{GL}_{m/r}(\text{D})$
with parametric degree
![]() $t$
.
$t$
.
Remark 9.15. An admissible pair
![]() $(\text{L}/\text{F},\unicode[STIX]{x1D709})$
of degree
$(\text{L}/\text{F},\unicode[STIX]{x1D709})$
of degree
![]() $t$
dividing
$t$
dividing
![]() $n$
canonically defines, via the canonical map (9.4), an isomorphism class of essentially tame cuspidal representations
$n$
canonically defines, via the canonical map (9.4), an isomorphism class of essentially tame cuspidal representations
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D709}}$
of the group
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D709}}$
of the group
![]() $\text{GL}_{t}(\text{F})$
. Passing to inertial classes, the map
$\text{GL}_{t}(\text{F})$
. Passing to inertial classes, the map
induces the map (9.6) when
![]() $\text{G}=\text{H}$
, which is therefore canonical in that case. It follows from Theorem 9.13 that (9.6) is a canonical bijection between
$\text{G}=\text{H}$
, which is therefore canonical in that case. It follows from Theorem 9.13 that (9.6) is a canonical bijection between
![]() $\mathscr{P}_{n}(\boldsymbol{\unicode[STIX]{x1D6E9}})$
and
$\mathscr{P}_{n}(\boldsymbol{\unicode[STIX]{x1D6E9}})$
and
![]() $\mathscr{D}_{0}(\text{G},\boldsymbol{\unicode[STIX]{x1D6E9}})$
, for any inner form
$\mathscr{D}_{0}(\text{G},\boldsymbol{\unicode[STIX]{x1D6E9}})$
, for any inner form
![]() $\text{G}$
.
$\text{G}$
.
Acknowledgements
The research of the second author was supported by the Engineering and Physical Sciences Research Council (grant EP/H00534X/1). We thank the anonymous referee for several useful comments, particularly relating to the presentation in § 6.