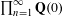We define and study new categories of ‘pre $C^\infty$-rings with corners’ and ‘ $C^\infty$-rings with corners’. These are pairs (C,C_{ex}) of sets with many algebraic operations. If X is a manifold with corners then taking C to be the set of smooth maps X -> R, and C_{ex} the set of smooth maps X -> [0,infinity), gives a $C^\infty$-ring with corners. It helps to consider C a $C^\infty$-ring or R-algebra, and C_{ex} a commutative monoid which adds ‘corner structure’ to C.
A (pre) $C^\infty$-ring with corners can equivalently defined as a product-preserving functor from the category of Euclidean spaces with corners [0,infinity)^k x R^{n-k} to the category of sets. This is an example of an Algebraic Theory, so theorems from Algebraic Theories apply.
We define interesting subcategories of $C^\infty$-rings with corners with special properties - interior, firm, toric, ... and study their categorical properties, e.g. existence of (co)limits.
Much of the theory of commutative algebras and $C^\infty$-rings used in scheme theory extends to $C^\infty$-rings with corners, e.g. local $C^\infty$-rings with corners and localization, free $C^\infty$-rings with corners, generators, and relations.